Математическая модель турбулентного течения с переносом примеси
Конференция: XCII Студенческая международная научно-практическая конференция «Молодежный научный форум»
Секция: Физико-математические науки
лауреатов
участников
лауреатов


участников



XCII Студенческая международная научно-практическая конференция «Молодежный научный форум»
Математическая модель турбулентного течения с переносом примеси
MATHEMATICAL MODEL OF A TURBULENT FLOW WITH PARTICLE TRANSPORT
Alexandra Makhmutova
Student, Ufa state aviation technical University, Russia, Ufa
Аннотация. Целью работы было создание математической модели течения жидкости с переносом частиц. Метод: для моделирования течения были взяты уравнения Рейнольдса с приближением Буссинеска, высокорейнольдсовая k-ε модель, записаны уравнения переноса инертной примеси. Результат: построенная модель готова к реализации в виде программного продукта для численного моделирования двумерной задачи в сечении трубы. Выводы: данная k-ε модель является одним из вариантов моделирования турбулентности и послужит прототипом для моделей, основанных на более простых корреляциях.
Abstract. Background. The aim of the work was to create a mathematical model of liquid flow with particle transfer. Method: The Reynolds equations with Boussinesk approximation and the high Reynolds k-ε model were taken to model the flow, the inert impurity transfer equations were written down. Result: the constructed model is ready for realization in the form of a software product for numerical modeling of a two-dimensional problem in a pipe section. Conclusion: this k-ε model is one of the options of modeling turbulence and will be used as a prototype for models based on simpler correlations.
Ключевые слова: модель турбулентности; перенос примеси; k-ε модель.
Keywords: turbulent model; particle diffusivity; k-ε model.
В настоящий момент создано большое количество разнообразных моделей для расчёта турбулентных течений. Они отличаются друг от друга сложностью решения и точностью описания течения. Мы провели сравнение разновидностей и модификаций k-epsilon моделей, чтобы выбрать подходящую для нашего случая. При этом необязательно выбирать самые модифицированные версии, если в этом нет необходимости, ведь из-за этого может пострадать вычислительная скорость.
Известно, что в нашем случае предполагается безотрывное течение без вихрей и деформаций. Течение турбулентно – расчётное число Рейнольдса получилось более 50 000. Соответственно, наиболее подходящая для данной задачи модель – стандартная высокорейнольдсовая k-ɛ модель с пристеночными функциями.
Запишем систему уравнений Рейнольдса: молекулярная вязкость отсутствует, так как она настолько мала, что ею можно пренебречь. Исключаем производные по координате X (вдоль трубы), так как рассматриваем поперечное сечение:
![]()
![]() (1)
(1)
![]()
![]()
где ![]() – турбулентная вязкость;
– турбулентная вязкость;
u, v, w – компоненты скорости смеси.
Уравнения для ![]() :
:
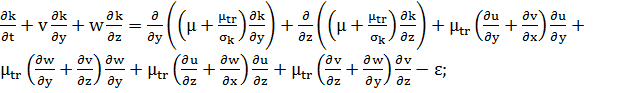 (2)
(2)
 (3)
(3)
Теперь запишем уравнения для плотности и добавим в уравнения движения смеси приближение Буссинеска.
![]() (4)
(4)
![]() (5)
(5)
где коэффициент объемного расширения жидкости ![]() .
.
Уравнение переноса инертной примеси:
![]() (6)
(6)
где ![]() – коэффициент диффузии,
– коэффициент диффузии, ![]() , где
, где ![]() – турбулентное число Шмидта, скорости – объемные скорости переноса примеси.
– турбулентное число Шмидта, скорости – объемные скорости переноса примеси.
Скорость оседания одиночной частицы взята по Eskin [1]:

где ![]() – диаметр частицы;
– диаметр частицы;
![]() – коэффициент лобового сопротивления частицы;
– коэффициент лобового сопротивления частицы;
![]() – отношение плотности частицы к плотности жидкости.
– отношение плотности частицы к плотности жидкости.
В результате мы получили систему уравнений для моделирования течения жидкости с частицами. Полученная модель готова к реализации в виде программного продукта для численного моделирования двумерной задачи в сечении трубы. Данная k-ε модель является одним из вариантов моделирования турбулентности и послужит прототипом для моделей, основанных на более простых корреляциях.

