ОЦЕНКА ОПТИМАЛЬНЫХ ЗНАЧЕНИЙ ФАКТОРОВ ПРОИЗВОДСТВА (ПРОИЗВОДСТВЕННОЙ ФУНКЦИИ КОББА – ДУГЛАСА) В ДУОПОЛИИ РЫНКА ПО МОДЕЛИ КУРНО

Цель работы. Изучить равновесие Неша олигополистов в условии дуополии Курно.

Введение. Определение модели: Пусть на рынке действует дуополия с объемами поставок продукции q1,q₂ такие что:

Где:

 факторы производства

a₁,a₂,a₃…a_n b₁,b₂,b₃…b_n  - эластичность объема продукции по фактору производства

(объем представлен в виде модели Кобба–Дугласа предполагается что для производства некоторого объема продукции для обеих фирм действуют одинаковые факторы производства, ниже приведём модель дуополии с различными факторами производства) и функциями издержек TC1(q1 ) = TC2 (q2 ) , такие что

TC_m=

Где: Pi – это есть цена на использование некоторого фактора;

Xi – это фактор производства.

 Отраслевой спрос задан некоторой функцией  Спрос есть линейна функция.

Результаты исследования.

Тогда максимальная выручка каждой фирмы, для каждого дуополиста достигнет тогда, когда они будут использовать факторы производства пропорционально критическим точкам следующего уравнения условного экстремума:

TC₁- )     

L – коэффициент Лагранжа;

F – функция условного экстремума.

Найдём частные производные для относительно , (чтобы облегчить решение нахождения критических точек, мы заменили функцию ввида   натуральным логарифмом функции  F*=     то есть перевели  .

Ниже получаем следующую систему;

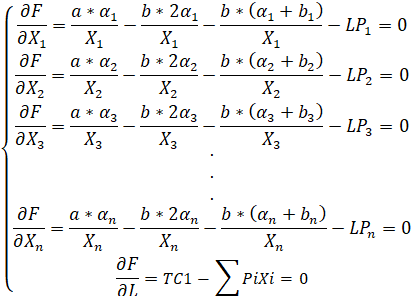
Решая данную систему получаем следующее решение для ;

=

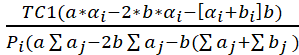
Где a_i ,b_i=есть эластичность факторов производства  q₁

Замечание : Мы предприняли функцию   как функцию F*=    по причине того что обе функции являются монотонно –возрастающими  и дифференцируемыми .

В условиях равенства эластичностей для двух олигополистов (a_i = b_i), равновесием будет точка касания изокванты к изокосте. Заметим одну интересную особенность, при различных значениях эластичностей, наблюдается смещение обеих изоквант в левую сторону, относительно изокосты.

И точкой равновесия будет точка пересечения, изокосты с изоквантой. Глубокое изучение поведения данной модели, является предметом дальнейших исследований.