Приближение произвольной функции классическим и модифицированным оператором sinc-аппроксимаций

Аннотация. Данная сатья посвящена изучению аппроксимативных свойств sinc-приближений, классических и модифицированных sinc-аппроксимаций непрерывной на отрезке функции.

Суть эксперимента

Впервые sinc-приближения появились в работах Плэйна в качестве инструмента приближённого вычисления корней многочленов.

Позднее, в связи с необходимостью развития теории кодирования сигналов, Э. Борель и Е. Т. Уиттекер ввели понятие кардинальной функции, сужение с оси на отрезке [0,π], которая выглядит так:

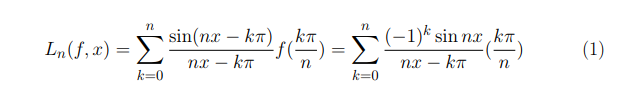
К настоящему времени достаточно фундаментально исследована проблема sinc -аппроксимации аналитической в полосе, содержащей действительную ось функции, экспоненциально убывающей на бесконечности.

Для проведения эксперимента необходимо ознакомиться с исследованиями аппроксимативных свойств операторов типа Лагранжа, построенных по решениям задачи Коши с дифференциальными уравнениями второго порядка и ставящих в соответствие любой, определённой на отрезке [0, π] функции f, непрерывную функцию таким образом:

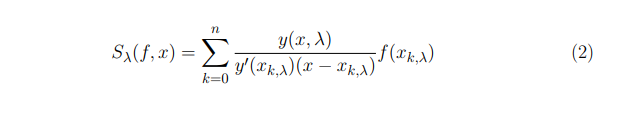
Подбирая соответствующим образом функции qλ, получается единое представление в виде данного оператора различных конструкций Лагранжева типа, таких как классические интерполяционные многочлены, кардинальные функции Уиттеккера, интерполяционные процессы Лагранжа. Если взять q_λ ≡ 0, λ_n = n², ℎ(λ_n) = n, то операторы в случае задачи Коши превращаются в усечённые кардинальные функции Уиттекера. Поэтому в численных экспериментах в качестве функций y(x, λ) будем брать sin nx.

Приближать произвольную функцию будем классическим оператором sinc-аппроксимаций и модифицированным оператором типа Лагранжа. Реализация будет прослеживаться на графике.

Приближаемая функция выглядит следующим образом:

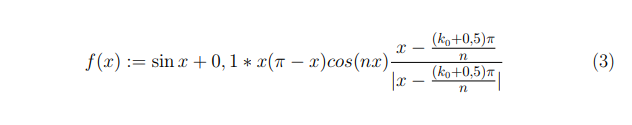
Оператор выглядит так:

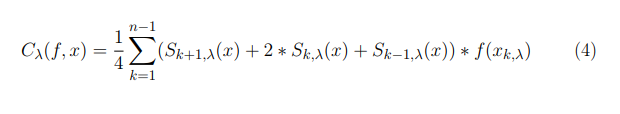
Численный эксперимент

Выполнение построения графика производится с помощью ПО MATLAB. MATLAB- это пакет прикладных программ для решения задач, технических вычислений и одноимённый язык программирования, используемый в этом пакете.

В работе приводится график, представленный на рисунке.

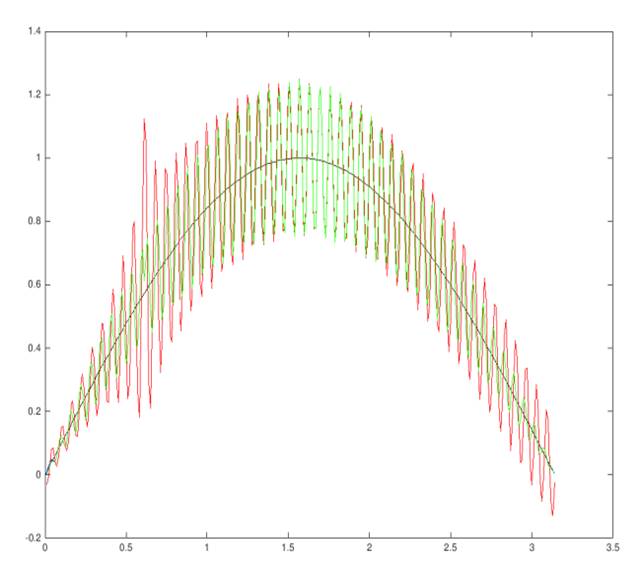
Рисунок. График численного эксперимента

В соответствии с рисунком, чёрным цветом изображён график численной реализации функции sin x на отрезке [0, π]; синим цветом изображён график по данным с помехами. В качестве приближаемой использована функция (3). На данной функции классические sinc-аппроксимации дают всплеск; у модифицированных операторов такого не происходит. Красным цветом изображён график приближения с помощью классических sinc-аппроксимаций (1). Также изображён график зелёного цвета, реализованный  с помощью заданного оператора (4). Оба оператора рассмотрены для n=100. С ростом n всплеск погрешности в районе узла под номером k₀=19 для sinc-аппроксимаций (1) будет расти как ln n, в то время как оператор (4) обеспечит равномерное приближение на всё отрезке [0, π].

Таким образом, в ходе работы над статьей были исследованы аппроксимативные свойства sinc-приближений, погрешность в точке классических sinc-аппроксимаций, приближена произвольная функция классическим и модифицированным оператором.