Линейные цепи при периодическом негармоническом воздействии

В современном мире системы передачи информации формируются из различных по характеру блоков. Большую их часть можно отнести к линейным цепям, либо к нелинейным. При испытании систем передачи информации и снятии их характеристик используют специальные тестовые сигналы, которые могут быть и периодическими [1]. Часто при исследовании процессов в линейных цепях приходится сталкиваться с трудоемкими аналитическими преобразованиями, и при этом конкретные примеры требуют численных расчетов. Поэтому в таких случаях можно обратиться к компьютерному программированию, а конкретно, к математической системе Mathcad. Она позволяет проводить преобразования как в аналитической форме, так и численно, и полученные результаты легко представить в виде графиков.

В данной работе была поставлена задача написания в Mathcad программы, которая позволяла бы исследовать преобразование периодического сигнала в линейной цепи, и проверки ее работоспособности.

В первой части программы производятся анализ спектра периодического сигнала и восстановление его временной функции по полученным параметрам спектра, что позволяет оценить правильность найденных параметров спектра и определить активную ширину спектра сигнала.

Во второй части программы производится анализ линейной активной цепи методом узловых потенциалов и определяются ее частотные характеристики.

В третьей части программы определяются спектр и временная функция отклика линейной активной цепи на периодическое воздействие.

Работоспособность программы и правильность получаемых результатов были проверены на ряде примеров. На рис. 1 приведены временная функция и амплитудный спектр периодического воздействия. На рис. 2 представлены амплитудно-частотная и фазово-частотная характеристики линейной активной цепи второго порядка. Точки на этих графиках соответствуют частотам гармоник в спектре воздействия. На рис. 3 представлены временная функция отклика и амплитудный спектр отклика линейной активной цепи с характеристиками рис.1 на периодическое воздействие с характеристиками рис. 2.

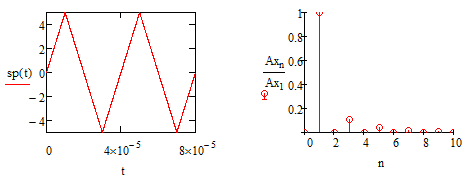
Рисунок 1. Временная функция и амплитудный спектр периодического воздействия

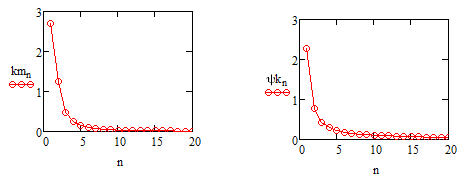
Рисунок 2. Амплитудно-частотная и фазово-частотная характеристики цепи

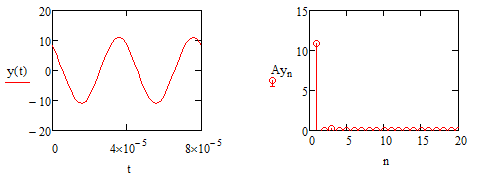
Рисунок 3. Временная функция отклика и амплитудный спектр отклика цепи

Исследованная в этом примере цепь по типу является фильтром нижних частот. Поэтому изменения формы сигнала, которые можно обнаружить, сравнивая рис. 1 и рис. 3, вполне объяснимы. Сглаживание верхушек треугольных импульсов является следствием подавлением линейной цепью верхних частот в спектре воздействия [2].

 В ходе нашего исследования в цепи были проведены некоторые изменения, а конкретно, уменьшены емкости конденсаторов исследуемой цепи в 2 и в 4 раза. На рис. 4 представлены временная функция отклика линейной цепи с емкостями конденсаторов в 2 раза меньше начальных. На рис. 5 соответственно для емкостей конденсаторов в 4 раз меньше начальных.  

Рисунок 4. Временная функция отклика линейной цепи с емкостями конденсаторов в 2 раза меньше начальных

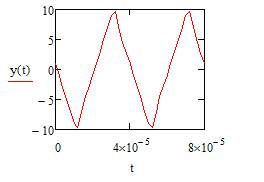
Рисунок 5. Временная функция отклика линейной цепи с емкостями конденсаторов в 4 раза меньше начальных

Если еще раз сравнить рис. 1, но уже с рис. 4 и рис. 5, можно так же заметить изменение формы сигналов. Сигнал на выходе линейной цепи становится все более похожим на входной сигнал, так как ослабляется подавление верхних частот в спектре воздействия.