Алгоритмы для анализа ответов открытых вопросов тестирования
Секция: Технические науки

XVII Студенческая международная научно-практическая конференция «Технические и математические науки. Студенческий научный форум»
Алгоритмы для анализа ответов открытых вопросов тестирования
Algorithms for analyzing answers to open test questions
Madiyar Seiitzhanov
master student, International University Information Technology, The Republic of Kazakhstan, Almaty
Vasiliy Serbin
candidate of Science, associate Professor, International University Information Technology, The Republic of Kazakhstan, Almaty
Аннотация. На сегодняшний день очень популярны использовать тесты, чтобы определить уровень знания человека. В тесте встречаются закрытые и открытые вопросы. Открытый вопрос дает более подробную и разнообразную информацию. В этом случае открытый вопрос – неотъемлемый компонент опросника.
В этой статье рассматриваются алгоритмы для анализа ответов открытых вопросов. Подробно описываются и проводится сравнительный анализ таких алгоритмов как, расстояние Хемминга, расстояние Левенштейна, сходство Джаро - Винклера.
Abstract. Today it is very popular to use tests to determine the level of knowledge of a person. In the test, there are closed and open questions. An open question provides more detailed and diverse information. In this case, an open question is an integral component of the questionnaire.
This article discusses the algorithms for analyzing the answers to open-ended questions. The comparative analysis of such algorithms as the Hamming distance, the Levenshtein distance, the Jaro – Winkler similarity are described and carried out in detail.
Ключевые слова: тестирования; алгоритмы; e-learning; сравнение алгоритмов тестирования; анализ тестирования.
Keywords: testing; algorithms; e-learning; comparison of testing algorithms; test analysis.
1.Введение
Результаты тестирования – это очень важный момент в процессе обучения. Они представляют собой не просто итоговый балл учащихся за тот или иной тест, а позволяют подробно проанализировать процессы выполнения теста одним учащимся или сразу группой учащихся. Тест может содержаться из разных типов вопросов. Вопросы с одним или нескольким ответом или открытые вопросы. Подробный анализ результатов тестирования позволяет преподавателю увидеть основные типичные ошибки учащихся и еще раз обратить на них внимание. Для анализа ответов открытых вопросов можно использовать разные алгоритмы. Основываясь на свойствах операций, алгоритмы подобия строк можно классифицировать на несколько типов [1, с.7]:
1. На основе расстояния
2. На основе токенов
3. На основе последовательности
2.Виды алгоритмов
На основе расстояния: алгоритмы, попадающие в эту категорию, пытаются вычислить количество операций, необходимых для преобразования одной строки в другую. Чем больше количество операций, тем меньше сходство между двумя строками. Следует отметить, что в этом случае каждому символу индекса строки придается одинаковое значение.
На основе токенов: в этой категории ожидаемый ввод - это набор токенов, а не полные строки. Идея состоит в том, чтобы найти похожие токены в обоих наборах. Чем больше общих токенов, тем больше сходство между наборами. Строка может быть преобразована в наборы путем разделения с помощью разделителя. Таким образом, мы можем преобразовать предложение в токены слов или n-граммовых символов. Обратите внимание, что здесь токены разной длины имеют одинаковое значение.
На основе последовательности: Здесь сходство является фактором общих подстрок между двумя строками. Алгоритмы пытаются найти самую длинную последовательность, которая присутствует в обеих строках, чем больше этих последовательностей найдено, тем выше оценка сходства. Обратите внимание, что здесь комбинация символов одинаковой длины имеет одинаковое значение.
2.1 Расстояние Хемминга
Расстояние вычисляется путем наложения одной строки на другую и нахождения мест, где строки изменяются [2, с.7]. Обратите внимание, что классическая реализация предназначена для обработки строк одинаковой длины. Некоторые реализации могут обойти это, добавляя дополнение в префиксе или суффиксе. Тем не менее, логика состоит в том, чтобы найти общее количество мест, где одна строка отличается от другой.
Даны строки s1 “karolin” и s2 “katerin”. Представим их пересечение в табличном виде:
Таблица 1.
Расстояние Хемминга
|
k |
a |
r |
o |
l |
i |
n |
|
k |
a |
t |
h |
r |
i |
n |
|
0 |
0 |
1 |
1 |
1 |
0 |
0 |
Как видим из таблицы s1 и s2 отличаются на 3 буквы. Чтобы рассчитать коэффициент сходство:
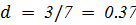
2.2 Расстояние Левенштейна
Расстояние вычисляется путем нахождения количества правок, которые преобразуют одну строку в другую. Допустимые преобразования: вставка - добавление нового символа, удаление - удаление символа и подстановка - замена одного символа другим. Выполняя эти три операции, алгоритм пытается изменить первую строку, чтобы она соответствовала второй. В конце мы получаем расстояние редактирования. [3, с.7].
Даны строки s1 “saturday” и s2 “sunday”. Представим их пересечение в табличном виде:
Таблица 2.
Расстояние Левенштейна
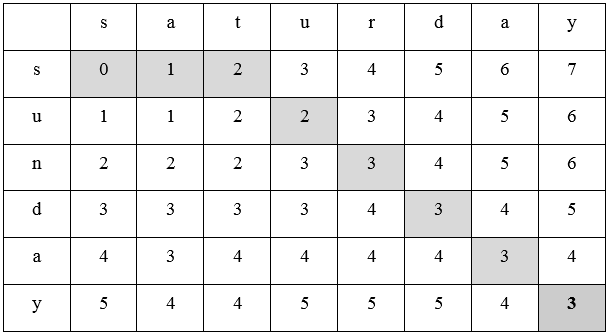
Чтобы преобразовать s1 в s2 нам потребуется сделать следующие операции:
● Удалить букву a
● Удалить букву r
● Заменить букву r на n
В итоге получается 3 операции. Чтобы рассчитать коэффициент cходство:
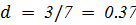
2.3 Сходство Джаро - Винклера
В области информатики и статистики сходство Джаро - Винклера представляет собой меру схожести строк для измерения расстояния между двумя последовательностями символов. Это вариант, который в 1999 году предложил Уильям Э. Винклер на основе расстояния Джаро [4, с.7]. Этот алгоритм дает высокие оценки двум строкам, если они содержат одинаковые символы, но на определенном расстоянии друг от друга, и порядок совпадающих символов одинаков. Точнее, расстояние нахождения подобного символа на 1 меньше половины длины самой длинной строки. Таким образом, если длина самой длинной строки равна 5, символ в начале строки 1 должен быть найден до или на ((5/2) –1) ~ 2-й позиции в строке 2, чтобы считаться действительным соответствием. Из-за этого алгоритм является направленным и дает высокую оценку, если сопоставление выполняется с начала строк.
Даны строки s1 martha и s2 marhta. Представим их пересечение в табличном виде:
Таблица 3.
Сходство Джаро - Винклера
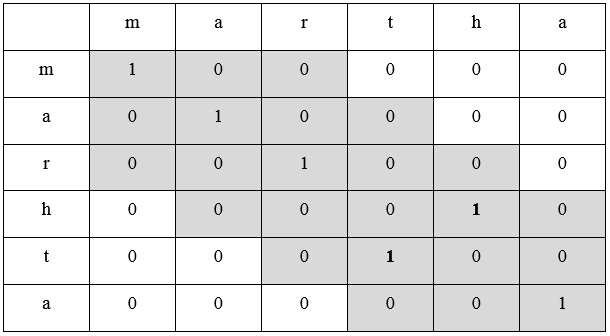
Здесь максимальное расстояние составляет 6/2 — 1 = 2. В выделенных ячейках приведенной таблицы указаны единицы, когда символы идентичны (имеется совпадение), и нули в противном случае.
Получается:
● m = 6
● s1 = 6
● s2 = 6
● Есть несовпадающие символы T/H и Н/Т, в результате: t = 2/2 = 1
Расстояние Джаро:
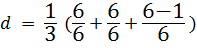 = 0.94
= 0.94
Чтобы найти результат Джаро — Винклера с помощью стандартного веса
p = 0.1 мы продолжаем искать:
l = 3
Таким образом:
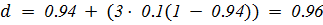
Коэффициент сходства s1 и s2 равна 0.9
3. Сравнения алгоритмов
На основе проведенного обзора, проведен сравнительный анализ (Таблица 4).
Таблица 4.
Сравнения алгоритмов
|
Строка 1 |
Строка 2 |
Расстояние Хемминга |
Расстояние Левенштейна |
Сходство Джаро - Винклера |
|
текст |
тест |
0.0 |
0.8 |
0.63 |
|
алгоритм |
алгоиртм |
0.75 |
0.75 |
0.86 |
|
разработка |
разработчик |
0.0 |
0.72 |
0.90 |
|
компьютер |
терпьюком |
0.3 |
0.3 |
0.55 |
|
документ |
доктор |
0.0 |
0.3 |
0.62 |
|
книга |
карта |
0.4 |
0.4 |
0.6 |
|
друзья |
дорога |
0.16 |
0.16 |
0.4 |
|
кровать |
ватт |
0.0 |
0.42 |
0.0 |
5. Заключения
Выбор алгоритма подобия строк зависит от варианта использования. Все вышеперечисленные алгоритмы, так или иначе, пытаются найти общие и не общие части строк и разложить их на части, чтобы получить оценку сходства. И без усложнения процедуры большинство вариантов использования может быть решено с помощью одного из этих алгоритмов.





