История возникновения теории графов и ее приложения в различных областях науки и техники

Теория графов — это  раздел дискретной математики, который изучает свойства графов. Говоря простым языком, граф представляет из себя множество вершин (узлов), соединённых рёбрами. Чтобы получить какое то поверхностное представление о графе можно рассмотреть несколько примеров. Схема метро или любой какой либо другой маршрут является типичным графом. Программистам знакома компьютерная сеть , которая тоже является графом. Например, точки в компьютерной сети – это отдельные серверы ,а линиями можно назвать различные виды электрических сигналов. На первом месте в метрополитене находятся станции, на втором туннели, которые проложены между ними. То есть мы  можем сказать, что граф – это совокупность вершин, соединенных ребрами.

Первые задачи из раздела теории графов в основном были связаны с решением математических развлекательных задач и головоломок. Родоначальником теории графов принято считать Леонарда Эйлера .В 1736 году в одном из своих писем он сформулировал и предложил решение задачи о семи кёнигсбергских мостах, ставшая впоследствии одной из классических задач теории графов.

Задача о Кёнигсбергских мостах. На рисунке 1 мы можем наблюдать схематический план центрального района города Кёнигсберг, который включает в себя два берега реки, два острова в ней и семь соединяющих мостов. А смысл этой задачи таков, требуется обойти все четыре части суши, пройдя при этом по каждому мосту всего один раз, и вернутся в исходную. Что бы доказать, что у задачи нет решения, Эйлер обозначил каждую часть суши - точкой (вершиной), а каждый мост - линией (ребром),которая соединяет соответствующие им точки. Мы получили «граф» (рисунок 2). Эйлер смог обобщить постановку задачи и найти критерии существования обхода (назовем его специальным маршрутом) у этого графа, а именно граф должен быть связным и каждая его вершина будет принадлежать четному числу ребер.

Рисунок 1. Схематический план центрального района города Кёнигсберг

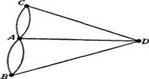
Рисунок 2. Граф

Правило Эйлера:

1. В графе, который не имеет  вершин нечетных степеней существует обход всех рёбер (причем каждое ребро проходится один раз) с началом в любой вершине графа.

2. В графе, имеющем только две вершины с нечетными степенями, существует обход с началом в одной вершине с нечетной степенью и концом в другой.

3. В графе, имеющем более двух вершин с нечетной степенью, такого обхода не существует.

1. Задача про три дома и три колодца. У нас есть три дома и три колодца, которые  расположены на плоскости в  произвольным порядке. И мы должны от каждого дома к каждому колодцу провести тропинку ,да так, чтобы тропинки не пересекались (рисунок 2).Эту задачу решил Куратовский  в 1930 году. Он смог показать, что решения не существует

Рисунок 2.

3. Задача о четырех красках. Смысл задачи заключается в раскрашивании карты таким образом, чтобы ни одна соседняя область не была закрашена одним цветом  (рисунок 3) . С конца позапрошлого века мы знаем гипотезу, что для этого было достаточно четырех красок. В опубликованном в 1976 году решении Аппеля и Хейкена задачи о четырех красках оно базировалось на переборе множества вариантов с помощью компьютера. Решение этой задачи «программным путем» стало прецедентом ,что в свою очередь породило не законченную по сегодняшний день бурную дискуссию. Смысл  данного  решения состоит в том, чтобы перебрать большое, но конечное число (приблизительно 2000) типов потенциальных контрпримеров к теореме о четырех красках и показать, что ни один случай не является контрпримером. Данный перебор производился программой суперкомпьютера около тысячи часов.

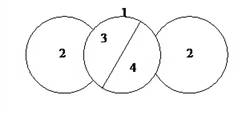
Рисунок 3.

ТЕОРИЯ ГРАФОВ В РАЗЛИЧНЫХ  ОБЛАСТЯХ НАУКИ И ТЕХНИКИ

Мы можем встретиться с графами почти везде. Графы являются замечательными математическими объектами, благодаря которым можно решать и упрощать множество задач. Некоторые математические факты удобнее будет формулировать с помощью графов, и невозможно не заметить её принадлежность ко многим наукам. Иногда мы рисуем на листе бумаги кружочки, квадратики, точки обозначая ими людей, населённые пункты, дела, которые нам нужно сделать и прочее, и соединяем их прямыми и ломаными линями, стрелочками обозначающими связи между ними, отношения, последовательность действий. Примеры применения теории графов легко можно наблюдать в таких областях, как физика, химия, теория связи, проектирование вычислительных машин, электротехника, машиностроение, архитектура, исследование операций, кибернетика, общая теория систем, общая теория организаций, генетика, психология, было социология, экономика, антропология, лингвистика и другие науки.

Электрические цепи. В 1847 году Киргофом была разработана теория деревьев, с помощью  которой можно  найти показатель силы тока в каждом проводнике (дуге) и в каждом контуре, который  рассматривается в данной электрической цепи. Будучи физиком по образованию, он подходил к решению задач как математик. Что же сделал Кирхгоф? Он поменял каждую электрическую цепь на соответствующий ей граф и показал, что для того чтобы  решить систему уравнений нет необходимости рассматривать каждый цикл графа электрической цепи  по отдельности.

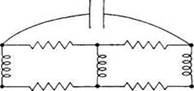
Рисунок 3.Сеть N и соответствующий ей граф G

В социальной психологии. В 1936 году психологом Куртом Левиным было высказано предположение о том, что «жизненное пространство» индивидуума представляется с  помощью планарной карты. На этой карте области обозначают различные типы человеческой деятельности, то есть все то , что он делает на работе, дома, или же его хобби. Данная точка зрения позволила прийти психологам к другой психологической интерпретации графа, в которой людей можно обозначить вершинами, а их отношения - ребрами. Этими отношениями будут, например, любовь, ненависть, общение, подчинение. То что предположил Левин, может относится только к планарным картам, так как он всегда рисовал свои рисунки на плоскости. В конечном итоге идея К. Левина была развита в четыре социометрических процедурах. Таким образом, специальной общей теории, которая может быть применима в любой сфере жизнедеятельности человека была обусловлена потребностями практики. Это и есть «Теория графов».

Графы и информация. Двоичные деревья являются важной в теории информации. Мы можем предположить, что какое то число сообщений нужно закодировать в виде конечных последовательностей различной длины, которая  состоит  из нулей и единиц. Если вероятности кодовых слов нам заданы, то самым лучшим будет считаться код, у которого  общая средняя длина слов будет минимальна по сравнению с прочими распределениями вероятности. Задачу о построении такого оптимального кода можно решить алгоритм Хаффмана. Двоичные кодовые деревья допускают интерпретацию в рамках теории поиска. Каждой вершине при этом может быть сопоставлен вопрос, ответить на который можно " да", или " нет". Положительному и негативному ответу будут соответствовать два ребра, которые  выходят из вершины. "Опрос" заканчивается, когда удалось  установить то, что требовалось. Так что, если кому-то нужно будет взять интервью у различных людей, и ответ на следующий вопрос будет зависеть от заранее неизвестного нам ответа на предыдущий вопрос, то план этого интервью может быть  представлен в виде двоичного дерева.

Графы и химия.

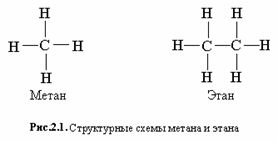
Молекулу каждого предельного углеводорода можно рассмотреть как дерево. Если мы удалим все атомы водорода, то оставшиеся атомы углеводорода также будут образовывать дерево, каждая вершина которого имеет степень не выше 4. Отсюда следует ,что число возможных структур предельных углеводородов, этого вещества, будет равно числу деревьев с вершинами степени не больше четырех. Как видим, подсчет числа гомологов предельных углеводородов тоже приводит к задаче о перечислении деревьев некоторого типа. Эту задачу и ее обобщения рассмотрел Д.Пойа.

Графы и биология. Деревья играют немаловажную роль в биологической теории ветвящихся процессов. Вполне достаточно будет рассмотреть только одну разновидность ветвящегося процесса – размножение бактерий. Можно предположить, что через какой то промежуток времени каждая бактерия делится на две новые, или погибает. И тут для потомства одной бактерии мы получаем двоичное дерево.

Графы и физика. Еще совсем недавно одной из наиболее сложных и утомительных задач для радиолюбителей являлось конструирование печатных схем. Печатная схема-  это пластинка из какого-либо диэлектрика, на которой в виде металлических полосок вытравлены дорожки. Пересекаются  дорожки только в определенных точках, где устанавливаются необходимые элементы такие как иоды, триоды, резисторы , их пересечение в других местах может вызвать замыкание всей электрической цепи. В процессе решения данной задачи нужно удалить плоский граф, с вершинами в этих точках. И так же стоит не забывать, что графы нам встретятся и на карте звездного неба.

Графы и математика. Самый очевидный и яркий примером можно выразить многогранники. Например, вершины и ребра куба рассматриваются как вершины и ребра графа. Так же графы под другими названиями будут встречаться нам в учебниках химии, биологии и географии, где они используются для наглядного и упрощенного описания различных схем организаций, логических возможностей, классификаций, только в том случае  когда соответствующие круги пересекаются. Все вышесказанное может смело доказать тот факт что с помощью теории  графов можно создавать точные математические модели реальных  объектов и ситуаций, с которыми достаточно легко и несложно оперировать. Необходимо отметить, что условия приведенных в статье задач, не являются сухими математическими формулировками, а напротив, являются жизненными ситуациями, что в свою очередь отражает актуальность и немаловажность затронутой нами темы. Также можно сделать несколько выводов:

А) Теория графов используется  как любопытный инструмент, нужный  для решения различных задач-головоломок;

Б) С помощью теории графом мы можем быстро и изящно решить задачу, которую будет трудно решить любым другим методом;

В) Теория графов находит многочисленные применения в различных практических вопросах;

Г) Используя методы решения задач с помощью теории графов можно решить не только одну конкретную задачу, а становится возможным решение целого класса задач (данное свойство графов используется в программировании, где существует целый класс алгоритмов).

Подводя итог ,можно отметить практическую ценность теории графов, доказательство которой было целью этой статьи.