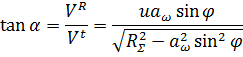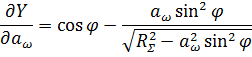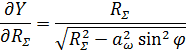Методика проведения геометрического расчета волновой передачи с промежуточными телами качения
Секция: Технические науки

XXXIV Студенческая международная научно-практическая конференция «Технические и математические науки. Студенческий научный форум»
Методика проведения геометрического расчета волновой передачи с промежуточными телами качения
В последнее время активно исследуются и развиваются механизмы преобразования движения, в которых используется не зубчатое зацепление, а новый тип зацепления с помощью периодических дорожек качения и промежуточных тел качения, которые находятся в постоянном контакте с соответствующими поверхностями зацепляющихся звеньев, что позволяет реализовать многопарное зацепление. Это механизмы, в которых ролики или шарики не просто заменяют зубья зубчатого колеса, а, имея несколько степеней свободы, образуют механизмы принципиально новой конструкции, обладающие новыми функциями и параметрами. Теория зацепления данных передач долгое время имела прикладное значение в ракетно-космических и оборонных проектах. На сегодняшний день области применения таких передач - силовые передаточные механизмы, редукторов, приводов, мультипликаторов широкого назначения. Такие механизмы рассматривают как волновые передачи с промежуточными телами качения, в которых роль гибкого колеса играют тела качения и каждое из тел качения совершает волнообразное перемещение относительно жесткого колеса.
Технические особенности и преимущества волновой передачи с промежуточными телами качения:
- Высокое передаточное число.
- Высокие крутящие моменты на выходном звене.
- Компактность.
- Высокий КПД, составляющий 0,8-0,9, а в специальной конструкции - до 0,97.
- Малый момент инерции, высокий уровень динамичности.
- Малый угловой зазор.
- Малая вибрация.
- Высокая надежность и продолжительный срок службы.
Волновые передачи с промежуточными телами качения (ВППТК) являются гибридом двух видов передач - механических передач с промежуточными телами качения и волновыми зубчатыми передачами. Заимствовав лучшие качества обеих передач, ВППТК позволяет получить и новые преимущества, например снижение нижнего предела передаточного числа по сравнению с волновыми зубчатыми пеедачами. Использование в данных передачах тел качения, которые выпускаются шарикоподшипниковой промышленностью, с высокой точностью геометрических размеров, требуемой шероховатостью рабочих поверхностей, термообработки, высококачественных марок сталей и др., что при соответствующем изготовлении жёсткого колеса и генератора обеспечивает длительный срок работы передач с сохранением их функциональности.
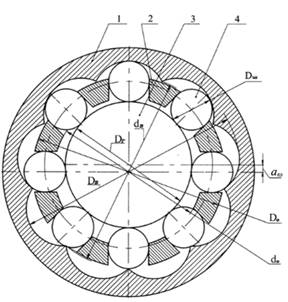
Рисунок 1. Волновая передача с промежуточными телами качения
Основой рассматриваемых передач является конструкция, представленная на рисунке 1. Генератор волн, эксцентрик 1, вращаясь, вызывает радиальные перемещения шариков 4 в пазах обоймы 3. Шарики 4 контактируют с поверхностями зубьев жёсткого колеса 2. Разность числа шариков и зубьев жёсткого колеса, обычно при эксцентриковом генераторе равная единице, обеспечивает редукцию движения выходного звена передачи. Выходным звеном могут служить обойма с шариками или жёсткое колесо, при фиксации одного из них относительно корпуса.
Конструкции передач с адаптивными генераторами, обеспечивающие зацепление без зазоров, позволяют повысить их качество прежде всего за счёт точности и долговечности.
Геометрические соотношения в данной передаче описываются с использованием заменяющего аксиального кривошипно-шатунного механизма (рисунок 2). Ведущим кривошипом является эксцентрик генератора. Длина ведущего эксцентрика равна величине эксцентриситета ![]() . Значение
. Значение ![]() рекомендуется принимать равным 0,25
рекомендуется принимать равным 0,25![]() [1], что приемлемо для данных передач. Линию, соединяющую центры шариков
[1], что приемлемо для данных передач. Линию, соединяющую центры шариков ![]() и эксцентрика
и эксцентрика  , заменяет шатун. Назовём длину этой линии приведённым радиусом генератора
, заменяет шатун. Назовём длину этой линии приведённым радиусом генератора ![]() . Видно, что линия проходит через точку контакта шарика с генератором. Тогда
. Видно, что линия проходит через точку контакта шарика с генератором. Тогда 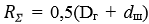 , где
, где  ,
, 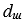 - диаметры генератора и шарика [2]. Для геометрического расчета будем использовать систему компьютерной алгебры из класса систем автоматизированного проектирования - Mathcad.
- диаметры генератора и шарика [2]. Для геометрического расчета будем использовать систему компьютерной алгебры из класса систем автоматизированного проектирования - Mathcad.
Диаметр генератора и тел качения  =52мм,
=52мм, 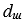 =5мм, соответственно. Исходя из этого, приведенный радиус генератора
=5мм, соответственно. Исходя из этого, приведенный радиус генератора ![]() равен 28,5 мм, а величина эксцентриситета равна 1,25 мм.
равен 28,5 мм, а величина эксцентриситета равна 1,25 мм.
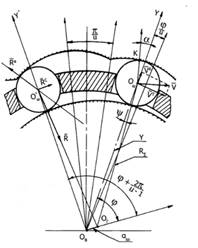
Рисунок 2. Схема кривошипно-шатунного механизма
Пазы обоймы, которые являются направляющими для шариков, выполнены радиальными. Поэтому считаем, что центры шариков движутся по оси пазов. Обозначив Y расстояние от центра шарика ![]() до центра зубчатого венца жёсткого колеса Ок, (рисунок 7), получаем выражение:
до центра зубчатого венца жёсткого колеса Ок, (рисунок 7), получаем выражение:
|
|
(1) |
где φ - текущий угол поворота входного звена.
Вычислив данное выражение, получаем значения расстояния от центра шарика до центра зубчатого венца (рисунок 3).

Рисунок 3. полученные значения расстояния от центра шарика до центра зубчатого венца
Выражение (1) определяет положение центра шарика. Для получения уравнений профиля зубьев жёсткого колеса, перейдём в систему координат, жёстко связанную с вращающимся венцом. Зубчатый венец жёсткого колеса вращается в и раз медленнее генератора, где u - число зубьев зубчатого венца и передаточное число передачи (если Z - число шариков, то u = Z +1), и переход осуществляется поворотом системы координат на угол φ/u. В новой системе координат центр шарика ![]() опишет траекторию, описываемую центром шарика. Профиль зуба опишет точка К на шарике. Отрезок
опишет траекторию, описываемую центром шарика. Профиль зуба опишет точка К на шарике. Отрезок ![]() К перпендикулярен касательной к профилю зуба, и угол а является углом передачи движения профилю. Чтобы его определить, допустим, что скорость движения центра шарика V относительно венца имеет две составляющие: радиальную
К перпендикулярен касательной к профилю зуба, и угол а является углом передачи движения профилю. Чтобы его определить, допустим, что скорость движения центра шарика V относительно венца имеет две составляющие: радиальную ![]() , определить которую можно, продифференцировав (1) по φ с учётом того, что её производная по времени есть постоянная угловая скорость ω вращения входного звена:
, определить которую можно, продифференцировав (1) по φ с учётом того, что её производная по времени есть постоянная угловая скорость ω вращения входного звена:
|
|
(2) |
и тангенциальную ![]() , возникающую из-за вращения венца жёсткого колеса и равную
, возникающую из-за вращения венца жёсткого колеса и равную ![]() . Поскольку скорость шарика направлена по касательной к профилю, то α определится следующим выражением:
. Поскольку скорость шарика направлена по касательной к профилю, то α определится следующим выражением:
|
|
(3) |
На рисунке 4 представлены результаты вычислений выражений (2) и (3).

Рисунок 4. Полученные значения радиальной и тангенциальной составляющих, и угла α
Параметрические уравнения профиля зуба с учётом выражений (1) и (3) будут следующие:
|
|
(4) |
|
|
(5) |
Решив данные параметрические уравнения, получаем координаты точек профиля зубчатого венца, представленные на рисунке 5.
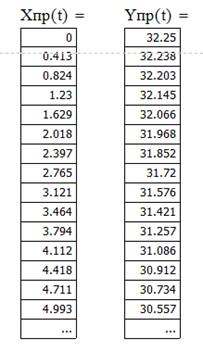
Рисунок 5. Координаты точек зубчатого венца
Для проверки правильности решения, построим, по полученным координатам, график (рисунок 6).
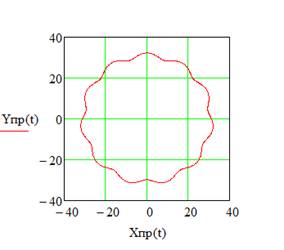
Рисунок 6. Профиль зубчатого венца
Важным кинематическим параметром передачи является коэффициент перекрытия, определяемый длиной рабочего участка линии зацепления. Зацепление шарика с профилем заканчивается в точке пересечения его с соседним профилем. Координаты точки пересечения двух соседних профилей определяются из трансцендентного уравнения [3].
|
|
(6) |
Решив данное уравнение в среде MathCad, получаем следующие координаты точек пересечения профилей (рисунок 7).
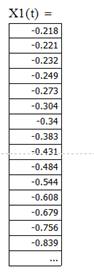
Рисунок 7. Координаты точек пересечения профилей
Угол ![]() , который соответствует концу линии зацепления, определяется из уравнении (4)-(6). Для этого угол φ заменяем углом
, который соответствует концу линии зацепления, определяется из уравнении (4)-(6). Для этого угол φ заменяем углом![]() . Начало зацепления определяется из известного условия: движение не передается, если угол передачи движения меньше угла трения [4]. Угол соответствующий началу
. Начало зацепления определяется из известного условия: движение не передается, если угол передачи движения меньше угла трения [4]. Угол соответствующий началу ![]() зацепления, находится из соотношения (1), при замене
зацепления, находится из соотношения (1), при замене ![]() углом φ, с учётом коэффициента трения:
углом φ, с учётом коэффициента трения:
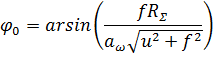
где f- приведенный коэффициент трения.
![]()
Для зубчатого венца жёсткого колеса диаметр выступов ![]() определится из уравнений (4) и (5), при φ=
определится из уравнений (4) и (5), при φ=![]() . Диаметр окружности впадин находим из простого соотношения:
. Диаметр окружности впадин находим из простого соотношения:
![]() .
.
![]()
Диаметры обоймы - наружный ![]() и внутренний выбираются из условия, чтобы наружный диаметр обоймы был меньше диаметра выступов зубчатого венца жёсткого колеса, а наружный диаметр эксцентрика не касался внутреннего диаметра обоймы:
и внутренний выбираются из условия, чтобы наружный диаметр обоймы был меньше диаметра выступов зубчатого венца жёсткого колеса, а наружный диаметр эксцентрика не касался внутреннего диаметра обоймы:
![]() .
.
Рассмотрим изменения в работе передачи, обусловленные отклонениями параметров от идеально точных. При реальном проектировании механизма необходимо знать круг параметров, значения которых могут отклоняться от заданных, диапазоны этих отклонений, возможность управлять ими, а также определить чувствительность выходной функции к отклонениям входящих в неё параметров. В линейной постановке задача определения чувствительности обобщенной выходной функции ![]() решается с помощью зависимости:
решается с помощью зависимости:
![]() ,
,
где ![]() - значения параметров; Δ
- значения параметров; Δ![]() - отклонения параметров.
- отклонения параметров.
Выходной функцией передачи является функция Y, определяемая из формулы (1). Чувствительность Y к отклонениям ![]() и
и ![]() выражается частными производными по следующим параметрам:
выражается частными производными по следующим параметрам:
|
|
(7) |
|
|
(8) |