Применение теории вероятности на практике

Сталкиваясь в жизни с различными ситуациями, когда всё решает случай, невольно задумываешься: как какое-либо действие может повлиять на исход? С какой вероятностью произойдёт то или иное событие? На данные вопросы может ответить теория вероятности. Она выявляет закономерности случайных явлений, изучает случайные события, случайные величины. Свойства и операции, которые производятся над ними. По сути, это изучение степени возможности возникновения какого-то события.

В истории известен случай, когда один испанец выиграл в национальную лотерею. Причём номер его билета оканчивался числом 48. Когда мужчина давал интервью и рассказывал, почему он выбрал именно этот билет с конкретно такими цифрами, его слова немного удивили многих, кто мог слышать или читать данное интервью. Мужчина сказал, что последнюю неделю ему снилась исключительно цифра 7, и, соответственно, перемножил количество дней в неделе на то самое заветное число, которое он видел во сне. Но возникает вопрос: «Почему 48?», ведь знающий таблицу умножения человек скажет, что ответ будет 49 и будет прав. Да, испанец ошибся, но этот просчёт позволил ему выиграть деньги, поэтому ошибка сразу же трансформируется в удачу. Так вот в этом случае как раз и появляется интерес к столь загадочной науке, как теория вероятности. Эта научная дисциплина изучает то, как в условиях недостаточной и неточной информации человек способен формировать суждения и принимать более правильные решения, не основываясь лишь на одной только интуиции.

На мой взгляд, необходимо рассмотреть фундаментальный инструмент, использующийся в теории вероятности. Таковым является комбинаторика - раздел, который  изучает дискретные объекты, множества (сочетания, перестановки, размещения и перечисления элементов) и отношения на них (например, частичного порядка). Комбинаторика является важным инструментом для подступа к вероятности.

Возьмём для примера игру под названием «Покер». На практике стало понятно, что одно лишь знание комбинаций и правил не даст вам желаемого результата или хотя бы стабильного выигрыша в этой карточной игре. Зачастую огромное значение имеет умение быстро анализировать ситуацию за столом, просчитывать и вычислять, какие комбинации могут быть у ваших соперников, учитывая то, какие карты лежат на столе. Именно комбинаторика и отвечает за этот аспект игры. Благодаря ей, вы можете подсчитать свои шансы на формирование сильной руки.

Для хорошей игры необходимо усвоить некоторые основные правила. Во-первых, нужно знать, что такое ауты. Ауты - это те карты в колоде, которые могут дать вам более выгодную, то есть выигрышную позицию (руку). Во-вторых, флоп - это первый этап, при котором на стол выкладываются три карты из общей колоды. Именно флоп в покере является тем периодом, когда необходимо собрать максимум информации о сложившейся ситуации. Затем, когда открывается по одной карты из колоды, два этапа, идущих друг за другом называются «тёрн» и «ривер».

Чтобы понять суть использования теории вероятности в покере, рассмотрим нюансы на практике.

Пусть у игрока на руках Дама и Король, на игровом столе лежат Король, 4 и 10. В данном примере масть карт не так важна, поэтому мы её не будем учитывать. Попробуем вычислить, каковы у оппонентов шансы на пару Десяток, а также дополнение в виде связки Туз-Король.

Если речь идет о непарных руках (в случае с нашим примером это Туз и Король), то используется такая формула: А1*А2. В данной формуле А1 представляет собой общее число карт в колоде в отношении первой карты (Туз). Следовательно, А2 – тоже самое только в отношении второй карты (Король).

Умножая данные о двух доступных картах, мы получаем то совокупное число свободных комбинаций. В данной ситуации станет понятно, что либо на руках, либо в колоде присутствуют еще 2 Короля и 4 Туза. Нам необходимо умножить 2 на 4 и мы получим 8. Именно такое число разнообразных комбинаций Туз-Король, которые потенциально могут угрожать нам.

Теперь нужно изучить число возможных вариантов, которые связаны с парой карманных десяток. Ведь если у кого-то будет карманная пара Десяток, то в совокупности с той 10, которая лежит на общем столе, может быть сформирована комбинация Тройка. Для этого нам нужно будет использовать другую формулу.

Речь идет о формуле А*(А-1)/2. В данном случае, А будет представлять собой число карт этого номинала, которые остаются в колоде либо на руках у кого-то из оппонентов. Также мы видим на игровом столе одну Девятку, что говорит о том, что в игре еще может быть 3 таких карты. Тем самым, формула приобретает такой вид – 3*(3-1)/2 =3. Именно таким будет число комбинаций из парных Десяток.

Сделав данные вычисления можно сказать, что не так уж и сложно, как это может показаться, просчитать возможные варианты в игре, и одновременно приблизительно понять и проанализировать, какие у нас шансы на успех в данной раздаче.

Для этого нужно лишь сделать не самые тяжелые математические расчёты. К тому же многие играют в покер онлайн, а ведь при таком способе можно использовать различные программы, которые направлены на подсчёт вероятности возможного выигрыша с учётом того, какие карты у вас уже на руках. Но, если вы всё же предпочитаете играть в покер за реальным столом, то тогда придётся делать расчёты в уме.

Рассмотрим ещё одну несложную игру, в которой используется теория вероятности.

Предположим, что дежурный в классе выбирается из двух человек с помощью «считалочки». Считать необходимо до того числа, которое является суммой чисел так называемых «выброшенных» пальцев одной руки каждого участника игры. Тот счастливчик, на котором счёт остановился, не является дежурным, а, соответственно, оставшийся и будет дежурить.

Каким же образом можно оценить шансы участников в этой игре?

Стоит заметить, что, если сумма «выброшенных» пальцев окажется нечетной, то участник, с кого начинается счёт,  не будет дежурным, а если четной, то наоборот - второй участник

Для наглядности необходимо составить вероятностное дерево:

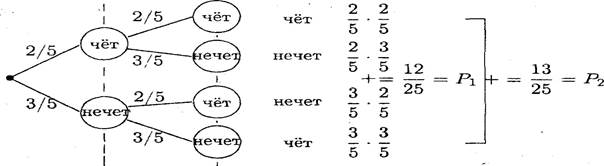
Р1 — вероятность дежурства первого участника, а Р2 вероятность дежурства второго участника. С учетом того, что P1 = 13/25 > Р2 = 12/25, участнику игры можно рекомендовать в этом случае стоять вторым.

Рисунок 1. Вероятностное дерево

Итак, исходя из всего вышеизложенного, можно сказать, что теория вероятности исследует вероятностные закономерности случайных явлений. Различные методы, которые были выявлены в теории вероятности, применяются в различных современных науках, а также в повседневной деятельности человека. Например, в играх. В некоторых случаях именно благодаря пониманию методологии работы теории вероятности можно достичь успеха в той или иной игре.