Колебания в электроэнергетике и их математические модели
Секция: Технические науки

XXXIX Студенческая международная научно-практическая конференция «Технические и математические науки. Студенческий научный форум»
Колебания в электроэнергетике и их математические модели
Низкочастотные колебания мощности являются одной из основных проблем надежности и функционирования энергосистем во всем мире. Это связано с тем, что наличие таких колебаний может значительно снизить допустимые перетоки мощности в системе и, как следствие, ухудшить экономику при обеспечении необходимого уровня надежности.
Колебания естественны для каждой энергосистемы и возникают вследствие малых изменений нагрузки в системе и возмущений, таких как отключения генераторов или линий. В целях повышения управляемости энергосистем внедряется новое оборудование, оснащенное современными быстродействующими устройствами регулирования: асинхронизированные синхронные генераторы, накопители энергии и др. В результате энергосистема приобретает новые свойства, в том числе и некоторые негативные, проявляющиеся, в частности, в возникновении низкочастотных колебаний ее режимных параметров. Влияние изменения нагрузки, составляющего небольшую долю от потока мощности, может оказаться неодинаковым для устойчивых колебаний, которые являются приемлемыми, и неустойчивых колебаний, развитие которых может привести к системной аварии. Увеличение передачи мощности на большие расстояния ведет к тому, что межзональные колебания становятся слабозатухающими или даже опасными. Уровень затухания колебаний в энергосистеме обычно зависит от активного управления при помощи системных регуляторов, установленных у генераторов, и может существенно меняться в зависимости от текущих характеристик генератора и нагрузки. При анализе результатов измерений затухания часто выявляются периоды, в течение которых затухание колебаний является слабым. Слабое затухание означает, что система может оказаться ненадежной, так как нет уверенности в том, что динамический отклик на последующие события будет устойчивым. Такую ситуацию нельзя точно отобразить в рамках динамической модели системы. Поэтому контроль затухания на основе измерений важен для предотвращения потенциальных угроз надежности, прежде чем они будут способствовать развитию крупного возмущения.
Пример. Рассмотрим свободные колебания, пусть дано ![]()
Напишем соответствующее характеристическое уравнение и найдем его корни: ![]()
1) Пусть ![]() . Тогда корни
. Тогда корни ![]() и
и ![]() - действительные отрицательные цичла. Общее решение выражается через показательные функции:
- действительные отрицательные цичла. Общее решение выражается через показательные функции:
![]() . (1)
. (1)
Из этой формулы следует, что отклонение y при любых начальных условиях асимптотически стремится к нулю, если t⟶∞. В данном случае колебаний не будет, так как силы сопротивления велики по сравнению с коэффициентом жесткости рессоры k.
2) Пусть ![]() тогда корни
тогда корни![]() и
и ![]() равны между собой (и равны отрицательному числу
равны между собой (и равны отрицательному числу ![]() ) . Поэтому общее решение будет:
) . Поэтому общее решение будет:
![]() (2)
(2)
Здесь отклонение также стремиться к нулю при t⟶∞, однако не так быстро, как предыдущем случае (благодаря наличию сомножителя ![]() ).
).
3) Пусть р=0, т.е. отсутствует сила сопротивления. Характеристическое уравнение имеет вид: ![]() а его корни равны
а его корни равны ![]() . общее решение:
. общее решение:
![]() (3)
(3)
В последней формуле произвольные постоянные ![]() и
и ![]() заменим другими. Именно, введем постоянные
заменим другими. Именно, введем постоянные ![]() и
и ![]() связанные с
связанные с ![]() и
и ![]() соотношениями:
соотношениями:
![]()
![]() и
и ![]() через
через ![]() и
и ![]() определяются так:
определяются так: ![]()
Подставляя значения ![]() в формулу (3), будем иметь:
в формулу (3), будем иметь:
![]() или
или ![]() (3')
(3')
Колебания в этом случае называются гармоническими. Интегральными кривыми являются синусоиды. Промежуток времени Т, за который аргумент синуса изменяется на ![]() , называется периодом колебаний; в данном случае
, называется периодом колебаний; в данном случае ![]() . Частотой колебания называется число колебаний за время
. Частотой колебания называется число колебаний за время ![]() ; в данном случае частота равна
; в данном случае частота равна ![]() А - величина наибольшего отклонения от положения равновесия называется амплитудой колебания;
А - величина наибольшего отклонения от положения равновесия называется амплитудой колебания; ![]() называется начальной фазой. График функции (3') на рисунке 1.
называется начальной фазой. График функции (3') на рисунке 1.
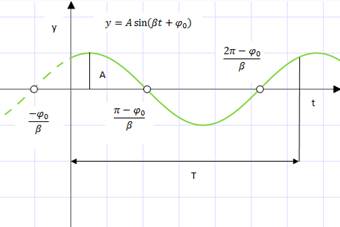
Рисунок 1. График гармонических колебаний
4) Пусть ![]() . В этом случае корни характеристического уравнения - комплексные числа:
. В этом случае корни характеристического уравнения - комплексные числа: ![]() , где
, где ![]() .
.
Общий интеграл имеет вид
![]() (4)
(4)
или
![]() (4')
(4')
Здесь в качестве амплитуды приходится рассматривать величину![]() , зависящую от времени. Так как
, зависящую от времени. Так как ![]() то она стремится к нулю при
то она стремится к нулю при ![]() т.е. здесь мы имеем дело с затухающими колебаниями. График затухающих колебаний изображен на рисунке 2.
т.е. здесь мы имеем дело с затухающими колебаниями. График затухающих колебаний изображен на рисунке 2.

Рисунок 2. График затухающих колебаний
Условия возникновения свободных колебаний можно проследить на примере пружинного маятника. Такой маятник представляет собой груз, подвешенный на пружине.
В положении равновесия пружина немного растянута, компенсируя вес груза (либо не имеет растяжения, если маятник горизонтален). При выведении из положения равновесия, в пружине возникает сила, тем большая, чем сильнее отклонение, и груз начнет движение.
Однако, в момент достижения точки равновесия, груз будет иметь некоторую скорость и кинетическую энергию. Остановиться здесь он не сможет. Он продолжит движение дальше, замедляясь и создавая в пружине новое напряжение, направленное в сторону, противоположную отклонению. В момент, когда он остановится – пружина вновь будет сжата, и снова начнет толкать груз к положению равновесия.
Таким образом, мы видим три условия, необходимых для возникновения свободных колебаний:
- система должна быть выведена из равновесия;
- при отклонениях должна возникать сила, стремящаяся возвратить систему в равновесие;
- положение равновесия должно быть единственным.
Есть еще одно, менее очевидное условие. Если пружинный маятник окажется в сильновязкой жидкости, то даже если вывести его из положения равновесия, груз медленно вернется в равновесие, и колебания не возникнут. Причина в том, что энергия сжатой пружины будет истрачена не на разгон груза, а на преодоление сопротивления вязкой жидкости.
Таким образом, последнее условие возникновения свободных колебаний – потери в системе должны быть достаточно малы, чтобы энергия, возвращающая систему в положение равновесия, терялась медленно. Примерами свободных колебаний является не только пружинный маятник, но и обычный маятник (качели), часовой балансир, натянутая звенящая струна, прыгающий мяч и многое другое.





