Усилия и моменты в составных конических куполах
Секция: Технические науки

V Студенческая международная научно-практическая конференция «Технические и математические науки. Студенческий научный форум»
Усилия и моменты в составных конических куполах
Составные конические купола из сборного железобетона встречаются в практике строительства. Примером может служить оболочка, изображенная на рис.1. представляющая систему связанных между собой усеченных многогранных пирамид, которые при расчете заменяются совокупностью конических оболочек [1].
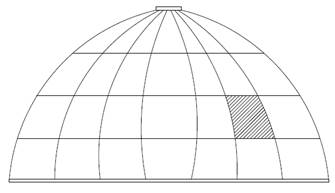
Рисунок 1.Членение оболочки вращения на сборные элементы
В местах скачкообразного изменения кривизны поверхности возникает изгибное напряженное состояние. Поэтому в сопряжениях конических оболочек должны выявляться узловые изгибающие моменты меридионального направления и горизонтальные распоры.
На рис.2,а. изображена в разрезе конструктивная схема сборного купола. В промежуточных узлах сопрягаются три конструктивных элемента: две конические оболочки вращения (сверху и снизу) и кольцо, образованное поперечными ребрами двух ярусов. В самих ребрах кольцевые изгибающие моменты невелики (поскольку малы размеры их поперечного сечения) и могут не учитываться.
Расчет промежуточных узлов целесообразно вести методом перемещений, поскольку число неизвестных величин при этом меньше.
На каждый узел накладываются две связи против перемещений: горизонтальных радиальных и меридиональных угловых (рис.2,б). В реальных конструкциях сборных куполов неизвестные усилия даже соседних узлов оказывают незначительное влияние друг на друга. Поэтому задача расчета купола сводится к расчету отдельных узлов. Впрочем, допустимость раздельного расчета узлов следует проверять каждый раз, вычисляя упругую характеристику жесткости конических ярусов оболочки. Если λ=l/s˃2 (l – длина образующей конуса, s – его упругая характеристика, определяемая по формуле:
![]()
можно взаимное влияние узлов не учитывать.
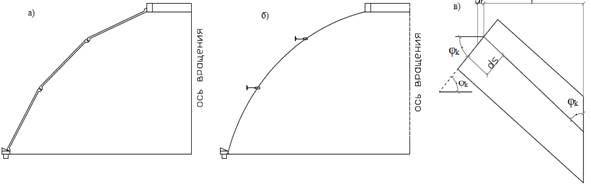
Рисунок 2. Составной конический купол из сборных плоских трапециевидных элементов (а – конструктивная схема; б – расчетная система; в – геометрические параметры конического яруса)
Крайние узлы (опорного и фонарного колец) могут рассчитываться также самостоятельно, в частности методом сил [2].
Если сборные элементы куполов имеют промежуточные ребра, то при расчете в кольцевом направлении следует пользоваться приведенной толщиной ![]() оболочки, учитывающей площадь сечения промежуточных кольцевых ребер, а в меридиональном направлении – приведенной толщиной и приведенным моментом инерции на единицу длины кольцевого сечения оболочки с учетом всех меридиональных ребер и бетона в швах между ними.
оболочки, учитывающей площадь сечения промежуточных кольцевых ребер, а в меридиональном направлении – приведенной толщиной и приведенным моментом инерции на единицу длины кольцевого сечения оболочки с учетом всех меридиональных ребер и бетона в швах между ними.
Соответственно основной системе узла (рис.3) подлежат определению угол поворота Z1 и радиальное смещение Z2 узла, для чего составляются конические уравнения:
![]() ;
;
![]() ,
,
При единичном угловом перемещении Z1=1 реакции в связях равны:
![]() ;
;
![]() .
.
Где индексами «в» и «н» помечены величины, относящиеся соответственно к верхнему и нижнему конусам оболочки.
Величины в этих выражениях определим из рассмотрения конусной оболочки с граничными условиями: при φ=0 должно быть θ=dw/dx=1 w=0. Воспользовавшись этими условиями найдем значения постоянных С1=2D/s и С2=0. Имея в виду, что Q=Hsinφk, получим:
![]() 2D/s;
2D/s;
![]() 2D/(s2sin φk),
2D/(s2sin φk),
При единичном радиальном смещении Z2=1 реакция в связи против горизонтального перемещения

Рисунок 3. К расчету промежуточного узла сборного купола при воздействии (а – единичного углового перемещения; б – единичного радиального перемещения; в – нагрузки )
![]()
Граничные условия конуса в этом случае: при φ=0 должно быть ξ=- 1 и dw/dx=0. Имея в виду, что ξ=wsinφk, находим:
С1= С2=![]() 2D/(s2sin2 φk),
2D/(s2sin2 φk),
На основании уравнения:
![]() ,
,
Учитывая, что Q= Hsinφk, имеем
![]() 4D/(s3sin2 φk).
4D/(s3sin2 φk).
Реактивный распор кольца при единичном радиальном смещении, очевидно, равен:
![]() ,
,
![]() - площадь поперечного сечения кольца.
- площадь поперечного сечения кольца.
Реакцию ![]() не вычисляем, поскольку
не вычисляем, поскольку ![]() .
.
Свободные члены в канонических уравнениях определяются следующим образом:
![]() ;
;
![]() .
.
Определим контурные усилия на краях защемленного конуса при нагрузке от собственного веса g и снега p; угловые и радиальные перемещения купола при статически определимом его опирании, вызываемые нагрузкой, сопоставим с соответствующими перемещениями при контурных воздействиях на купол момента М0 и распора Н0.
Сравним радиальные перемещения от нагрузки и от краевого воздействия при φ=φk и φk=0, имея в виду что ξ= wsinφk:
![]()
Отсюда:
![]() .
.
Сравним теперь угловые перемещения от нагрузки и от краевого воздействия, принимая в них φ=φk и φ=0:
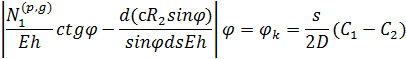
Из этого выражения:
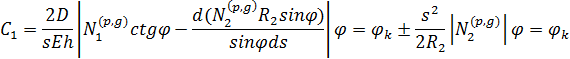
Учтем соотношения
![]()
тогда:
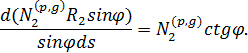
Принимая во внимание равенство, записываем выражение в виде
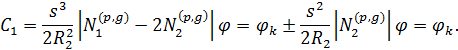
![]()
![]()
Где: ![]() – равнодействующая всех вертикальных нагрузок, находящихся выше рассматриваемого уровня.
– равнодействующая всех вертикальных нагрузок, находящихся выше рассматриваемого уровня.
При Н0=Q0/![]() и
и ![]() имеем:
имеем:
![]()
Полученные ![]() и
и ![]()
![]()
Найдя из решения систему уравнения перемещения Z1 и Z2, вычисляем окончательные значения краевых моментов и распоров по формулам:
![]()
![]()
Подставляя в них поочередно значения для верхней и нижней конических оболочек.
Распор кольца: ![]()
После раскрытия статической неопределимости узлов определяются меридиональные моменты и кольцевые усилия в конусах оболочки [3].
В составных конических куполах изгибающие моменты в меридиональном направлении охватывают всю область оболочки.





