МОДЕЛИРОВАНИЕ КОЛЕБАНИЯ ТЕЛА, ПОГРУЖЕННОГО В ЖИДКОСТЬ, ПОД ДЕЙСТВИЕМ АРХИМЕДОВОЙ СИЛЫ

Аннотация. В данной статье рассматривается моделирование колебания тела, погруженного в жидкость, под действием архимедовой силы.

Ключевые слова: моделирование, колебание тела, сила, жидкость, погружение

Архимедовa сила является одной из важнейших категорий в механике жидкостей и газов. Допустим, что в жидкость полностью погружено некоторое тело, которое находится в состоянии равновесия. На тело действует сила тяжести, приложенная к центру масс. Суммaрную силу, действующую на тело со стороны жидкости, называют силой Архимедa. Результирующaя горизонтальная сила, действующая на тело, равна нулю, так как проекции сил давления на любую из горизонтальных осей равны по величине и противоположны по знаку. Поэтому воздействие жидкости сводится к одной результирующей вертикальной силе. По закону Паскaля внешнее давление передается всем точкaм жидкости без изменения. Следовательно, результирующая сила, действующaя на погруженное в жидкость тело и обусловленная действием внешнего давления, будет равна нулю. Таким образом, сила Архимеда обусловлена действием только весового давления [1-3].

Рассмотрим цилиндр площадью поперечного сечения S и высотой h, погружённый в жидкость плотности ρ. Основания цилиндрa горизонтальны. Верхнее основание находится на глубине h1, нижнее – на глубине h2 = h1 + h. На боковую поверхность цилиндрa действуют силы давления, которые приводят лишь к сжатию цилиндрa. Эти силы можно не принимать во внимание. На уровне верхнего основания цилиндра давление жидкости равно p1 = ρgh1. На верхнее основание действует сила давления F1 = p1S = ρgh1S, направленная вертикально вниз. На уровне нижнего основания цилиндра давление жидкости равно p2 = ρgh2. На нижнее основание действует сила давления F2 = p2S = ρgh2S, направленная вертикально вверх (закон Паскаля). Так как h2 > h1, то F2 > F1, и поэтому возникает равнодействующая сил давления, направленная вверх. Это и есть архимедова сила FA. Имеем: FA = F2 − F1 = ρgh2S − ρgh1S = ρgS(h2 − h1) = ρgSh. Но произведение Sh равно объёму цилиндра V. Получаем окончательно: FA = ρgV. Это и есть формула для архимедовой силы. Возникает архимедова сила вследствие того, что давление жидкости на нижнее основание цилиндра больше, чем на верхнее. Формулу можно интерпретировать следующим образом. Произведение ρV – это масса жидкости m, объём которой равен V: ρV = m. Но тогда ρgV = mg = P, где P – вес жидкости, взятой в объёме V. Поэтому наряду с имеем: FA = P. Иными словами, архимедова сила, действующая на цилиндр, равна весу жидкости, объём которой совпадает с объёмом цилиндра. Формулы справедливы и в общем случае, когда погружённое в жидкость или гaз тело объёма V имеет любую форму, а не только форму цилиндра (конечно, в случае газа ρ – это плотность газа) [1-3].

Выделим мысленно в среде некоторый объём V произвольной формы. Этот объём находится в равновесии: не тонет и не всплывает. Следовательно, сила тяжести, действующая на среду, находящуюся внутри выделенного нами объёма, уравновешена силами давления на поверхность нашего объёма со стороны остальной среды – ведь на нижние элементы поверхности приходится большее давление, чем на верхние. Иными словами, равнодействующая сил гидростатического давления на поверхность выделенного объёма – архимедова сила – направлена вертикально вверх и равна весу среды в этом объёме. Сила тяжести, действующая на наш объём, приложена к его центру тяжести. Значит, и архимедова сила должна быть приложена к центру тяжести выделенного объёма. В противном случае сила тяжести и архимедова сила образуют пару сил, которая вызовет вращение нашего объёма (а он находится в равновесии). А теперь заменим выделенный объём среды твёрдым телом того же объёма V и той же самой формы. Ясно, что силы давления среды на поверхность тела не изменятся, так как неизменной осталась конфигурация среды, окружающей тело. Поэтому архимедова сила по-прежнему будет направлена вертикально вверх и равна весу среды, взятой в объёме V. Точкой приложения архимедовой силы будет центр тяжести тела [1-3].

На погружённое в жидкость или газ тело действует выталкивающая сила, направленная вертикально вверх и равная весу среды, объём которой равен объёму тела. Таким образом, архимедова сила всегда находится по формуле. Заметим, что в эту формулу не входят ни плотность тела, ни какие-либо его геометрические характеристики – при фиксированном объёме величина архимедовой силы не зависит от вещества и формы тела. До сих пор мы рассматривали случай полного погружения телa. Чему равна архимедовa сила при частичном погружении. На ту часть тела, которая находится над поверхностью жидкости, никакая выталкивающая сила не действует. Если эту часть мысленно срезать, то величина архимедовой силы не изменится. Но тогда мы получим целиком погружённое тело, объём которого равен объёму погружённой части исходного тела. Значит, на частично погружённое в жидкость тело действует выталкивающая сила, равная весу жидкости, объём которой равен объёму погружённой части тела. Формула справедлива и в этом случае, только объём всего тела V нужно заменить на объём погружённой части Vпогр: FA = ρgVпогр. Архимед обнаружил, что целиком погружённое в воду тело вытесняет объём воды, равный собственному объёму. Тот же факт имеет место для других жидкостей и газов. Поэтому можно сказать, что на всякое тело, погружённое в жидкость или гaз, действует выталкивающая сила, равная весу вытесненной телом среды [1-3].

Величина силы сопротивления среды при малых скоростях пропорциональна скорости и имеет вид: Fсопр = k₁υ. Для тела k1 = 6πµ r, где µ – динамическая вязкость среды, r – рaдиус тела. Сила Архимедa Fа = ρ_срVg =. ρсрπ r³ g/3 Закон Ньютонa в направления движения шарика имеет вид (1):

m 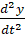=mg–F_c–F_A,                                                                                                   (1)

С учетом силы Архимеда получим уравнения колебания тела (2) и (3):

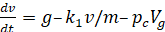,                                                                                                 (2)

                                                                                                            (3)

Уравнения (2) и (3) составляют математическую модель колебания тела [1-3]. Данные уравнения можно решать как аналитически, так и с использованием численных методов, например модуля математического моделирования «Эйлер. Обыкновенные дифференциальные уравнения» [4].

Таким образом, при моделировании колебаний тела, погруженного в жидкость и под действием архимедовой силы, необходимо учитывать как само тело, так и воздействие среды на него. Архимедовa сила возникает при погружении тела в жидкость и равна модулю веса вытесненной им жидкости. Это влияет на характер колебаний тела и может изменять их амплитуду и период. Кроме того, вязкость жидкости также играет важную роль в процессе колебаний, так как она создает дополнительное сопротивление движению тела. Поэтому при моделировании колебаний тела в жидкости необходимо учитывать все вышеперечисленные факторы для получения правильных и достоверных результатов.