НЕЧЁТКАЯ СИСТЕМА МАМДАНИ В ЗАДАЧАХ АППРОКСИМАЦИИ ФУНКЦИЙ

Аннотация. Система Мамдани – это один из методов нечеткой логики, который используется для моделирования нечетких систем и принятия решений на основе нечетких правил. Она была разработана профессором Лотфи Заде в 1975 году и с тех пор нашла широкое применение в различных областях, таких как управление процессами, искусственный интеллект, робототехника и другие.

В данной статье будет рассмотрено принципы работы системы Мамдани, её основные компоненты - нечеткие множества, лингвистические переменные, база правил и механизм вывода. Также будет рассмотрено как система Мамдани применяется для решения конкретных задач, какие у неё преимущества и недостатки.

Ключевые слова: система Мамдани, аппроксимация, нечёткая логика, множество, входная переменная.

Прежде чем перейти к самой системе, мы ознакомимся с определениями и основными понятиями нечёткой логики. Нечёткое множество (fuzzy set) – это совокупность элементов произвольной природы, о которых нельзя утверждать, к какому множеству принадлежит тот или иной элемент из рассматриваемой совокупности элементов. Нечёткая переменная определяется как кортеж: 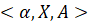, где 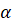 – наименование или название нечёткой переменной; Х – область её определения (универсум);  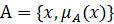– нечёткое множество Х, описывающее возможные значения, которые может принимать нечёткая переменная 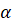. Таким образом, говоря о нечёткой переменной , мы всегда будем иметь в виду некоторое нечёткое множество А, которое определяет её возможные значения.

Одним из первых алгоритмов для систем нечёткого вывода является алгоритм Мамдани. В 1975 году английский математик Ибрагим Мамдани на основе алгебры Заде спроектировал контроллер, который управлял паровой турбиной. Согласно FAT-теореме, доказанной Бартом Каско в 1993 году, любая математическая система может быть аппроксимирована системой, основанной на нечёткой логике. Алгоритм Мамдани включает в себя несколько этапов, таких как, формирование базы правил систем нечёткого вывода, фаззификация входных переменных, агрегирование подусловий в нечётких правилах продукций, активизация подзаключений в нечётких правилах продукций, аккумуляция заключений нечётких правил продукций, дефаззификация выходных переменных.

Теперь же, на основе изученных определений, проведём тестирование нечёткой системы. Для наглядности решим следующую задачу: показать на графике зависимость выполнения тестирования от комнатной температуры и ограниченности времени.  Для начала открываем программу Fuzzy Logic в MATLAB. Определяем первую входную переменную «Время» и задаём нечёткие множества «мало», «ограничено», «много» (Рис.1).

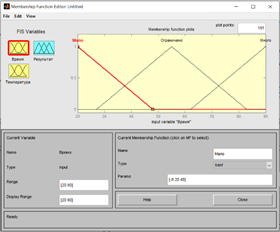
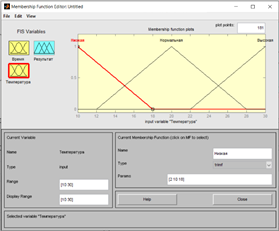
Рисунок 1.   Пример                     Рисунок 2. Пример

Определяем вторую входную переменную «Комнатная температура» и задаём нечёткие множества «низкая», «нормальная», «высокая» (Рис. 2).

Определяем выходные данные «Результат» и задаём нечёткие множества «очень плохой», «плохой», «хороший», «очень хороший» (Рис. 3).

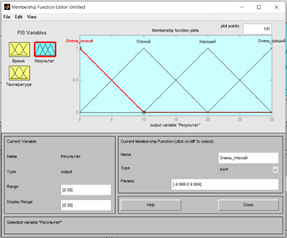
Рисунок. 3 Пример                         Рисунок 4.  Пример

Создаём базу правил, определяющую логику нечёткой системы (Рис. 4)

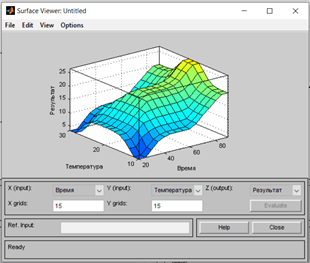
Рисунок 5. Пример

Тестирование и моделирование показало нам на графике (Рис. 5) зависимость результата тестирования от комнатной температуры и времени, которое было дано на выполнение данного теста. Таким образом, для успешного выполнения тестирования важно обеспечить комфортные условия в помещении, поддерживать оптимальную температуру и предоставить учащимся достаточно времени для выполнения заданий.

Итак, в данной статье мы рассмотрели задачу, которую с лёгкостью решила система Мамдани, данный пример раскрывает положительные стороны данного алгоритма и доказывает нам её актуальность. Система Мамдани, благодаря способности моделировать сложные и нечёткие взаимосвязи между входными и выходными переменными, может эффективно решать задачи, которые требуют работы с нечёткими данными. Данная система остаётся востребованной в современном мире благодаря своей гибкости и простоте и применяется в различных областях нашей жизни, таких как управление процессами, искусственный интеллект, медицина и экономика.