Построение и исследование частотной хеш-функции для поиска в массивах со специальной структурой

DESIGN AND RESEARCH OF THE FREQUENCY HASH FUNCTION TO SEARCH IN THE ARRAYS WITH SPECIAL STRUCTURES

Tulegen Nuryshov

master student, Faculty of Mechanics and Mathematics, Department of Information Systems, Al-Farabi Kazakh National University, Almaty, Republic of Kazakhstan

Аннотация. Локально-чувствительное хеширование (ЛЧХ) – вероятностный метод выполнения сокращения измерения высоко-размерных данных.  Однако для данного метода нужна большая память и долгая продолжительность обработки в крупном наборе данных. Кроме того, это не эффективно при расположении подобных данных в очень высоко-размерном наборе данных. Чтобы исправить возникшую проблему, будет рассмотрена новая основанная на ЛЧХ схема поиска близких объектов, которая является объединением Схема-1 последовательной хеш-функцией и Минимальной независимой перестановкой в ЛЧХ (СМЛЧХ).

Abstract. Locality Sensitive Hashing (LSH) is a method of performing probabilitic dimension reduction of highdimensional data. However, it needs large memory space and long processing time in a massive dataset. In addition, it is not effective on locating similar data in a very high-dimensional dataset. To address the problems, then a new LSHbased similarity searching scheme will be proposed that intelligently combines SHA-1 consistent hash function and Minwise independent permutation into LSH (SMLSH).

Ключевые слова: Локально чувствительное хеширование, высоко-размерный набор данных, поиск подобия, Минимально независимая перестановка.

Keywords: Locality sensitive hashing, Highdimensional dataset, Similarity searching, Min-Wise permutations.

Хеширование - общий подход, чтобы облегчить поиск подобия в высоко-размерных базах данных, и спектральное хеширование [1] является одной современной работой для хеширования данных. Спектральное хеширование применяет машину изучение методов, чтобы минимизировать семантическую потерю вложенных хешированных данных. Однако недостаток Спектрального хеширования находится в его ограниченной применимости. Поскольку спектральное хеширование полагается на Евклидовое расстояние, чтобы измерить подобие между двумя данными записями, и это требует, чтобы точки данных были из Евклидово пространства и однородно распределены.

ЛЧХ - метод сокращения размерности измерения, который преобразовывают проекты в высоко-размерном пространстве в более низко-размерное пространство, все еще сохраняя родственные связи и расстояния среди объектов. Различные семейства ЛЧХ могут использоваться для различных функций расстояния.

ОПРЕДЕЛЕНИЕ 1. Семейство H = {h: S → U} называется (r1, r2, p1, p2) чувствительной для D, если для любой точки v, q принадлежит S

• Если v ∈ B (q, r1), то Pr(H) [h (q) = h (v)] ≥ p1,

• Если v ⊈ B (q, r2), то Pr(H) [h (q) = h (v)] ≤ p2,

где r1, r2, p1, p2 удовлетворяют p1 < p2 и r1 < r2.

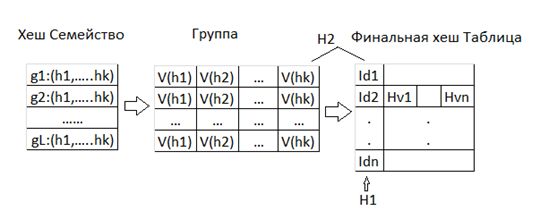
Рисунок 1: Процесс ЛЧХ

На основе ЛЧХ на p-stable распределения [3], мы строим метод поиска подобия. В рисунке 1 нарисован процесс ЛЧХ. Семейство функции хеширования ЛЧХ имеет L группы функций функции и каждая группу имеет k функции хеширования. По заданным записям данных, применяется ЛЧХ хеш-функция к записям, чтобы сформировать L групп и каждая группа имеет k значений хеширования. ЛЧХ использует H1 хеш-функцию на k хеш-значениях каждой группы, чтобы произвести индексирование местоположения записей в заключительной хеш-таблице и использует H2 хеш-функцию на k хеш-значениях каждой группы, чтобы вычислить значение записи, и сохранить в памяти. Наконец, у записи есть L значений, сохраненных в заключительной хеш-таблице. Учитывая запрос, ЛЧХ использует тот же самый процесс, чтобы произвести L-индексирование и значений запроса, и находит подобные записи на основе индексов, и определяют заключительные подобные записи на основе сохраненных значений.

Бродер и др. [2] определили что, F ⊆ Sn является минимальной независимой перестановкой, если для любого множества X ⊆ [n] и x ⊆ X, случайно выбранным π из F,

Pr (min {π (X)} = π (x)) = ,

где Pr является вероятностью. Все элементы любого зафиксированного множества X имеют равный шанс стать минимальным элементом X под π.

В [2], семейство функций хеширования F является семейством функции ЛЧХ функции подобия sim(A, B), если для всех h ∈ F воздействующих на два набора A и B, мы имеем:

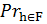 [h (A) = h (B)] = sim (A, B), где sim (A, B) ∈ [0, 1] является функцией подобия.

Минимальная независимая перестановка обеспечивают индекс Джаккарда, чтобы оценить подобность:

sim (A, B) =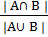 

Например, U = {a, b, c, d, e, f}, S = {a, b, c}, S′ = {b, c, d}, и S ⊂ U и S′ ⊂ U. Случайная перестановка π множества U является π = <d, f, b, e,  a,  c>. Поскольку b содержится в S, и является первым элементом в π, b является минимальным изображением S под π, обозначим как b = min {π (S)}. Поскольку d содержится в S′ и является первым элементом в π, d является минимальным изображением S под π, обозначим как d = min {π (S)}.

S ∩ S′ = {b, c} и S ∪ S′ = {a, b, c, d}. Для случайной перестановки множества U: π (U) = {e, p1, p2, f, p3, p4},

где p1, p2, p3 и p4 может быть a, b, c и d в любом порядке, если p1 из {b, c}, то min {π (S)} =min {π (S′)}, и S и S′ подобны.

Из следующих равенств:

Pr (min {π (S)} = min {π (S′)}) = 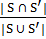 =| {b, c} | ,

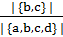мы можем определить подобие между S и S′.

Итак, СМЛЧХ уменьшает ложно-положительные результаты и между тем уменьшает память для записей и хеш-таблиц. Метод не требует, чтобы  все записи были одной и той же размерности. Таким образом, вектор каждой записи имеет размерность, которая не равна размерности объединенного многомерного пространство, состоящее из ключевых слов.

Записи в базах данных обычно задаются в текстовом формате. Поэтому оригинальная запись данных может быть не использована при вычислениях. Чтобы произвести идентификатор для каждого ключевого слова в записи  СМЛЧХ сначала использует Схема-1 последовательные функции хеширования. Схема предназначена для Безопасного Алгоритма Хеширования, которая включает пять шифровальных функции хеширования. Схема-1 - хеш-функция, которая является одной из пяти шифровальных функций хеширования, используется в нескольких широко используемых программах безопасности и протоколах, таких как TLS, SSL и IPsec . Хеш-функция Схема-1 стойкая к коллизии, таким образом, она может использоваться при хешировании ключевых слов в целые числа. СМЛЧХ сначала изменяет все ключевые слова на прописные буквы. Как показано ниже, после изменения все ключевые слова записи - заглавные буквы, СМЛЧХ использует Схему-1, чтобы хешировать все ключевые слова заглавной буквы в ряд целых чисел:

Колпаков СЕРГЕЙ Андреевич Москва 1331

Заглавная запись: КОЛПАКОВ СЕРГЕЙ АНДРЕЕВИЧ МОСКВА 1331

Хеш-запись: 1945773335 628111516 2140641940 2015065058 125729831

ЛЧХ требует, чтобы у всех векторов записей было одинаковая размерность, чтобы построить группы с универсальной хеш-функцией. В ЛЧХ, длина вектора каждой записи равняется длине списка ключевых слов, состоящего из всех ключевых слов в наборе данных. Напротив, СМЛЧХ не требуют, чтобы у всех записей была одна и та же размерность. В СМЛЧХ длина вектора записи равна количеству ключевых слов самой записи. Таким образом, СМЛЧХ уменьшает памятьо ЛЧХ для векторов. В СМЛЧХ,  минимальная независимая перестановка определена как:

π (x) = (ax + b) mod prime, где a и b - случайные целые числа, 0 ≤ a ≤ prime и 0 ≤ b ≤ prime, где prime – простое число.

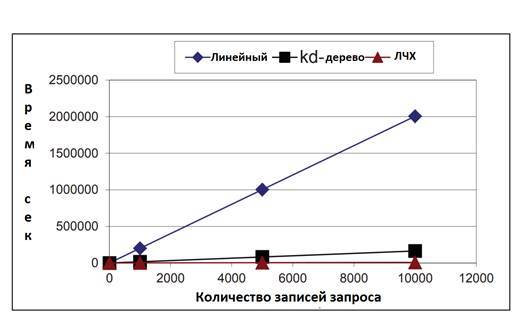
Рисунок 2. Время запроса в линейном, kd-дерево и ЛЧХ поиске

Рисунок 2 показывает время выполнения запроса поисковых методов на основе линейного метода, kd-дерева и ЛЧХ соответственно. В линейном методе запрос сравнивается с каждой записью в наборе данных в поиске данных. Как и ожидалось, время выполнения запроса линейного метода поиска является самым высоким, и ЛЧХ приводит к более быстрому подобному местоположению записей, чем метод kd-дерева.

Рисунок 3. Место памяти для исходных записей и хеш-таблиц

Рисунок 3 демонстрирует, что потребление памяти и для преобразованных исходных записей и для хеш-таблиц в СМЛЧХ намного меньше, чем в ЛЧХ. Это происходит из-за того, что у СМЛЧХ векторы записей намного короче, и, следовательно, требуется меньше памяти хранения.