Визуализация графиков с использованием программы Gnuplot
Секция: Технические науки

XL Студенческая международная заочная научно-практическая конференция «Молодежный научный форум: технические и математические науки»
Визуализация графиков с использованием программы Gnuplot
Gnuplot − это терминальная программа, которая запускается из командной строки (существуют также графические интерфейсы gui) и работает под управлением ОС Linux, Windows и Mac OS X.
Управление работой программы осуществляется с помощью специальных команд, вводимых либо с клавиатуры, либо из специального текстового файла. Программа может строить 2-х и 3-х мерные графики, графики в полярных координатах, специальные статистические графики с показанным отклонением, столбчатые диаграммы и многое другое. Слабое место − это построение круговых диаграмм. Их построение требует написания довольно сложных команд. Программа позволяет автоматически подбирать параметры формульных зависимостей, наилучшим образом приближающие экспериментальные данные. Имеется возможность работать с «календарными» переменными, определяющими дату (допустимо только английские названия месяцев и дней недели). В процессе работы Gnuplot выводит на экран описание ошибки. На место ошибки снизу указывает символ ^. Для помощи пользователю имеется развитая справочная система [2].
Формально gnuplot создавался для визуализации научных данных. Есть много указаний на то, что учёные используют gnuplot, в том числе и для предоставления полученных данных. Например, климатические карты, предоставляемые NASA [1, с. 78], создаются с помощью этой программы. Gnuplot − прекрасный выбор для задач графического анализа. Его командная строка обеспечит эффективное проведение быстрых интерактивных экспериментов с данными любого сорта, от демографических тенденций до 3D-моделей.
Программу можно полностью автоматизировать, она не требует много ресурсов и может работать на сервере без графической оболочки − полезно, например, при создании графиков на суперкомпьютере с использованием больших объемов данных. Необходимые файлы данных и команды представляют собой простой текст ASCII, а графики на выходе можно экспортировать в любой формат, например, PNG, GIF, PostScript или для LaTeX.
Gnuplot может не только строить графики по уже имеющимся данным, у него есть встроенный язык программирования, схожий с «С», в котором предусмотрены множество математических функций, ветвления и циклы. За счет этого возможно предварительно обрабатывать данные, а также строить графики функции, задаваемых математическими формулами.
Выполним построение нескольких графиков в программе. Построить график функции 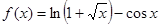 . Команды для построения графика имеют вид
. Команды для построения графика имеют вид
set key bottom
set xrange [0:10]
set xlabel "x"
set ylabel "f(x)"
plot log(1+sqrt(x))-cos(x) with lines lc 1
Где первая команда определяет легенду и размещает ее внизу графика; вторая настраивает масштаб графика от 0 до 10. Команды set xlabel "x" и set xlabel "f(x)" подписывают оси координат. Последняя команда выполняет построение графика функции. В результате получиться график представленный на рис. 1.
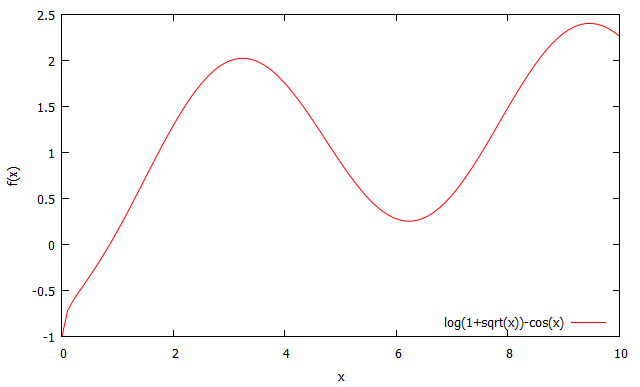
Рисунок 1. Результат построения графика функции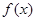
Функция заданная параметрически имеет вид
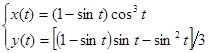
Команды для построения графика запишутся в виде
set parametric
set trange [0:2*pi]
x(t) = (1-sin(t))*cos(t)**3
y(t) = ((1-sin(t))*sin(t) – sin(t)**2)/3
plot x(t), y(t) with lines
Результат построения графика представлен на рис. 2.

Рисунок 2. Результат построения графика функции, заданной в параметрической форме
Сейчас перейдем к построению графика функции, заданной в полярной системе координат. Для построения графика в полярной системе координат необходимо определить полярную систему координат с помощью команды: set polar. При этом аргументом является переменная t. Пример построения графика функции 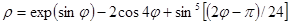 при
при  имеет вид
имеет вид
set polar
set grid polar
unset key
set samples 2000
set trange[-8*pi:8*pi]
plot exp(sin(t))-2*cos(4*t)+sin((2*t-pi)/24)**5
Полученный график представлен на рис. 5
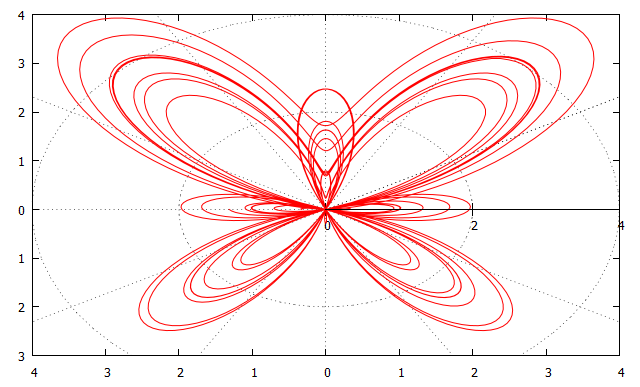
Рисунок 3. Пример построения графика в полярной системе координат
Выполняя построения графиков можно выполнять анализ функции, а именно искать ее экстремумы, минимум и максимум, а также строить производные функции.





