Быстрые алгоритмы дискретного преобразования Фурье

В работе рассматриваются быстрые алгоритмы дискретного преобразования Фурье. Данные алгоритмы позволяют снизить вычислительную сложность обычного дискретного преобразования Фурье.

Введение

Пусть v = {v_i, i = 0,..,n-1} обозначает вектор с вещественными или комплексными компонентами.

Определение. Преобразованием Фурье вектора v называется вектор V длины n с комплексными компонентами, задаваемыми равенствами

где: 

Преобразование Фурье, записанное в таком виде требует n² сложений и n² умножений. Для уменьшения количества арифметических операций рассмотрим быстрые алгоритмы преобразования Фурье.

Алгоритм Кули-Тьюки в общем виде

Для построения алгоритма предполагается, что n = n₁n₂. В выражении для преобразования Фурье произведем следующую замену записи индексов:

i = i₁ + n₁i₂                      i₁ = 0,..,n₁-1                   i₂ = 0,..,n₂-1

k = n₂k₁ + k₂           k₁ = 0,..,n₁-1                  k₂ = 0,..,n₂-1

Подставим новые обозначения в исходную формулу преобразования:

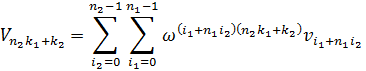
Определим двумерные переменные для удобства записи формул:

Раскроем скобки в показателе степени и положим  и  Также примем во внимание, что 

В терминах двумерных переменных формула преобразуется к виду

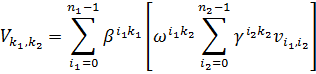
Дискретное преобразование Фурье по алгоритму Кули-Тьюки требует не более n*(n₁ + n₂ + 1) комплексных умножений и n*(n₁ + n₂ – 2) комплексных сложений. В общем случае количество умножений и сложений можно записать следующим образом:

M_C(n) = n₁M_C(n₂) + n₂M_C(n₁) + n

A_C(n) = n₁A_C(n₂) + n₂A_C(n₁)

Так, например, для n = 1000 (учитывая, что M_C(2) = 0, M_C(5) = 10):

M_C(1000) = 2M_C(500) + 500M_C(2) + 1000 = 2M_C(500) + 1000 = 11000

Таким образом, алгоритм Кули-Тьюки дает выигрыш по количеству умножений в 1000000/11000 ≈ 91 раз.

Визуально алгоритм выглядит следующим образом: значения вектора v заносятся по порядку в таблицу n₁ на n₂ слева направо, сверху вниз. Вычисления состоят из n₂-точечного ДПФ каждого столбца, поэлементного умножения всех элементов таблицы соответственно на  и n₁-точечного ДПФ для каждой строки.

Алгоритм Кули-Тьюки в случае, когда n = 2^m

Если n₁ = 2, а n₂ = 2^m-1, то алгоритм называют алгоритмом Кули-Тьюки по основанию два с прореживанием по времени. Используя тот факт, что  уравнения, задающие БПФ, можно записать в следующем виде:

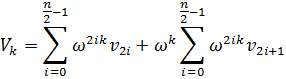
k = 0,..,n/2 – 1

Если n₁ = 2^m-1, а n₂ = 2, то алгоритм называют алгоритмом Кули-Тьюки по основанию два с прореживанием по частоте. Уравнения БПФ в этом случае преобразуются к виду:

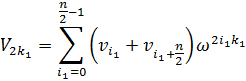
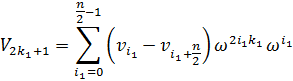
Число M_C(n) комплексных умножений n-точечного БПФ удовлетворяет уравнению M_C(n) = 2M_C(n/2) + n/2, а число A_C(n) комплексных сложений удовлетворяет уравнению A_C(n) = 2A_C(n/2) + n. Решения этих уравнений даются равенствами

M_C(n) = (n/2) log₂n,

A_C(n) = n log₂n

Алгоритм Гуда-Томаса

Для применения алгоритма Гуда-Томаса числа n₁ и n₂ должны быть взаимно простыми. В двумерную таблицу входные данные выписываются, начиная с верхнего левого угла, вдоль расширенной диагонали. Входные индексы задаются по правилу

i₁ = i (mod n₁),                i₂ = i (mod n₂)

Это правило представляет собой отображение индекса i на расширенную диагональ двумерной таблицы, элементы которой занумерованы парами индексов (i₁, i₂). Из теории чисел известно, что для чисел n₁ и n₂ существуют такие целые числа N₁ и N₂, что N₁n₁ + N₂n₂ = НОД(n₁, n₂). Если n₁ и n₂ взаимно просты, то, согласно китайской теореме об остатках

i = i₁N₂n₂ + i₂N₁n₁ (mod n).

Пусть k₁ = N₂k (mod n₁), k₂ = N₁k (mod n₂). Тогда выходные индексы вычисляются по правилу

k = n₂k₁ + n₁k₂ (mod n).

В этих новых индексных обозначениях формула преобразуется к виду

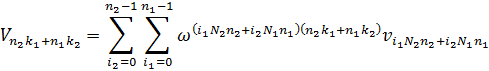
Раскроем скобки в показателе степени

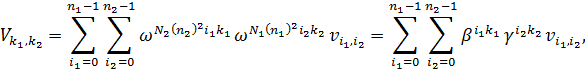
где: 

Если длина n преобразования раскладывается в произведение простых множителей n_l, то описанная форма БПФ-алгоритма требует примерно  умножений и столько же сложений. Например, для n = 1000 = 2*2*2*5*5*5 число умножений MC(1000) = 1000*(2+2+2+5+5+5) = 21000, что дает выигрыш по количеству операций умножения в 1000000/21000 ≈ 48 раз.

Заключение

В работе были рассмотрены два наиболее известных алгоритма дискретного преобразования Фурье, а также рассчитаны выигрыши по количеству умножений данных алгоритмов по сравнению с обычным алгоритмом преобразования Фурье.