Применение алгоритма K-MEANS для эскизного проектирования местоположения транспортных объектов

В данной работе мы рассмотрим алгоритм кластеризации k-means, затем внесем в него некоторые изменения, чтобы он был пригоден для решения нашей практической задачи, а именно для проектирования местоположения контейнерно-накопительных пунктов на территории железнодорожных станций.

Понятие кластеризации

Кластеризация – это задача разбиения множества объектов на группы, называемые кластерами. В нашем случае множеством объектов будут являться промышленные организации.

Для того, чтобы сравнивать два объекта, необходимо иметь критерий, на основании которого будет происходить сравнение. В рамках нашей задачи таким критерием будет являться расстояние между объектами.

Алгоритм k-means

Наиболее распространен среди неиерархических методов алгоритм k-means. Единственным управляющим параметром является число классов, на которые проводится разбиение выборки Х. В результате получается несмещенное разбиение .

Схема алгоритма:

1.  Выберем начальное разбиение где ,.

2.  Пусть построено m-е разбиение  Вычислим набор средних где .

3.  Построим минимальное дистанционное разбиение порождаемое набором  возьмем его в качестве, т.е.:

,

где: расстояние в .

4.  Если ,то переходим к п.2, заменив m на m+1, если , то полагаем S^m=S* и заканчиваем работу алгоритма.

Валидация кластеров

Под валидацией кластеров понимают проверку их обоснованности. В контексте нашей работы это означает проверку приемлемости полученных результатов по определению мест расположения контейнерных пунктов.

Наиболее популярным является индекс Дэвиса – Болдина, который можно определить следующим образом. Охарактеризуем относительный разброс в двух кластерах как полусумму средних расстояний их элементов до центров, деленную на расстояние между центрами. Охарактеризуем разброс кластера максимальной величиной его относительного разброса (относительно других кластеров) [3, с.67].

Тогда индекс Дэвиса – Болдина – не что иное, как средний разброс кластеров [2].

,

где: K – количество кластеров, S_K – среднее расстояние от объектов до центра кластера, S(Q_i,Q_j) – расстояние между центрами кластеров. Чем меньше значение этого индекса, тем кластеры компактнее и удалённее друг от друга.

Подобно индексу DB в целях нашей задачи можно в качестве критерия выбора числа кластеров рассмотреть показатель среднее от среднего расстояние от объекта до своего центра – , которое будет определять средние экономические затраты подвоза грузов к КП.

Программная реализация

Итак, исходными данными нашей задачи являются координаты и объём производства 907 предприятий Приволжского Федерального округа, а также координаты 89 железнодорожных станций.

Запустим на выполнение программу и выберем в качестве критерия суммарное расстояние от всех точек до своих центров. Результат выполнения программы представлен на рисунке 1.

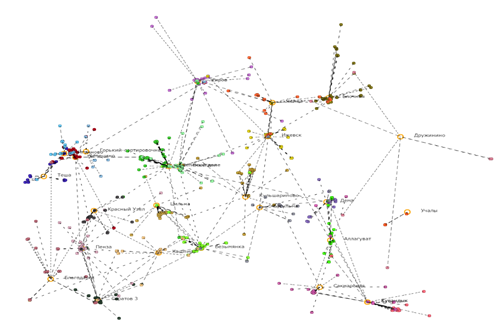
Рисунок 1. Результат выполнения программы (критерий суммарного расстояния)

График зависимости критерия (k) показан на рисунке 2.

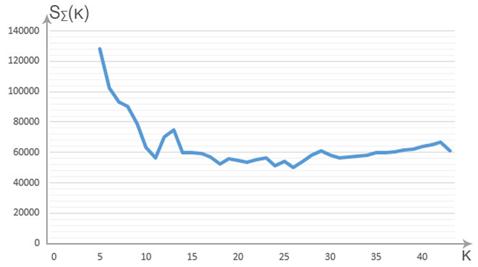
Рисунок 2. График зависимости суммарного расстояния от количества кластеров

Были получены следующие данные: количество кластеров – 26, (26) = 50195.

Затем выберем в качестве критерия индекс Дэвиса-Болдина. Результат выполнения программы представлен на рисунке 3. График зависимости критерия DB показан на рисунке 2.

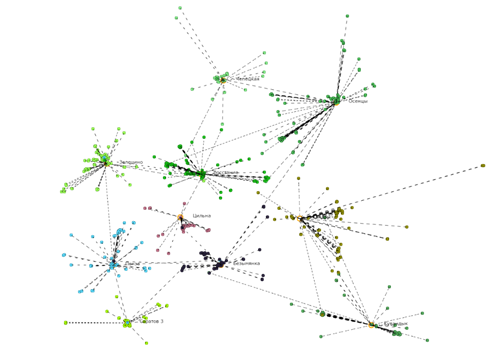
Рисунок 3. Результат выполнения программы (критерий - индекс Дэвиса-Болдина)

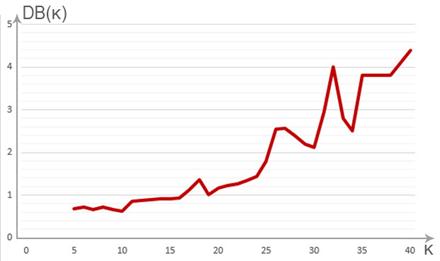
Рисунок 4. График зависимости индекса Дэвиса-Болдина от количества кластеров

Во втором случае мы получили следующие данные: количество кластеров – 10, DB = 0.63.

Заключение

Итогом нашей работы стала разработка программного продукта, который может быть использован для решения практических задач, связанных с кластеризацией объектов по критерию расстояния между ними.