Построение и обоснование микросхемы одноразрядного сумматора
Секция: Технические науки

XLII Студенческая международная заочная научно-практическая конференция «Молодежный научный форум: технические и математические науки»
Построение и обоснование микросхемы одноразрядного сумматора
Как ранее так и в настоящее время одной из актуальных задач в области Computer Science, а в нашем случае, в области архитектуры компьютера является задача синтеза и обоснования цифровых схем. Среди подобных задач важной и классической задачей является задача построения и обоснования схемы сумматора. Последний, как известно, находит применение для различных цифровых схем, в том числе и как часть АЛУ (арифметико-логического устройства), а также и для других вычислительных моделей. Каждое нововведение в области дизайна цифровых схем требует формального (математического) обоснования методами дискретной математики [3]. Так в книге [3, с. 364] представлена схема одноразрядного сумматора
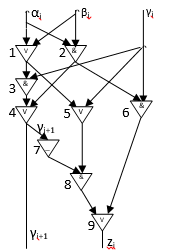
Рисунок 1.
и её обоснование в виде булевых формул для вычисления разряда суммы и разряда переноса.
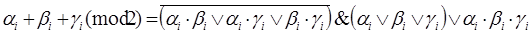
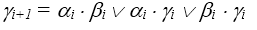
где: ![]() это первое и второе слагаемые суммы, соответственно. Значение
это первое и второе слагаемые суммы, соответственно. Значение ![]() – значение переноса в i разряд,
– значение переноса в i разряд,![]() перенос в i +1 разряд соответственно, при этом
перенос в i +1 разряд соответственно, при этом ![]() . Для блока
. Для блока ![]() и сама схема
и сама схема
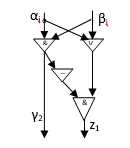
Рисунок 2.
и формулы выглядят значительно проще ( ![]()
![]()

Схема блока Рис.2. представляет собой «усеченный» вариант схемы на Рис.1.
Забыв, о том, что речь, вообще говоря, идет о 1-м разряде n –разрядного сумматора, заметим, что схема на Рис.2 является полусумматором, поскольку вырабатывая разряд суммы и разряд переноса γ, схема не учитывает перенос в текущий разряд. Попутно заметим, что схема реализует функцию XOR (выход z1). Очевидно, что число транзисторов(биполярных) схемы на Рис.2. равно 10, а вентилей 4, тогда как, для схемы на Рис.1. число вентилей равно 9 при 1<i≤n. Для n-разрядного сумматора вентильная сложность оценивается величиной:
![]()
Таким образом, сумматор, приведенный на Рис.1, обладает еще одной существенной характеристикой, а именно, глубиной, которая для данной схемы равна 6 и эта схема имеет приемлемую вентильную и транзисторную сложность. Схема сумматора на Рис.1. имеет важную дополнительную особенность, которая отличает её от некоторых других подобных схем, а именно, в этой схеме, схема переноса полностью интегрирована в схему для вычисления суммы-вентили 1, 2, 3, 4. Другой пример сумматор из книги [2, с.187], записан в «крупно-блочном» варианте и представляет собой схему, построенную на основе схемы XOR для которой в [2], не приведено формульное обоснование.
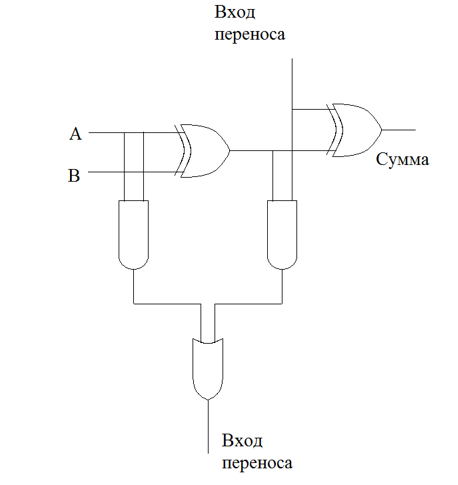
Рисунок 3.
Здесь представляет интерес задача построения схемы, на основе схемы из [2], в базисе, ![]() , давая, при этом, её формульное обоснование. Очевидно, что решение упомянутой задачи не будет однозначным, уж потому, что схема XOR допускает неоднозначную реализацию с использованием элементарных вентилей, в базисе
, давая, при этом, её формульное обоснование. Очевидно, что решение упомянутой задачи не будет однозначным, уж потому, что схема XOR допускает неоднозначную реализацию с использованием элементарных вентилей, в базисе ![]() . При этом разумеется и вентильная и транзисторная сложность схемы, а также и глубина схемы сумматора будет различной. В докладе будет дан один метод обоснования схемы, на основе схемы из [2] в базисе
. При этом разумеется и вентильная и транзисторная сложность схемы, а также и глубина схемы сумматора будет различной. В докладе будет дан один метод обоснования схемы, на основе схемы из [2] в базисе ![]() с вентильной сложностью 13, глубиной 6. Отметим, что в таком виде сумматор может быть использован как элементарный блок мультипроцессора или как элемент сумматора нейросети, а также может быть использован вычислительный элемент мультиагентной системы.
с вентильной сложностью 13, глубиной 6. Отметим, что в таком виде сумматор может быть использован как элементарный блок мультипроцессора или как элемент сумматора нейросети, а также может быть использован вычислительный элемент мультиагентной системы.





