Анализ генетических алгоритмов как инструмента оптимизации

Принятие решений в различных областях деятельности человека сопряжено с обработкой и анализом значительного объема данных. Зачастую скорость принятия такого решения имеет большое коммерческое значение и определяет эффективность развития целого направления.

Одним из методов поиска оптимального решения является использование генетических алгоритмов, основанных на генетических процессах биологических организмов, и адаптируемых к решению широкого круга практических задач, где не существует специализированных методов решения.

Генетические алгоритмы используют прямую аналогию с естественным поведением. Они работают с набором особей, каждая из которых представляет собой возможное решение проблемы. Каждой особи присваивается оценка ее пригодности в соответствии с тем, насколько хорошее решение оно представляет. Самым пригодным особям дают возможность воспроизведения путем скрещивания с другими особями набора. Это порождает новых особей как потомков, которые имеют некоторые характеристики, взятые у каждого из родителей. Наименее пригодные члены с меньшей вероятностью будут отобраны для размножения [1, с. 58].

Таким образом, создается полностью новая совокупность возможных решений путем выбора лучших особей из нынешнего поколения и объединения их для создания нового набора. Это новое поколение содержит более высокую долю характеристик, которыми обладают хорошие представители предыдущего поколения. В течение многих поколений хорошие характеристики распространяются по всему набору, будучи смешанными, и обмениваются с другими хорошими характеристиками по мере их поступления. Схема работы генетического алгоритма представлена на рис.1.

Существующие специализированные методы решения конкретных проблем, вероятно, будут превосходить генетические алгоритмы как с точки зрения скорости, так и с точностью конечного результата. Генетические алгоритмы используются в трудных областях, где таких методов не существует. Даже те методы, которые работают хорошо, возможно улучшить путем их комбинирования с принципами генетических алгоритмов.

Перед использованием генетических алгоритмов необходимо разработать подходящее кодирование или представление проблемы. Также понадобится функция “fitness”, которая присваивает каждому решению оценку его пригодности. Во время работы алгоритма должны быть отобраны родители для размножения и рекомбинированы для создания потомства [4, с. 36].

Предполагается, что потенциальное решение проблемы может быть представлено в виде набора параметров (генов), которые объединяются вместе, чтобы сформировать строку значений (хромосому) [3, с. 135].

Функция оценки пригодности (“fitness”) должна быть разработана отдельно для каждой решаемой задачи. Принимая определенную хромосому, функция возвращает числовую оценку пригодности, которая должна соответствовать полезности решения.

Во время репродуктивной фазы особи выбираются из популяции и рекомбинируются, производя потомство, которое будет включать следующее поколение. Родители выбираются случайным образом из популяции, используя схему, которая благоприятствует наиболее подходящим индивидам. Хорошие особи, вероятно, будут выбраны несколько раз, тогда как менее пригодные особи, возможно, не будут вообще. Выбрав двух родителей, их хромосомы рекомбинируют, обычно используя механизмы скрещивания и мутации.

Скрещивание делит их хромосомные строки в некотором случайно выбранном положении, чтобы произвести два головных и два конечных сегмента. Затем конечные сегменты меняются местами для получения двух новых полноразмерных хромосом. Такое скрещивание называется одноточечным (рис. 2). Мутация применяется к каждому потомку отдельно после скрещивания. Она случайным образом изменяет каждый ген с небольшой вероятностью (рис. 3).

Рисунок 1. Схема работы генетического алгоритма

Рисунок 2. Одноточечное скрещивание

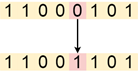
Рисунок 3. Мутация

Популяция сходится, когда доля набора имеет одно и то же значение на всех генах.

Аналогичные техники:

·     Случайный поиск. Сложность полного перебора зависит от количества всех возможных решений задачи. Если пространство решений очень велико, то полный перебор может не дать результатов в течение нескольких лет или даже столетий.

·     Алгоритм имитации отжига. Начиная с произвольной точки в пространстве поиска, происходит случайный шаг, если этот шаг ведет нас к высшей точке, он принимается, а если он ведет нас к нижней точке, он принимается только с вероятностью p(t), где t-время. В начале поиска функция принимает значение 1, но постепенно сводится к нулю. Как и случайный поиск, имитация отжига работает только с одним вариантом решения в отдельный момент времени, в то время и поэтому не выстраивает общей картины пространства поиска. Никакая информация с предыдущих ходов не учитывается при следующем ходе.

Недостатки:

·     Проблема определения функции оценки пригодности. Решающее значение в эффективности генетических алгоритмов принимает функция оценки пригодности и схема кодирования. Общим правилом построения функции оценки является то, что пригодность хромосом не должна отражаться посредством специализированных методов. К сожалению, пригодность хромосомы, рассчитанная специализированным методом, не всегда является полезной величиной для генетического поиска.

·     Проблема локального оптимума заключается в том, что гены нескольких хромосом со сравнительно высокой пригодностью, особи могут доминировать в поколении, заставляя пригодность хромосом следующего поколения приблизиться к локальному максимуму. Как только популяция сошлась, способность генетического алгоритма найти лучшие решения фактически исключена, т.к. скрещивание почти идентичных хромосом производит мало нового.

·     Проблема завершения работы алгоритма. После многих поколений, популяция в большей степени сошлась, но глобальный максимум не достигнут. Средняя стоимость пригодности поколения будет высокой и разница пригодности между лучшими и средними особями не велика.

Техники оптимизации скрещивания:

·     Двухточечное скрещивание. Двухточечное скрещивание делит хромосомные строки в двух случайно выбранных положениях. Затем двое родителей обмениваются сегментами, находящимися между этими положениями, тем самым образуя двое новых потомков. При этом строка преобразуется в петлю для корректной обработки ситуаций, когда вторая точка конца расположена ближе к началу, чем точка начала.

·     Универсальное скрещивание. В основе универсального скрещивания лежит использования маски скрещивания. Если в некотором положении ген маски принимает значение 1, то ген потомка в том же положении наследуется от первого родителя, если 0 – то второго.

Для объёмных хромосом рекомендуется использовать универсальное скрещивание т.к. оно гарантирует более распределенное скрещивание.

Генетические алгоритмы активно используются при оптимизации функций, при решении разнообразных задач на графах, задач компоновки и при настройке и обучении нейронных сетей [2, с. 1].

С целью исследования генетического алгоритма как инструмента оптимизации разработана демонстрационная программа с использованием языка С++, результат которой полностью подтвердил теоретические предположения об эффективности выбранной методики.

В качестве практической реализации для использования полученных выводов выбрана задача прогнозирования покупок в магазине, которая обеспечит возможность своевременного обновления ассортимента и повышения прибыли.

Исследование поддержано проектом CERES. Centers of Excellence for young RESearchers (Reg.no. 544137-TEMPUS-1-2013-SK-JPHES.