Комплексные числа в электротехнике

Комплексным числом z называется выражение вида , где  и  действительные числа, а  так называемая мнимая единица,  и это выражение в виде  называется алгебраической формой . мы можем обозначать , а  мнимой частью , . В электротехнике мы обозначаем . Комплексное число  можно изобразить точкой A(x;y) плоскости Oxy такой. Плоскость на которой изображаются комплексные числа, называется комплексной плоскостью.

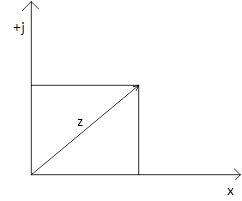
Рисунок 1. Комплексной плоскостью

Модуль |z| и аргумент α комплексная числа получаем x=|z|cosα, y=|z|sinα. Следовательно, комплексное число  можно записать в виде:

Или

                                             (1)

Такая запись (1) комплексного числа называется тригонометрической формой.

Формула Эйлера:

                                                  (2)

Изображение синусоидально изменяющихся величин векторами на комплексной плоскости. С помощью формулы Эйлера в уравнении (2), проекция функции  на ось +1 равна , а на ось +j равна . Если вместо функции  подставим функцию , то получим такое уравнение:

                                    (4)

Угол  в формуле (2) изменяется прямо пропорционально времени как показано на рисунке (3), где вместо величины  подставим  . То у нас получится такое уравнение:

                                                             (5)

Тогда  (6)

Таким образом, синусоидально изменяющийся ток  формулы (6) можно представить Im или Im .

С целью единообразия принято на комплексной плоскости изображать векторы синусоидально изменяющихся во времени величин для момента времени . При этом вектор  равен , где  называют комплексной амплитудой тока .

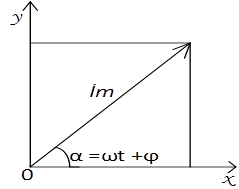
Рисунок 2.

Рассмотрим тригонометрическую функцию A(t) представленную в виде комплексной величины на комплексной плоскости.

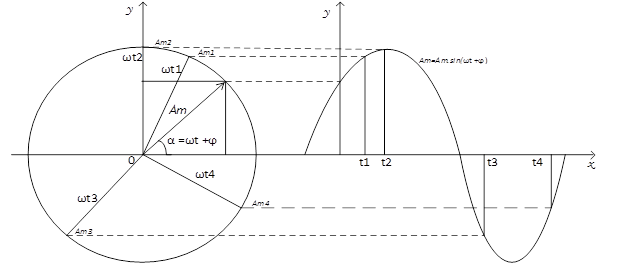
Рисунок 3. Вектор на комплексной плоскости

На рисунке (3) так как меняется угол в течении времени так и синусоидальная функция меняется также, это значит что в синусоидальная функция зависит от комплексных чисел, в электрической цепи мы видим, что ток и напряжение ведут себя как синусоидальная функция. Угол начальной фазы равен:

                                                           (7)

Между мгновенными значениями синусоидальных величин и их комплексными значениями существует взаимно однозначное соответствие. Совместное решение алгебраических уравнений, для определения комплексных значений токов и напряжений всех элементов цепи, то есть применение комплексного метода расчета, достаточно простая задача. По найденным комплексным значениям можно записать при необходимости и соответствующие им мгновенные значения синусоидальных величин.

Первый закон Кирхгофа: сумма токов узле равна нулю.

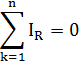
где: n – число ветвей, подключенных к узлу.

Второй закон Кирхгофа: сумма ЭДС в любом контуре электрической цепи равна сумме поденный напряжений на всех элементах этого контура.

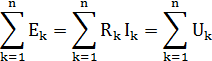
где: n – число источников ЭДС в контуре, m- число элементов с сопротивлением Rk в контуре.

Решаем один задач для синусоидально тока который показана на рисунок 4, требуються найти  , знай что С1=64.96мф и R1=18ом L1=79.58mH.

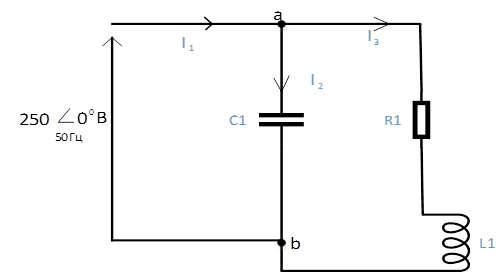
Рисунок 4. Синусоидальный ток

В цепи (рис. 4) при действии источника синусоидальной =, это выражение мы записываем в форме комплексного числа =, так мы получим =250B, ток также синусоидален:  и напряжение на резистивном, индуктивном и емкостном элементах.

Первый мы найдем  и одно сопротивление где проходит ток I3 и обозначим Zx

В формуле Эйлера можем записать Zx=30,81

Рассчитаем в ветви a-b где происходит ток I2:

В комплексной форме –jXc можем записать как Zy=49.

Получим сопротивление эквивалентное:

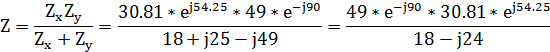
Ом

C помощью закон Ома рассчитаем электрический ток:

I2=

I3=

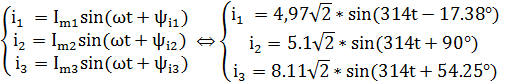
Выводы: с помощью комплексного числа это возможность обозначать синусоидальная тока на комплексной плоскость. Когда мы используем комплексные числа для расчета цепей помогает нам понимать сложней цепи. В ряды Фурье любая произвольная функция можем записать в периодических бесконечных условиях.