Обзор алгоритмов линейного и бинарного поиска

В статье рассматривается работа алгоритмов линейного и бинарного поиска, реализация алгоритмов на языке программирования C++, анализ их базовых свойств и область их применения.

Для начала рассмотрим алгоритм линейного поиска. Алгоритм линейного поиска является одним из основных и простых алгоритмов в информатике для поиска конкретных элементов на некотором множестве.

Линейный поиск выполняет поиск элемента или значения из некоторого множества до тех пор, пока нужный элемент или значение не будет найден, порядок поиска последовательный.

Сравнивается искомый элемент со всеми элементами на некотором множестве, если искомый элемент будет найден, то функция возвращает индекс найденного элемента, в противном случае функция возвращает -1. Линейный поиск применяется к неотсортированному или неупорядоченному множеству [1, с. 1].

Реализация алгоритма линейного поиска представлена на рисунке 1.

Рисунок 1. Реализация алгоритма линейного поиска

Давайте посмотрим на последовательность шагов алгоритма:

1. Поиск начинается с первого элемента множества.

2. Текущий элемент сравнивается с искомым элементом, если искомый элемент и значение в текущем индексе совпадают, функция возвращает текущий индекс.

3. Иначе значение индекса увеличивается и повторяется шаг 2 до тех пор, пока не будет достигнут конец множества.

Временная сложность алгоритма O(n), где n – количество элементов множества. Алгоритм линейного поиска практически редко используется, потому что другие алгоритмы поиска, такие, как алгоритм бинарного поиска и хеш-таблицы, позволяют значительно ускорить выполнения поиска. Например, для некоторого множества с n элементами лучше всего, когда значение искомого элемента равна первому элементу множества, и в этом случае требуется только одно сравнение. Худший случай - когда искомый элемент отсутствует (или встречается только один раз в конце), и в этом случае необходимы n сравнений. Другими словами, если множество содержит n элементы, наихудший сценарий для поиска элемента - это итерация. Скорость поиска линейно возрастает с количеством элементов множества. Следовательно, алгоритм линейного поиска эффективен, когда множество не содержит много элементов.

Далее рассмотрим алгоритм бинарного(двоичном) поиска. Бинарный поиск применяется к отсортированному массиву или списку. Бинарный поиск делит диапазон значений на половину и продолжает сужать поле поиска до тех пор, пока искомый элемент не будет найден. Это классический пример алгоритма «разделяй и властвуй».

Рассмотрим шаги данного алгоритма:

1. Поиск начинается с середины массива. Поскольку массив отсортирован, это говорит о том, что будет ли искомый элемент находиться в левой половине или в правой половине массива.

2. После того, как массив разделен на две части, можно исключить всю половину массива, который, как мы знаем, не содержит искомый элемент.

3. Повторяется тот же подход (начиная с середины). Это повторяется снова и снова, до тех пор, пока не будет найден искомый элемент или исключен весь набор.

Алгоритм можно реализовать рекурсивно или итерационно. На рисунке 2 показана реализация данного алгоритма, реализованный с помощью итерационного подхода.

Реализация алгоритма бинарного поиска представлена на рисунке 2.

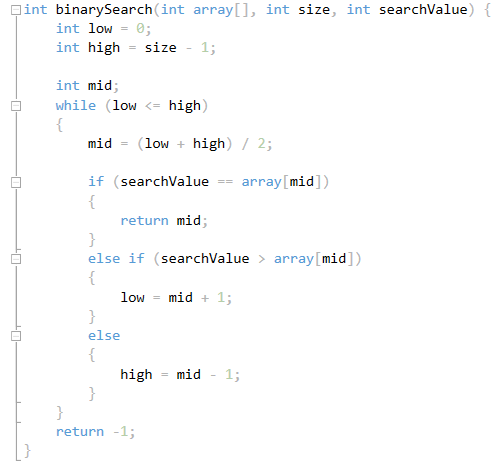
Рисунок 2. Реализация алгоритма бинарного поиска

Какое максимальное количество сравнений для этого алгоритма потребуется для проверки всего массива? Если мы начнем с массива который содержит n элементов, около  элементов останется после первого сравнения. После второго сравнения будет около   . Потом   , 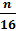  и так далее.

Когда цикл закончится, мы получаем массив, в котором есть только один элемент. Либо это искомый элемент, либо искомого элемента нет.  Количество сравнений, необходимых для достижения этой точки, равно i, где 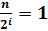. Решение для i дает нам i = 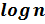. Следовательно, временная сложность данного алгоритма O 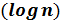, где n – количество элементов множества [2, с. 1].

В отличии от алгоритма линейного поиска, данный алгоритм относительно быстро выполняет поиск. Но этот алгоритм может применим только к сортированному массиву [1, с. 1].