ВЛИЯНИЕ ТУРБУЛЕНТНОСТИ АТМОСФЕРЫ НА ЭФФЕКТИВНОСТЬ ЛАЗЕРНЫХ ТЕЛЕКОММУНИКАЦИЙ

INFLUENCE OF ATMOSPHERIC TURBULENCE ON THE EFFICIENCY OF LASER TELECOMMUNICATIONS

Boris Kuzyakov

Candidate of Physico - Mathematical Sciences, Associate Professor, MIREA–Russian Technological University, LAS–Laser Association, Russia, Moscow

Аннотация. В статье рассматривается влияние турбулентности атмосферы на эффективность лазерных телекоммуникаций. Показано, что одним из основных параметров, характеризующих возмущения и неоднородности атмосферы, является структурная постоянная её показателя преломления. Приведены зависимости структурной постоянной от конкретного местоположения приёмо-передающей аппаратуры, от розы ветров и времени суток.

Ключевые слова: турбулентность атмосферы, базовые параметры, лазерные телекоммуникации, структурная постоянная показателя преломления, роза ветров, суточные флуктуации и изменения.

Турбулентный характер движений воздушных масс в атмосфере во многом определяет скорости образования плотности различных облаков, их высотное распределение, перенос разнообразных загрязнений, параметры процессов теплообмена и т. п.

При этом, структурная постоянная показателя преломления атмосферы С_n служит одним из основных параметров, характеризующих её возмущения и неоднородности. Знание изменений величины С_n , крайне необходимо для систем адаптивной оптики наземных телескопов и лазерных комплексов телекоммуникаций в местах их конкретного расположения. Значительные усилия многих научно-исследовательских фирм во всём мире, направлены на разработку модели С_n.

В разработке модели выделяются несколько основных этапов [1 -3]: выбор общего вида аналитической формулы; определение её основных параметров; оценка адекватности описания. В одном из вариантов, модель С_n представляют в виде суммы экспоненциальных членов [ 3, 4]:

C_n² (ξ ) = A exp{- ξ/H_A } + B exp{- ξ/H_B } + Cξ¹⁰ exp{- ξ/H_C } + D exp{- (h – H_D )²/ 2d² },                                  (1)

где, А – коэффициент для приземной турбулентности; Н_А - приземная высота; В, Н_В - то же для тропосферы; С, Н_С – определяют тропопаузу; D - отвечает за дополнительный слой толщиной d, который часто наблюдается в эксперименте.

Для Российской Федерации, весьма интересна структурная постоянная показателя преломления атмосферы, например, в Байкальском регионе. Её модель HV 10 (Хафнагеля – Волли) или HAP (Hufnagel–Andrews–Phillips ) [5, 6] была разработана в связи с установкой Большого солнечного вакуумного телескопа БАО ИСЗ СО РАН, вблизи озера Байкал, на высоте 280 м. Главная особенность модели HV 10, состоит в том, что это полуэмпирическая модель, основанная на физических предпосылках и экспериментальных данных. Обобщение модели HAP привело к следующему выражению:

C_n² (ξ ) = M [0,0059 (v/27)² (10^-5 ‧ (ξ + h_s )¹⁰ exp{- (ξ + h_s )/1000 } + 2,7 ‧ 10^-16 exp{- (ξ + h_s )/1500 }] + C_n² (ξ₀ ) ( ξ₀ / ξ )^p , (2)

где, h_s - высота над уровнем моря, C_n² (ξ₀) - усреднённое значение структурной характеристики показателя преломления на высоте ξ₀ , параметр М отвечает за среднюю фоновую приземную турбулентность на высоте ~ 1 км, параметр р определяет зависимость от времени суток. Более подробная информация по этим параметрам М и р, содержатся в работах [3, 4].

Для сопоставления разработанных моделей разными фирмами, часто используют два параметра: радиус когерентности плоской волны r₀  и угол изопланатизма атмосферы θ. Радиус когерентности плоской волны r₀, который так же называют параметром Фрида, определяется по формуле:

∞

r₀ = (0,423 k² sec α ∫₀ d ξ C_n² (ξ ))^-3/5 ,                                                                                    (3)

где k = 2π/λ.

Угол изопланатизма θ задаётся следующим выражением:

∞

θ = (2,91 k² ∫₀ d ξ ξ^5/3 C_n² (ξ ))^-3/5 ,                                                                                     (4)

Для разработанной модели БАО в летний период, авторы работы [5, 6] получили радиус когерентности r₀ = 4,6 см. Эта величина хорошо согласуется с данными из других источников [7, 8].

 Далее, для сравнения, приведены базовые параметры для ряда моделей, на длине волны 0,5 мкм, разработанных разными научными организациями (таблица 1).

Таблица 1.

Базовые параметры атмосферы для ряда рассмотренных моделей

Приведённые в таблице 1 научные организации [9 - 13], работают в разных регионах. Обсерватория Мауна Кеа расположена на вершине одноименного вулкана на острове Гавайи. Её телескопы установлены на высотах от 3790 до 4190 м. над уровнем моря в США. Обсерватория AMOS расположена на острове Мауи. Паранальская обсерватория работает на вершине горы Серро-Параналь, на высоте 2 635 м. над уровнем моря, в пустыне Атакама, Чили.

Приведенные данные в таблице 1, показывают весьма значительный разброс величин:для θ - он превышает 200 %, а диапазон вариации величины r₀ - более 300 %.

Поэтому, следует заметить, что для построения наиболее адекватной модели атмосферы, включающей величины r₀ и θ, необходимо знание реальных профилей ветра и структурной характеристики показателя преломления в месте расположения измерительной системы. Конкретные количественные данные можно использовать из доступной климатической базы данных, хранящихся в архиве NCEP / NCAR. Реанализ NCEP/NCAR — это атмосферный реанализ, созданный Национальным центром прогнозирования окружающей среды (NCEP) и Национальным центром атмосферных исследований (NCAR). Это постоянно обновляемый набор данных в виде глобальной сетки, который представляет состояние атмосферы Земли, включая наблюдения и результаты численного прогнозирования погоды (NWP) с 1948 года по настоящее время.

Кроме конкретного местоположения приёмо-передающей аппаратуры на величину С_n, весьма существенно, влияет роза ветров. Этими вопросами так же занимаются во многих странах [14]. Пример зависимости С_n от скорости ветра v приведён на рис. 1.

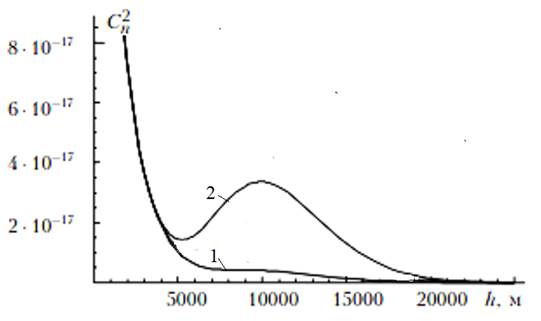
Рисунок 1. Влияние параметраv на зависимость структурной характеристики С_n: 1– v = 30 м/с ; 2 - v = 10 м/с

Наряду с этими факторами, величина С_n претерпевает изменения в течении суток [15, 16]. Суточные вариации величины С_n в летний период, в пункте наблюдения «Томск», измеренные в недавние времена, показаны на рисунке 2.

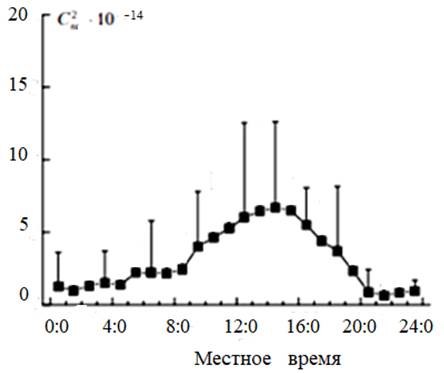
Рисунок 2. Изменение величины С_n в течение суток; тонкие вертикальные линии показывают СКО в выборочных точках измерений

Данные рисунка 2 показывают значимые изменения величины С_n в течении суточных измерений.

Таким образом, приведенные в представленной статье данные, доказывают. что при необходимости применения в анализе работы и в самой работе оптической линии связи, адекватной модели атмосферы, необходимо учитывать точное географическое местоположение модулей системы связи, с их высотой над уровнем моря, реальную розу ветров и время суток сеанса связи.