Методы ускорения деления целых чисел большой разрядности

Аннотация. В статье рассматривается методы, которые позволяют уменьшить время выполнения для алгоритма деления целых чисел большой разрядности. Интерес к данной теме основан на том, что арифметика с числами большой разрядности широко используется в системах с ассиметричным шифрованием и в алгоритмах, связанных с факторизацией больших целых чисел.

Abstract. The article considers methods that allow to reduce the execution time for the algorithm of division of integers of large digit capacity. Interest in this topic is based on the fact that arithmetic with large-digit numbers is widely used in systems with asymmetric encryption and in algorithms related to the factorization of large integers.

Ключевые слова: алгоритм деления, методы ускорения для алгоритма деления больших чисел.

Keywords: Algorithm of division, acceleration methods for the algorithm of division of large numbers.

Задача оптимизации деления целых чисел большой разрядности (далее ЦБР-числа) – одна из наиболее важных и сложных вычислительных задач длинной арифметики. В статье рассматриваются методы ускорения операции деления ЦБР-чисел на примере алгоритма деления «столбиком», который реализован с помощью операций вычитания и сдвига.

Рассмотрим классический алгоритм деления «столбиком» (a>0, b>0, a>b), который представлен Алгоритмом 1.

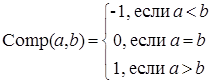
С целью повышения эффективности вычислений в данный алгоритм деления ЦБР-чисел внесем следующие изменения в структуру данных и алгоритм вычислений:

1)  «реальные» сдвиговые операции shl и shr (по основанию radix) заменяются виртуальными сдвигами;

Под термином «реальные» будем понимать преобразования, которые изменяют структуру данных ЦБР-числа. Под виртуальным сдвигом будем понимать преобразование, которое не изменяет структуру данных ЦБР-числа. В приведённом алгоритме деления имеем дело с «реальными» сдвиговыми операциями, так как изменяется структура данных ЦБР-числа – длина числа;

2)  в ходе выполнения алгоритма изменяется основание системы счисления radix.

В первом случае, для того чтобы заменить реальные операции сдвига виртуальными, достаточно в структуру данных внести следующие изменения:

·     ввести в структуру данных ЦБР-числа дополнительные поля LSB и MSB, которые хранят начальный и конечный адреса данных ЦБР-числа. Введение таких полей позволяет не только более эффективно определять количество сдвигов, которые необходимо производить при делении и других арифметических операциях с ЦБР-числами, но и эффективно производить сравнение таких чисел.

Результатом таких изменений является повышение эффективности операции деления, причем в некоторых случаях она может достигать значительных показателей. Подтверждением этого факта могут служить данные, приведенные в таблице 1. Для сравнительного анализа эффективности алгоритма 1 с реальными и виртуальными сдвигами использовались следующие данные:

·     длина делимого ЦБР-числа изменяется в диапазоне от 1000 до 1200 байтов (radix-256);

·     длина делителя ЦБР-числа – один байт.

Таблица 1.

Сравнительные характеристики алгоритма деления с реальными и виртуальными сдвигами

Соответствующие данные из таблицы 1 представлены на диаграмме рисунка 1.

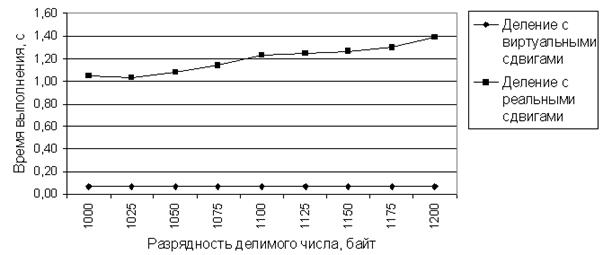
Рисунок 1. Сравнительные характеристики алгоритма деления с реальными и виртуальными сдвигами

Во втором случае можно повысить эффективность операции деления, изменяя основание системы счисления. В самом деле, анализируя текст алгоритма 1, можно отметить, что наиболее критичной характеристикой, оказывающей наибольшее влияние на эффективность алгоритма деления, являются строки 9–12. Данный фрагмент алгоритма представляет собой итеративный процесс приближения значения числа a к значению числа d. Естественно, что количество операций вычитания – это основной параметр, который влияет на эффективность всего алгоритма деления. Таким образом, задача состоит в том, чтобы уменьшить количество операций вычитания (за счет более эффективного выравнивания ЦБР-чисел по старшим разрядам) и, как результат, повысить эффективность операции деления ЦБР-чисел. Поясним данный метод на следующем примере.

Пусть минимальным элементом хранения данных в числах a и b будет блок в 8 бит. Тогда системой счисления для ЦБР-числа будет 256-ричная система счисления (radix-256=2⁸). Пусть длина делимого ЦБР-числа (число a) составляет два байта, длина делителя (число b) – один байт (в соответствии с рисунком 2). Тогда в процессе деления числа a на число b будет выполнено 255 вычитаний для каждого из блоков, а всего – 510 вычитаний.

Рисунок 2. Распределение данных для чисел a и b, (radix-256=2⁸)

Теперь изменим систему счисления и определим блок хранения данных в 4 бита. В этом случае системой счисления для ЦБР-числа будет 16-ричная система счисления (radix-16=2⁴). Тогда при тех же исходных данных получим, что в процессе деления числа a на число b будет выполнены 15 операций вычитания для каждого из блоков (рисунок 3), а всего – 60 вычитаний.

Рисунок 3. Распределение данных для чисел a и b, (radix-16=2⁴)

Очевидно, что при указанных выше исходных данных для чисел a и b для различных систем счисления получим следующую сводную таблицу (таблица 2):

Таблица 2.

Количество вычитаний при операции деления в различных системах счисления

Таким образом, для того чтобы повысить производительность операции деления «столбиком», достаточно массив данных представить в системе счисления с меньшим основанием (в отличие от операции умножения).

В процессе вычислений переход к другой системе счисления можно осуществить различными способами:

способ 1 – осуществлять преобразования и вычисления на «месте» в пределах обрабатываемого блока данных;

способ 2 – предварительно преобразовать весь массив данных ЦБР-числа в массив данных с системой счисления с меньшим основанием, выполнить вычисления, а затем произвести обратное преобразование. В данной публикации рассматривается именно второй способ реализации.

Сущность метода, при котором осуществляется преобразование массива данных из системы счисления radix-256=2⁸ в системы счисления radix-16=2⁴ и radix-4=2², можно продемонстрировать с помощью рисунка 3 (при этом минимальным элементом хранения данных в массиве является по-прежнему один байт).

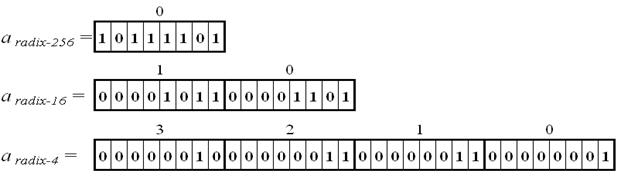
Рисунок 3. Преобразование данных из radix-256 в radix-16 и radix-4

Выбор второго варианта реализации обусловлен следующими причинами:

1)  высокой скоростью преобразования;

2)  минимальными изменениями в алгоритме деления ЦБР-чисел.

Следует, однако, отметить, что при данном способе преобразования и вычислений следует учитывать тот факт, что наименьшее основание системы счисления ещё не гарантирует наибольший прирост скорости выполнения алгоритма. В самом деле, пусть сложность алгоритма деления для системы счисления по основанию radix-2 составляет Q(mn) [1], где m, m+n – количество элементов в делителе и делимом ЦБР-числах соответственно. Тогда при переходе к системе счисления по основанию radix-4 следует ожидать, что сложность алгоритма деления составит k´Q(m’n’), где коэффициент k=31,875/21,250=1,5 (таблица 2), m’=m/2, n’=n/2. В результате получим k/4´Q(mn) = 0,375´Q(mn) в системе счисления по основанию radix-4. В реальности сложность алгоритма деления составила в среднем 0,8´Q(mn) в системе счисления по основанию radix-4 по отношению к системе счисления по основанию radix-2. Данные оценки получены по результатам тестирования (данные таблиц 3, 4 и соответствующие им диаграммы на рисунках 4 и 5).

В таблице 3 представлены следующие данные:

·     длина делимого ЦБР-числа изменяется в диапазоне от 1000 до 7000 байтов (radix-256);

·     длина делителя ЦБР-числа составляет 100 байтов.

Таблица 3.

Сравнительные характеристики алгоритма деления в различных системах счисления при возрастании размерности делимого ЦБР-числа

Соответствующая диаграмма представлена на рисунке 4.

Рисунок 4. Сравнительные характеристики алгоритма деления в различных системах счисления при возрастании размерности делимого ЦБР-числа

В таблице 4 представлены следующие данные:

·     длина делителя ЦБР-числа изменяется в диапазоне от 100 до 800 байтов (radix-256);

·     длина делимого ЦБР-числа составляет 1000 байтов.

Таблица 4.

Сравнительные характеристики алгоритма деления в различных системах счисления при возрастании размерности делителя ЦБР-числа

Соответствующая диаграмма представлена на рисунке 5.

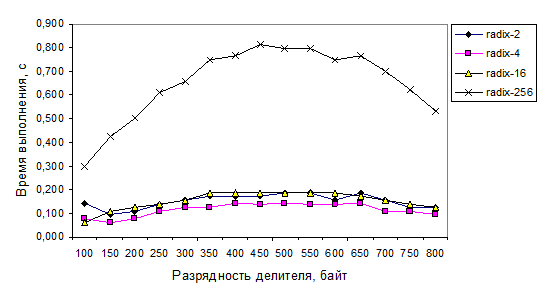
Рисунок 5. Сравнительные характеристики алгоритма деления в различных системах счисления при возрастании размерности делителя ЦБР-числа

Результаты:

По результатам тестирования были получены следующие результаты:

· возможность ускорения последовательного алгоритма деления «столбиком» для ЦБР-чисел за счет использования механизма виртуальных сдвигов и использования различных систем счисления;

· коэффициент ускорения k находится в диапазоне 4£k£6 для различных систем счисления.

Выводы:

Анализируя полученные результаты можно сделать следующие выводы:

· для получения ускорения алгоритма деления «столбиком» достаточно перейти к системе счисления с меньшим основанием radix-X;

· оптимальным выбором системы счисления, при которой наблюдается наибольший коэффициент ускорения, является 4-ричная (radix-4) система счисления.