Оценка эффективности использования фильтров гармоник в среде Matlab

Evaluation of the efficiency of using harmonic filters in the Matlab environment

Alexey Yudin

doctor of technical science, Head of Department of Electrical Engineering and Industrial Electronics FGBOU VO «P. A. Solovyov Rybinsk State Aviation Technical University», Russian Federation, Rybinsk

Аннотация. Для обеспечения требований по электромагнитной совместимости часто применяют пассивные фильтры гармоник. Для анализа эффективности их применения необходимо проведение моделирования процессов, протекающих в энергосистеме с установленным фильтром. В статье рассматривается реализация проверочного расчета в среде Matlab. В качестве источника высших гармоник рассмотрен тиристорный регулятор переменного напряжения.

Abstract. Passive harmonics filters are often used to ensure the requirements for electromagnetic compatibility. To analyze the effectiveness of their application, it is necessary to simulate the processes taking place in the power system with the filter installed. The article deals with the implementation of the verification calculation in the Matlab environment. The thyristor regulator of alternating voltage is considered as a source of higher harmonics.

Ключевые слова: электромагнитная совместимость; пассивный фильтр гармоник; высшие гармоники; моделирование; Matlab.

Keywords: electromagnetic compatibility; passive harmonic filter; higher harmonics; modeling; Matlab.

Каждый электроприемник рассчитан для работы при определённых параметрах электрической энергии, поэтому для его нормальной работы должно быть обеспечено требуемое качество. Необходимость проектирования и установки фильтров гармоник возникает из-за плохого качества электроэнергии, а также из-за ограничений поставщика электроэнергии, которые нормируются регулирующими организациями, такими как IEEE и МЭК. Наиболее доступным методом снижения гармонических искажений напряжения и тока является применение пассивных фильтров. В настоящее время многие сети содержат по нескольку источников гармоник, которые создают неприемлемый уровень искажений в точке подключения к энергосистеме и которые могут нанести ущерб другим потребителям. Имеется необходимость оценки эффективности работы фильтров. Для проведения такой оценки  требуется разработка специальных моделей.

Нормы качества электрической энергии в системах электроснабжения общего назначения регламентируются ГОСТ 32144-2013 [1]. Несинусоидальность напряжения (тока) оценивается коэффициентом гармонических составляющих до 40-го порядка КU(n)i в процентах от  основной гармонической составляющей.

Анализ работы фильтра гармоник проведем в три этапа. На первом этапе определяем спектральный состав напряжения. Для этого воспользуемся аппаратом анализа спектра (разложение в ряд Фурье). Ряд Фурье – бесконечная сумма гармонических составляющих: постоянной составляющей  основной гармоники с частотой  и высших гармонических составляющих, частоты которых кратны основной частоте. Каждая гармоника характеризуется амплитудой , начальной фазой  и частотой , где k = 1, 2, 3, … – порядковый номер гармоники. Разложение в ряд Фурье может быть выполнено аналитически, решением интеграла Фурье или с помощью алгоритма быстрого преобразование Фурье (БПФ).

Для выполнения БПФ в MATLAB используется функция fft. Выполнение команды вида Y = fft(X) вычисляет для массива данных X дискретное преобразование Фурье, используя FFT-алгоритм быстрого Фурье-преобразования.

Для перехода к спектру в общепринятом смысле отбрасывают правую половину спектрограммы, а амплитуды в левой части умножают на 2 за исключением первого элемента, который не имеет зеркального отражения и представляет собой величину постоянной составляющей. Кроме того, нормируют все амплитуды гармоник, разделив их на число выборок сигнала [2].

Для примера рассмотрим форму напряжения, соответствующую работе тиристорного регулятора с фазовым управлением с заданным моментом коммутации тиристора. Для этого используется пользовательский скрипт vvrreg.m в среде Matlab, который осуществляет генерирование опорной синусоиды и ее модуляцию прямоугольным импульсом, время завершения которого соответствует полупериоду сетевого напряжения, а начало – моменту фазовой коммутации при тиристорном регулировании.

Результатом работы данного скрипта являются графики, отображающие форму сигнала и его спектр. Форма и спектр напряжения для момента коммутации 5 мс приведена на рисунке 1. Для дальнейшего анализа требуется определить амплитуду первой А1 и третьей А3 в спектре сигнала, которые изображены на рисунке 1. Амплитуда первой гармоники определяется по нижнему графику рисунка 1 по значению частоты на оси абсцисс равному 50 Гц, а третьей гармоники соответственно на частоте 150 Гц. Впоследствии эти значения используются в качестве исходных значений источника ЭДС в схеме замещения сети с установленным фильтром. То есть, проводиться анализ прохождения каждой гармоники в спектре через частотно зависимую цепь, какой является фильтр гармоник совместно с элементами энергосети. При этом нужно учитывать, что сеть имеет кроме активного также и индуктивное сопротивление.

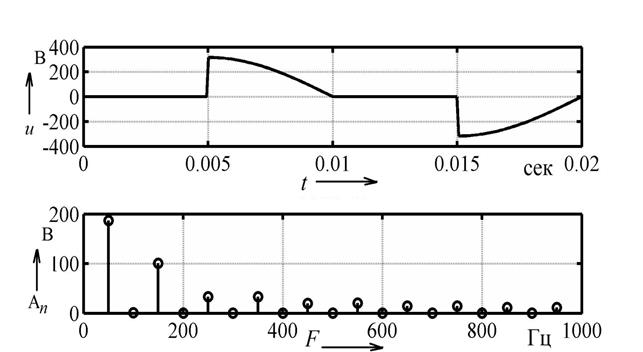
Рисунок 1. Форма и спектр напряжения для момента коммутации 5 мс

На втором этапе производится необходимое построение модели сети с установленным фильтром, схема которой изображена на рисунке 2. Здесь пассивный фильтр содержит индуктивность, емкость и активное сопротивление и подключен параллельно нагрузке Z_S

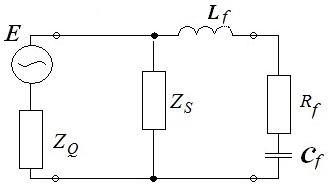
Рисунок 2. Схема сети с  фильтром

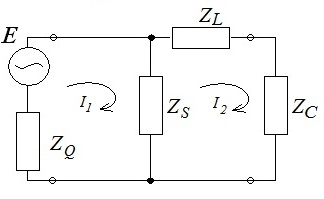
Рисунок 3. Схема замещения сети с фильтром

Схема замещения, изображенная на рисунке 3, при использовании метода контурных токов может быть описана системой уравнений:

Для решения этой системы в среде Matlab его можно представить в матричной форме

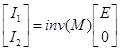, где .

Комплексные сопротивления, входящие в состав матрицы M: – сопротивление источника, – сопротивление нагрузки, – индуктивное сопротивление  фильтра (дроссель), – емкостное сопротивление фильтра (конденсатор), F– частота, на которой производится расчет. Зная контурные токи можно найти ток, протекающий через нагрузку IS (как разность  между первым и вторым контурными токами).

На третьем этапе производится расчет тока в нагрузке на частоте первой In1 и  третьей In3 гармоники, используя модель, полученную на втором этапе при разных значениях индуктивности. Кроме того, рассчитывается  коэффициент гармонической составляющей для третьей гармоники: Kn3= In3/ In1.

Пример расчета коэффициент гармонической составляющей для третьей гармоники представлен на рисунке 4.

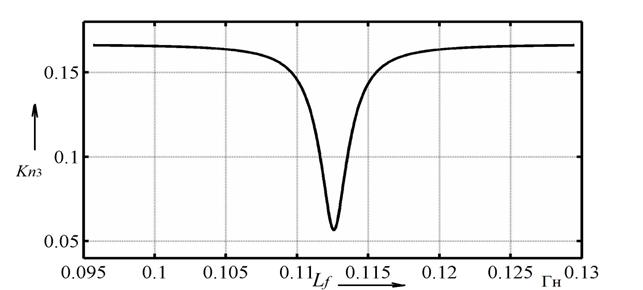
Рисунок 4. Коэффициент гармонической составляющей Kn3

Приведенные результаты анализа работы фильтра гармоник позволяют оценить эффективность его применения в условиях заданной электромагнитной обстановки.

Как видно из рисунка 4 коэффициент  гармонической составляющей для третьей гармоники снизился с 17 % до 5 %. При этом следует стремиться не уменьшать In1 так как это приводит к дополнительным потерям. Дополнительно анализ позволяет оценить влияния индуктивности фильтра, то есть сформулировать требования к погрешности изготовления дросселя фильтра.