Комплексный подход к преподаванию математики при дистанционном обучении детей с ограниченными возможностями здоровья
Конференция: VI Международная заочная научно-практическая конференция «Научный форум: педагогика и психология»
Секция: Коррекционная педагогика

VI Международная заочная научно-практическая конференция «Научный форум: педагогика и психология»
Комплексный подход к преподаванию математики при дистанционном обучении детей с ограниченными возможностями здоровья
An integrated approach to the teaching of mathematics with distance learning children with disabilities
Indira Hadzharova
candidate of pedagogical sciences, From state special educational institution "the Republican centre of remote education of children – disabled", MBOU "Gymnasium № 11", Russia, Dagestan, Makhachkala
Patimat Magomedova
Student, Dagestan state University, Russia, Dagestan, Makhachkala
Аннотация: В статье речь идет о комплексном подходе к раскрытию содержания математических понятий при дистанционном обучении детей - инвалидов. Работа посвящена совершенствованию такой работы на уроках математики.
Abstract: In this article we are talking about an integrated approach to the disclosure of the content of mathematical concepts in distance education of children with disabilities. The work is devoted to improvement of such work in mathematics lessons.
Ключевые слова: обучение математике; комплексный подход; дети с ограниченными возможностями здоровья.
Keywords: learning math; an integrated approach; children with disabilities.
Одним из важнейших прав и свобод граждан в современном обществе является право каждого на образование, которое гарантируется основными нормативным актами государства. В рамках программы реализации приоритетного национального проекта «Образование» на 2009 - 2012 годы в республике Дагестан идет реализация мероприятий по созданию условий для организации дистанционного обучения детей - инвалидов. Постановлением Правительства Республики Дагестан от 16.10.2009 года № 360 был создан Государственное казенное образовательное учреждение Республики Дагестан «Республиканский центр дистанционного обучения детей - инвалидов».
Обучение с использованием дистанционных образовательных технологий значительно расширяет возможности детей с особыми образовательными потребностями, позволяет во многих случаях обеспечить освоение основной общеобразовательной программы в полном объёме.
При дистанционной организации учебного процесса детей с ограниченными возможностями очень важно использовать комплексный подход к обучению, как фактор формирования системности знаний учащихся.
В работе с проблемными детьми наглядные методы наиболее доступны и важны, особенно на начальных этапах работы. При их применении следует помнить такие особенности детей, как замедленный темп восприятия, сужение объема восприятия, нарушение точности восприятия. Иллюстрации должны быть крупными, доступными, в реалистическом стиле. [1, с.112]
Дети с отклонениями в развитии испытывают трудности в восприятии и переработке вербальной информации, у большинства из них страдает речевое развитие, поэтому словесные методы следует сочетать с применением наглядных и практических.
Предпочтение поэтому отдается методам, помогающим наиболее полно передавать, воспринимать, удерживать и перерабатывать учебную информацию в доступном для обучающихся виде, опираясь на сохранные анализаторы, функции, системы организма. [7, с. 56]
Задача каждого учителя – сделать жизнь наших детей-инвалидов радостной и счастливой. В этих условиях центру нужен учитель, способный подойти комплексно к обучению и воспитанию детей с проблемами здоровья.
Главная задача учителя при работе с инвалидами состоит в том, чтобы организовать учебный процесс так, чтобы каждый ученик осознал свою значимость, свою принадлежность к обществу, развивать познавательный интерес, давать возможность принимать участие в научных экспериментах и исследованиях, чтобы учащиеся получили системные знания по изучаемым наукам.
Часто обнаруживается в практике обучения математике отсутствие системности в знаниях учащихся. Для устранения этих пробелов в знаниях учащихся, в частности, при работе с детьми с ограниченными возможностями здоровья, необходимо придерживаться пути перехода от актуального уровня знаний к ближайшему уровню. Суть такой методики рассмотрим на конкретных, более популярных примерах из практики обучения математике в общеобразовательной школе.
В основе вычислений площадей фигур на плоскости лежат знания о вычислениях площадей прямоугольника и треугольника. С вычислением площади прямоугольника учащиеся знакомятся уже в начальной школе, накладывая на фигуру единицу измерения площади (квадраты разных размеров), после чего обобщается такой подход вычислением результата таких действий путем умножения длины и ширины прямоугольника. Знакомство учащихся с различными треугольниками по их углам (прямоугольный, остроугольный и тупоугольный) дает возможность для перехода к ближайшему уровню знаний, к вычислению площади прямоугольного треугольника, разбивая данный прямоугольник его диагональю на два равных прямоугольных треугольника. Обобщая такое осознание, мы приходим к выводу о том, что площадь прямоугольного треугольника равна произведению длин его катетов (сторон, образующих прямой угол), разделенному на 2, то есть 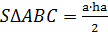 , где а и b – длины катетов прямоугольного треугольника, впоследствии один из катетов «становится» высотой прямоугольного треугольника. Далее, любой треугольник представляется или двумя прямоугольными треугольниками с одной и той же высотой DC (рис. 1а), или же прямоугольником, состоящим из двух таких треугольников, или же заменой треугольника одним прямоугольником, ширина которого в два раза короче высоты данного треугольника (рис.1б)
, где а и b – длины катетов прямоугольного треугольника, впоследствии один из катетов «становится» высотой прямоугольного треугольника. Далее, любой треугольник представляется или двумя прямоугольными треугольниками с одной и той же высотой DC (рис. 1а), или же прямоугольником, состоящим из двух таких треугольников, или же заменой треугольника одним прямоугольником, ширина которого в два раза короче высоты данного треугольника (рис.1б)

Рисунок 1. Представление треугольника двумя прямоугольными треугольниками
На этом этапе решается и обратная задача (переходя от актуального уровня к ближайшему): приводя вычисление площади любого треугольника к вычислению площади прямоугольника. При этом учащиеся не отходят от истины в том, что площадь любого треугольника равна половине произведения длины одной из его сторон на длину его высоты на эту сторону:
 .
.
Цепочка перехода от актуального уровня знаний к ближайшему уровню не обрывается, а продолжается и на следующих этапах обучения: от имеющейся формулы вычисления площади треугольника переходят к другим формулам по схеме:
 (1)
(1)
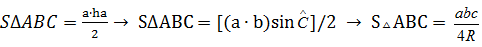 ; (2)
; (2)
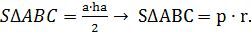 (3)
(3)
Вычисление площади треугольника различными вариантами усваивается учащимися с доказательными рассуждениями, и этот материал запоминается ими, становится базовым фондом их математических знаний и умений пользоваться ими в практике.
Чтобы материал стал доступным при дистанционном обучении, учитель должен найти разные подходы к обучению в зависимости от состояния ученика: отправить презентацию, видео-урок, попробовать организовать так, чтобы ученик сам выполнил какую - то модель геометрической фигуры и т.д.


