Применение технологии развития критического мышления в процессе обучения геометрии в 10 классе

Аннотация. в данной статье рассматриваются особенности технологии развития критического мышления, способствующие повышению качества знаний учащихся. В качестве примера приведен урок геометрии по теме «Призма».

Ключевые слова: критическое мышление; технология крити­ческого мышления; приемы ТРКМ; призма; прием «Верные и неверные утверждения»; прием «Инсерт».

На сегодняшний этап развития образования необходимо начать использовать образовательные технологии, которые реализуют совре­менные требования федерального стандарта. И одной из технологий, способствующий раскрытию способностей каждого ученика и воспи­тание его как личности, является технология развития критического мышления.

Как утверждает американский ученый Д. Халперн, критическое мышление – это применение таких когнитивных навыков и приемов, которые увеличивают вероятность получения желаемого результата [5, с. 49].

С.И. Заир-Бек считает, что критическое мышление (как это понимается в технологии РКМЧП) – это процесс соотнесения внешней информации с имеющимися у человека знаниями, выработка решений о том, что можно принять, что необходимо дополнить, а что – отвергнуть. Критическое мышление учит активно действовать и помогает понять, как надо поступать в соответствии с полученной информацией. Главная цель технологии развития критического мышления – развитие интеллектуальных способностей ученика, позволяющих ему учиться самостоятельно [3, с. 5].

Для развития критического мышления необходимо создание и применение специальных методических инструментов, одним из которых, является разработанная американскими педагогами Дж. Стил, К. Мередитом и Ч. Темплом педагогическая технология развития критического мышления посредством чтения и письма [4, с. 12].

Учебное занятие по этой технологии состоит из трех фаз (стадий): «Вызов» – «Осмысление содержания» – «Рефлексия».

Первая стадия – «Вызов» – побуждения имеющихся знаний и интересов к получению новой информации, постановка учеником собственных целей обучения.

Вторая стадия – «Осмысление содержания» – получение новой информации, корректировка учеником поставленных целей обучения.

Третья стадия – «Рефлексия» – размышление, рождение нового знания, постановка учеником новых целей обучения [3, с. 13].

Существует много приёмов и стратегий технологии критического мышления, которые можно применить на уроках математики, например: составление списка известной информации; систематизация материала (графическая): кластеры, таблицы; верные и неверные утверждения; инсерт; «плюс – минус – интересно» и т. д.

Рассмотрим урок по теме «Призма» с использованием технологии развития критического мышления.

На первом этапе урока мотивирую детей к предполагаемой деятельности. У учащихся на каждом столе находится модель призмы (на каждом столе своя модель: прямая, наклонная, правильная), чтоб познакомились как выглядят призмы.

На стадии вызова, использован прием «Верные и неверные утверждения». Организую работу по выполнению таблицы «верных-неверных утверждений». В таблице, каждое предложение начинается со слов «веришь ли ты…», и задача учащихся, определить где верные, а где неверные утверждения, и поставить в столбике «А» (+) или (-).

Таблица 1.

«Верных-неверных утверждений»

Далее, предлагаю поделиться своим мнением с классом. Заслушав ответы учащихся, заполняем первый столбец таблицы на доске (столбец А).

Таблица 2.

Заполнение столбца А

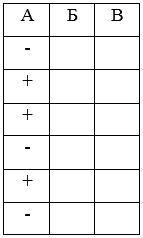
И с помощью наводящих вопросов, учащиеся определяют, что им необходимо узнать о призмах из учебника.

На стадии осмысления, учащиеся приступают к работе над параграфом, предлагаю прием «Инсерт» - знаком «V» отметить то, что они уже знали, отмечают карандашом в учебниках, то что знают. Знаком «!» отметить тот материал, который оказался новым, и знак «?» - тот материал, который не понятен после прочтения текста и затем, по окончании работы, возвращаются к вопросам, рассмотренным в начале урока и заполняют столбец «Б».

И далее, заслушав ответы учащихся, заполняем второй столбец таблицы начерченной на доске (столбец Б).

Таблица 3.

Заполнение столбца Б

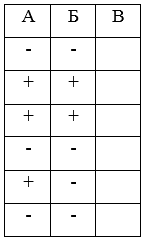
Затем прошу учащихся вернуться к тексту учебника и проанализировать, что нового узнали (!), какой материал был не понятен после прочтения текста (?). По ходу обсуждения составляют и записывают конспект.

На стадии рефлексии, организую работу над решением задач для первичного закрепления. Затем, самостоятельную работу с после­дующей самопроверкой по эталону.

И в конце урока, обсуждаем полученные результаты и окончательно заполняется таблица (столбец В).

Таблица 4.

Полученные результаты, столбец В

Таким образом, примерно так выглядят уроки геометрии с применением технологии развития критического мышления, где используются разные приемы данной технологии.