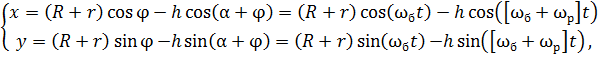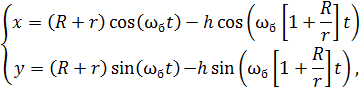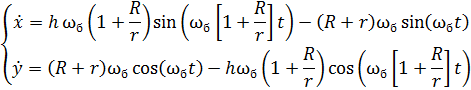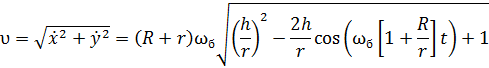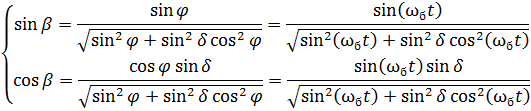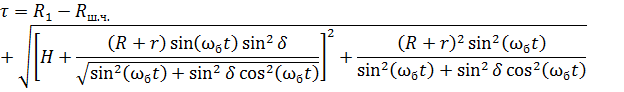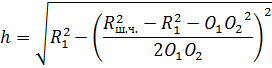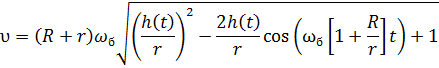ОПРЕДЕЛЕНИЕ ОСНОВНЫХ КИНЕМАТИЧЕСКИХ ПАРАМЕТРОВ ПРИ ШЛИФОВАНИИ СФЕРИЧЕСКИХ ТОРЦОВ КОНИЧЕСКИХ РОЛИКОВ

Одним из важнейших достоинств конических радиально-упорных подшипников является высокая грузоподъемность как в радиальном, так и в осевом направлениях. Исследованиями [1, 2, 3] установлено преимущество сопряжения сферической формы торца роликоопоры и борта внутреннего кольца подшипника из-за максимально возможной площади контакта, вызывающей наименьшее удельное давление в пятне контакта ролика с бортом и, как следствие, снижение потерь на трение. Кроме того, сферический торец ролика более технологичен в сравнении с другими.

Полное устранение скольжения между торцом ролика и опорным бортом не представляется возможным, поэтому актуальной остается задача его снижения. Решению этой задачи призвана качественная обработка торцевой поверхности ролика шлифованием.

Шлифование является одним из ключевых этапов обработки поверхности роликов, обеспечивающих высокую точность геометрической формы и качество поверхности, влияющих на надежность и долговечность изделия. Рассмотрим влияние кинематических параметров процесса шлифования – угловую скорость заготовки, скорость подачи и относительное перемещение инструмента – на формирование геометрии поверхности торца ролика. Комплексному анализу этих параметров в контексте торцевого шлифования конических поверхностей в исследованиях уделено недостаточно внимания.

Целью статьи является определение зависимости полной скорости вращения роликов при полном цикле обработки, припуска на операцию шлифования от времени обработки, кинематическое исследование конических роликов в процессе шлифования, позволяющие определить рациональные режимы резания для обеспечения их качественных торцовых поверхностей.

В процессе обработки торца бесцентровым шлифованием ролик совершает сложное движение: вращение вокруг своей оси и вращение вокруг оси барабана (рисунок 1)

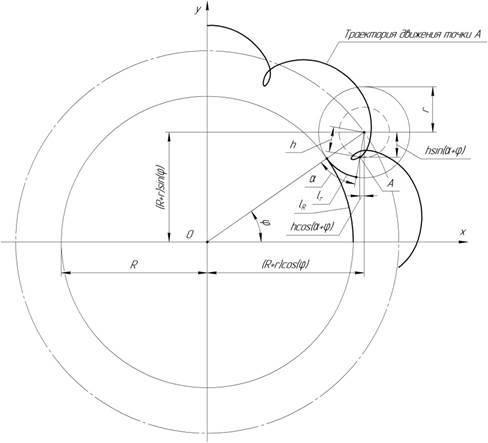
Рисунок 1. Схема движения ролика

Рассмотрим движение точки A, удаленной от центра ролика на некоторое расстояние h.

Известно, что , .

Введем оси x и y, проходящие через центр барабана. Тогда координаты точки A будут равны

Учитывая, что , получим следующее

где R – радиус барабана, r – радиус образующей сферы ролика,  – угловая скорость барабана,  – угловая скорость ролика, t – время

Продифференцировав уравнения движения ролика по времени, получим скорости по координатам x и y соответственно

Тогда модуль скорости, он же касательный вектор к траектории точки A будет равен

Рассмотрим, как ролик взаимодействует с шлифовальным кругом. Шлифовальный круг расположен под некоторым углом δ к плоскости барабана, ролик в процессе резания совершает сложное движение в плоскости круга, двигаясь по эллипсу, постепенно увеличивая сектор обработки (рисунок 2)

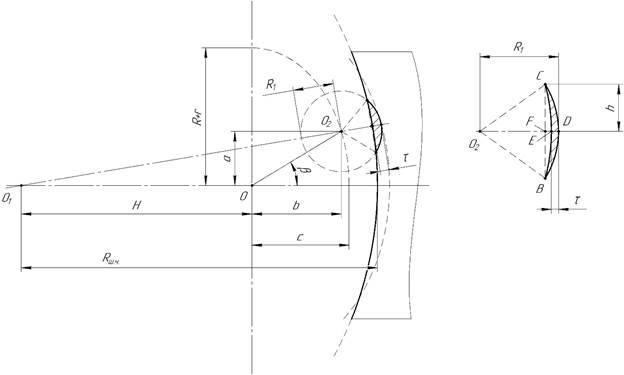
Рисунок 2. Схема движения ролика в плоскости шлифовального круга

Найдем величину съёма материала τ в зависимости от поворота барабана, принимаем, что величина вылета шлифовального круга H относительно барабана, и его угол поворота δ фиксированы.

Составим систему уравнений (рисунок 2)

Решая систему, находим искомую величину τ

где  – радиус необработанной сферы,  – радиус шлифовальной чашечки круга.

 можно найти как

где H – величина вылета шлифовального круга, b, а – координаты центра необработанной сферы на оси эллипса, которые равны

где c – длина полуоси эллипса, равная

где δ – угол поворота шлифовального круга вокруг оси барабана.

С учетом этого находим 

где углы sinβ и cos β можно найти как:

С учетом этого получаем величину съёма τ

Подставляя в полученную формулу исходные данные, получаем, что для съёма в 1,4 мм на радиусе необработанной сферы потребуется 1,82 с. (рисунок 3)

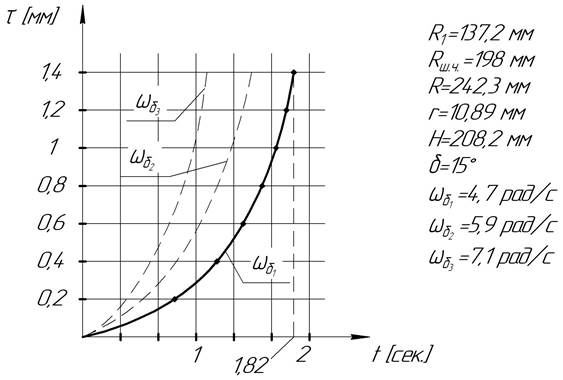
Рисунок 3. Зависимость величины съёма материала от времени

Исходя из графика видно, что чем выше угловая скорость барабана, тем быстрее происходит обработка ролика, так же съем материала растет по сложному тригонометрическому закону, в первую секунду обработки ролик только «врезается» в шлифовальный круг, и по мере прохождения сектора обработки, радиус сферы на торце ролика увеличивается. Нелинейно возрастают силы резания и скорости точек обрабатываемой сферы.

С другой стороны, величина h – переменная, которая зависит от того, на какую величину сместился ролик в процессе резания (рисунок 4)

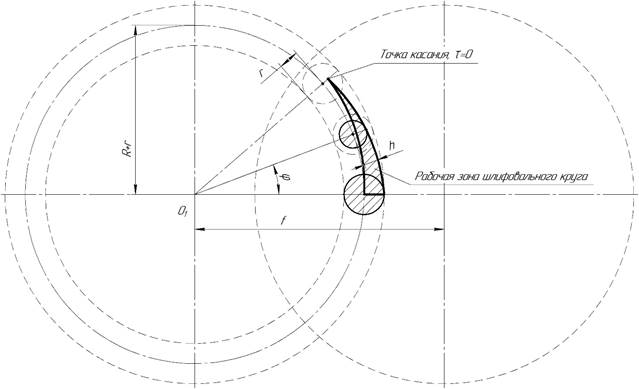
Рисунок 4. Рабочая зона шлифовального круга в процессе обработки сферы на торце конического ролика

Величину h можно найти, решив систему уравнений (рисунок 2)

где  – найдено выше.

С учетом этого, абсолютная скорость точки на торце ролика будет определятся как

Подставляя исходные данные, получаем график зависимости скорости точки на торце конического ролика от времени (рисунок 5)

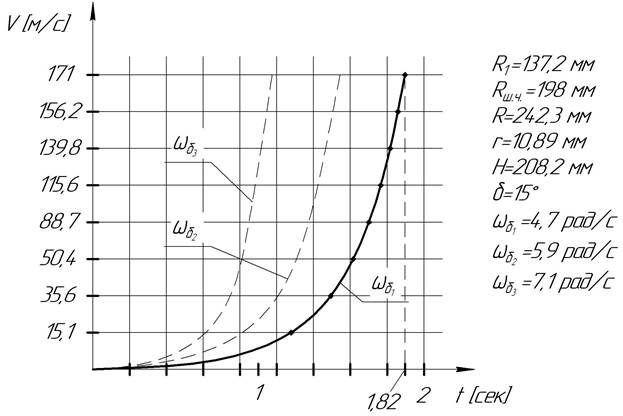
Рисунок 5. График зависимости скорости точки на торце конического ролика от времени

Из графика видно, что чем выше угловая скорость барабана, тем за меньшее время в процессе обработки угловая скорость ролика возрастет. При этом в самый последний момент, когда ролик выйдет из зоны обработки, скорость точки на краю его обработанной поверхности составит 171 м/с. Данная зависимость носит сложный тригонометрический закон и представлена в упрощенном виде.