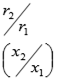ЭНТРОПИЙНЫЕ КОНФОРМАЦИИ В ТЕХНИЧЕСКИХ СИСТЕМАХ И В КОСМОЛОГИИ

ENTROPY CONFORMATIONS IN TECHNICAL SYSTEMS AND IN COSMOLOGY

Grigory Korablev

Doctor of Chemical Sciences, Professor of the Department of Physics, Udmurt State Agrarian University, Russia, Izhevsk

Аннотация. Геометрически-геодезический угол (φ = 54.733°) определяется как отношение двух составляющих: негэнтропийной  (линейное ускорение, ) и энтропийной  (центростремительное ускорение ), где tg φ =

Показано, что переход  соответствует смене вращательного движения на поступательное с поглощением энергии. И возможен обратный переход  от поступательного движения к вращательному.

На примерах армирования композитных материалов, фотонных двигателей и космологических данных продемонстрирована универсальность угла φ в системах с доминированием энтропийных переходов.

Установлена прямая математическая связь tg φ с постоянными коэффициентами в космологических параметрах Хаббла.

Динамика энтропийных взаимодействий определяет конформационные процессы рождения и развития Вселенной.

Abstract. The geometric-geodetic angle (φ = 54.733°) is defined as the ratio of two components: the negentropic  (linear acceleration, ) and the entropic  (centripetal acceleration ), where tg φ =.

It is shown that the transition   corresponds to a shift from rotational motion to translational motion with energy absorption. A reverse transition  from translational to rotational motion is also possible.

Using examples from the reinforcement of composite materials, photon engines, and cosmological data, the universality of the angle φ in systems dominated by entropic transitions is demonstrated.

A direct mathematical relationship is established between tg φ and constants in the cosmological Hubble parameters.

The dynamics of entropic interactions determine the conformational processes of the birth and evolution of the Universe.

Ключевые слова: Геодезический угол, энтропия, негэнтропия, квантовые двигатели, композитные материалы, космологические системы

Keywords: Geodesic angle, entropy, negentropy, quantum engines, composite materials, cosmological systems

Введение

Вращательное движение, как фундаментальная форма стабильности систем, описывается кинематическими параметрами [1,2], среди которых ключевую роль играет геодезический угол (φ). Его практическое применение охватывает технологии армирования аэрокосмических конструкций [3,4] и биологические процессы (намотка шелкопрядом нити) [4,5].

По этой методике цилиндрическая оболочка корпуса армируется по геодезической линии.

«Геодезическая линия - кривая определенного типа, обобщение понятия - прямая для искривленных пространств» [1,3].

На круговом цилиндре – это винтовые линии, которые дают кратчайшее расстояние между точками на поверхности вращения.

Если намотка полимерных нитей на основу аппарата идет по геодезической линии, то угол между осью вращения и вектором намотки называется геодезическим углом, который равен 54°44´=54,733° [4, 5].

Цель работы – установить универсальность φ через анализ корпускулярно-волновых взаимодействий в открытых системах. В основу положена гипотеза: геодезический угол определяет баланс энтропийных и негэнтропийных процессов при переходе между режимами движения.

Известно, что понятие энтропии, вытекающее из второго закона термодинамики, является критерием направленности процесса, и степенью неупорядоченности систем. Поэтому, в данном исследовании делается попытка объяснения вышеуказанных проблем с позиции представлений о градиенте направленности физико-химических процессов при изменении их энтропийных составляющих.

1. Исходные принципы [6]

Анализ характера изменения величины потенциальной энергии  по ее знаку для различных потенциальных полей (табл. 1) позволил установить, что значения – и соответственно  (положительная работа) соответствуют взаимодействиям, происходящим по градиенту потенциала, а + и  (отрицательная работа) имеют место при взаимодействиях против градиента потенциала.

Таблица 1.

Направленность процессов взаимодействий

Поэтому, на основе анализа первого начала термодинамики было установлено [6]:

1. В системах, в которых взаимодействие идет по градиенту потенциала (положительная работа) результирующая потенциальная энергия, как и приведенная масса, находятся по принципу сложения обратных значений соответствующих величин подсистем. Это – корпускулярный процесс, теоретической концепцией которого может являться энтропия.

2. В системах, в которых взаимодействие идет против градиента потенциала (отрицательная работа) выполняется алгебраическое сложение их масс и также соответствующих энергий подсистем. Это – волновой процесс, теоретической концепцией которого может являться негэнтропия.

3. Резонансное стационарное состояние систем выполняется при условии равенства энтропийных составляющих взаимодействий. В термодинамике открытых систем продукция энтропии в стационарном состоянии полностью компенсируется потоком негэнтропии.

4. Все явления и процессы в природе и в Мире, включая человека, технику, экономику и экологию, идут только в двух энергетических направлениях. Или - по градиенту силового поля, с минимальной затратой энергии, или - против градиента, с максимальной затратой энергии. Первое направление соответствует понятию энтропия, а второе - понятию негэнтропия (отрицательная энтропия). В динамике процессов оба явления взаимосвязаны, и дополняют друг друга.

2. Энтропийные номограммы

Гейзенберг и Дирак [7] для оценки степени структурных взаимодействий предложили обменный гамильтониан, выведенный в предположении о прямом перекрывании волновых функций взаимодействующих центров:

где:  – спиновый оператор изотропного обменного взаимодействия для пары атомов, – постоянная обмена, и – интегралы перекрывания волновых функций.

Интегралы перекрывания волновых функций моделируются [6] через величину относительной разности энергетических параметров взаимодействующих центров – коэффициент  (в %). Такой параметр является прямой характеристикой степени энтропийного равновесия в системе.

Для построения номограммы (Рис. 1) использованы:

- Данные рентгеновской дифракции (Rigaku SmartLab, λ = 1.5406 Å) для анализа фазовых переходов.

- Молекулярная динамика (LAMMPS, силовое поле CHARMM) для моделирования структурных взаимодействий.

Этот вид номограммы и ее зеркально-симметричный вариант (рисунок не приводится) позволяют оценить степень и направление структурных взаимодействий процессов фазообразования, изоморфизма и растворимости в многочисленных системах, в том числе в молекулярных [8].

В рисунке 1 увеличение значений α характеризует нарастание корпускулярных и электростатических свойств в микросистемах (энтропийная кривая). Таким образом, понятие энтропии количественно моделируется через коэффициент α, а негэтропия через величину 1/ α.

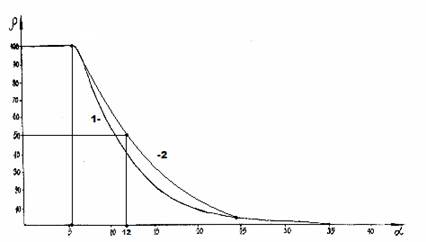
Рисунок 1. Номограмма зависимости степени структурных взаимодействий (ρ) от коэффициента α

В общем случае при поступательном движении системы из двух одинаковых по величине векторов () с разностью фаз 90° их равнодействующая:

,

где для данного угла tg45°=1

Если происходит вращательное движение или движение по спиральной динамике, то вектор () станет касательным вектором и образует угол вращения, для которого можно записать:

tg φ = С/R = =1.414213,                                                                                              (1)

где φ геодезический угол, равный 54.733°.

При =50% (рис.1) система имеет равновесное энтропийное состояние, для которого выполняется условие (в линейной интерпретации):

                                                                                                          (2)

Расчёт по этому уравнению дает значение коэффициента α, равное 12.1%, что соответствует приведенной номограмме (рис.1).

Многие явления и процессы в природе, технике и даже в экономике описываются аналогичными графиками, которые называются S-кривыми. Такие S-кривые и исходные номограммы являются графическими характеристиками неравновесной динамики изменения энтропийных составляющих [9].

3. Угловые характеристики энтропийных составляющих при вращательном и спиральном движении

При вращательном движении твердого тела (или математической точки) вокруг неподвижной оси вектор полного ускорения ( состоит из двух составляющих векторов: центростремительного ускорения ( и линейного ускорения ( - рисунок 2.

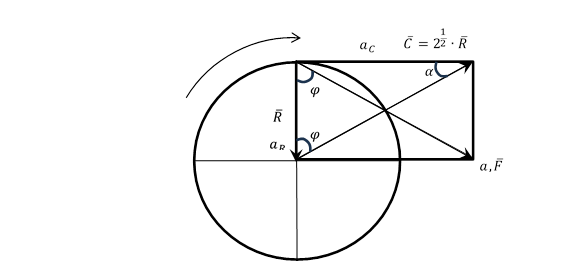
Рисунок 2. Кинематические характеристики вращательных движений

 – вектор центростремительного движения

 – вектор линейного (касательного) движения

 – центростремительное ускорение

 – линейное ускорение

 – полное ускорение

 – вектор полного взаимодействия.

Линейное ускорение () направлено от системы по касательной к траектории вращения. Поэтому вектор  является физической характеристикой негэнтропии по уравнению (1).

Центростремительное ускорение () направлено к центру вращения, и вектор  является физической характеристикой энтропийной составляющей по уравнению:

                                                                                                     (3)

где.

Таким образом базисные правила сложения энтропийных составляющих определяются геометрией исходных векторных величин через  и  , где используется принцип обратного соотношения величин  и . Изначально по геометрии этих векторов негэнтропийная составляющая (волновые взаимодействия) больше в 1,4142 раза, чем энтропийная величина (корпускулярное взаимодействие). В комплексных системах для сохранения этого правила выполняется алгебраическое сложение в волновых процессах, а в корпускулярных идет сложение обратных величин их составляющих.

4. Энтропийные соотношения в технических системах

Такие закономерности могут успешно применяться в технических новациях, например, при работе некоторых сельскохозяйственных машин, в частности при намотке льна-долгунца на основу. При этом энергетически наиболее эффективным является направление полного взаимодействия , которое будет выполняться под углом  по отношению к вектору , или под углом  по отношению к вектору . Так тутовый шелкопряд наматывает нить на основу под геодезическим углом , но по направлению полного взаимодействия . В космонавтике использование этого принципа приведено в работах [4, 5].

В этих работах используется понятие разрушающего напряжения при растяжении пластика нити на шаг ее намотки: σ_α – осевое, σ_β – окружное напряжения, которые заменяются пропорциональной им величиной N_α – осевое «усилие» и N_β – окружное «усилие». При этом выполняется уравнение:  

                                                                                                (4)

«Это условие позволяет получать равнонапряженную систему нитей с минимальной массой изделия» [5]. Армирование под углом φ снижает массу композитов на 22% (ANSYS Mechanical).

Поскольку такие энтропийные закономерности неизвестны широкой научной общественности, то их применение в практике явно недостаточное. А учитывать эти принципы необходимо в технологии приготовления гибридной продукции, состоящей из двух или более компонентов (или фракций). Например, при изготовлении молокосодержащих составов. Полученная таким способом продукция будет качественно лучше обычной.

В квантовой механике отношение магнитного момента частицы к ее механическому моменту называется магнитомеханическим (гиромагнитным) отношением – g. При этом g_s  2, если магнитный момент электрона обусловлен только спиновой составляющей и g = 1, если он создаётся орбитальным движением электронов. Магнитомеханическое отношение  коррелирует с , подтверждая связь спиновых и орбитальных взаимодействий.

В гармонических колебаниях тела отношение потенциальной энергии обусловленной квазиупругой силой к кинетической энергии равно tg²δ, то есть:

= tg²δ

где δ – угловая характеристика колебаний.

При условии равенства δ=φ система получает энтропийное равновесное состояние.

При вращательном движении касательное ускорение больше центростремительного в 2π раза. Применительно к исходной энтропийной модели по рисунку 2 выполняются уравнения:

                                                                                                            (5)

                                                                                                          (6)

Величина 2π характеризует один полный цикл процесса. Согласно второму уравнению, такой цикл есть переход от вектора центростремительного к вектору линейного ускорения (). Вектор  определяет направление поступательного движения. Поэтому данный цикл можно интерпретировать как переход от вращательного движения к поступательному с поглощением энергии, которая определяется энтропийным соотношением 1,4142. Очевидно, так происходит при взаимодействии света с веществом. Например, при явлении фотоэффекта. Электроны орбитального движения переходят на другую более высокую орбиталь (внутренний фотоэффект), или уходят за пределы атома (внешний фотоэффект). Если исходное излучение будет достаточно мощным, то возможно поступательное движение самого макрообъекта.

И в современной модели фотонного квантового двигателя через рабочее тело, которым является фотонный газ, пролетают сверхъизлучательные атомы. Такой двигатель, созданный корейскими физиками в Сеульском национальной университете [10], имеет высокий КПД, при этом результирующая энтропия процессов равна нулю. КПД фотонного двигателя достигает 85% при мощности лазера 10 кВт. А движущая активность создается за счет внутренних энтропийных конформационных процессов при переходе .

В наиболее простой модели фотонного двигателя, в патенте которого вписано: движущая сила создается за счет мощного лазера, лучи которого направляются на систему зеркал [11]. Но в таком двигателе, как в изолированной системе, результирующая энтропия тоже должна быть равна нулю, а тяговая сила создается за счет энтропийных внутренних конформационных процессов.

Еще пример: при полете космических аппаратов «Пионер-10» и «Пионер-11» было зафиксировано аномальное ускорение полета [10]. Предполагается, что оно вызвано анизотропией теплового излучения аппаратов [10]. Так, анизотропия теплового излучения спутников учитывается при определении параметров гравитации поля Земли [10]. Можно предполагать, что в этих и других аналогичных случаях движущую силу определяют энтропийные конформационные процессы.

Исследования и анализ проблем конформационной стабилизации физико-химических систем имеет большое практическое значение [12]. Применение энтропийных принципов и здесь может оказаться полезным. Особенно, если использовать специальные катализаторы, которые имеют оптимальные энтропийные характеристики.

5. Энтропийные постоянные в космологии

В общем случае, единая материализованная природная система проявляется в структурных процессах путем взаимодействия двух противоположных субстанций: энтропии и негэнтропии. При этом может осуществляться энергетический переход между ними, например, переход от негэнтропии (С) к энтропии (R), при котором меняется поступательное движение на вращательное. А это значит, что идет процесс конформации стабильных атомно-молекулярных структур.

Можно предположить, что такие явления энергетически и конструктивно определяют основные этапы космологических изменений во Вселенной. В начале, по данным многих исследований [13,14,15], Вселенная представляла собой сингулярную систему с высокими температурой и степенью плотности, перемещающуюся в пространстве поступательно, и с большой скоростью. Также установлены взаимодействия с так называемой «тёмной» материей, энергия которой с противоположными свойствами получила название отрицательной [16,17].

На основе исходных энтропийных положений изначально были две противоположные энтропийные субстанции: негэнтропийная – это сингулярная система с её супер-максимальной энергией, и энтропийная субстанция – это система «темной» материи с её «отрицательной энергией». Взаимодействие таких субсистем при супер-больших массах могло иметь взрывной характер. А происходил такой процесс по энергетически наиболее выгодному переходу от C к R. И в исходной сингулярной системе стимулировались процессы перехода от поступательного к вращательному движению во всех микро-областях ее массы [18].

На первых этапах эволюции могло идти образование элементарных частиц, а на более поздних стадиях, в условиях резких температурных изменений – возникновение атомных центров, с орбитальным движением электронов. В современных научных исследованиях доказано [13,14], что процесс рождения и развития Вселенной происходил в несколько основных этапов, которые энергетически подтверждаются законом Хаббла и его постоянными параметрами [15,19] (таблица 2).

Таблица 2.

Параметры Хаббла по стадиям эволюции Вселенной

На основе этих параметров Хаббла был получен закон ускоренного расширения Вселенной [15,19]. Каждый параметр в данной стадии имеет постоянный числовой коэффициент. Проведённые сопоставления показали, что он имеет прямую математическую связь с основным энтропийным параметром tg φ с точностью от 0% до 5,7% (таблица 3).

Таблица 3.

Соотношения энтропийной постоянной и коэффициентов Хаббла

Но числовые значения параметров Хаббла, рассчитанные различными методиками, имеют примерно такую же относительную разность между собой [15,19].

Установленное равенство постоянных коэффициентов Хаббла с основным энтропийным параметром доказывает то, что рождение и развитие Вселенной шло и идет по энтропийным принципам.

Заключение

Данный подход не является принципиально новым, и приведенные примеры - не единичны. В 1943 году Э. Шредингер в книге «Что такое жизнь?» объяснил, что в живой системе отрицательная энтропия, создаваемая организмом, уравновешивает поток положительной энтропии. Так, еще тысячи лет назад китайская медицина установила, что все явления мира и природы можно рассматривать как взаимодействие двух противоположных начал единой действительности. А в диалектике выполняется принцип единства и борьбы противоположностей.

В химической кинетике выполняется принцип Ле-Шателье: При внешнем воздействии на систему, находящуюся в равновесии, равновесие будет сдвигаться в направлении того процесса, который противодействует данному воздействию.

Условия энтропийной методологии находятся в соответствии с Принципом дополнительности Н. Бора: для полного описания квантово-механических явлений необходимо применять два взаимоисключающих (дополнительных) набора классических понятий, совокупность которых дает исчерпывающую информацию об этих явлениях как о целостных. Например, описание объекта как частицы и как волны.

Таким образом, исходные энтропийные соотношения определяют общие принципы многих физико-химических закономерностей.

Выводы:

1. Геометрически-геодезический угол (φ = 54.733°) определяется как отношение двух составляющих: негэнтропийной 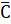 (линейное ускорение, 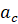) и энтропийной  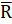(центростремительное ускорение 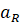), где tg φ =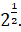
2. Показано, что переход 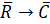 соответствует смене вращательного движения на поступательное с поглощением энергии. И возможен обратный переход  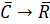от поступательного движения к вращательному.
3. На примерах армирования композитных материалов, фотонных двигателей и космологических данных продемонстрирована универсальность угла φ в системах с доминированием энтропийных переходов.
4. Установлена прямая математическая связь tg φ с постоянными коэффициентами в космологических параметрах Хаббла.
5. Динамика энтропийных взаимодействий определяет конформационные процессы рождения и развития Вселенной.

Благодарности

Благодарю специалиста Романченко Артема Павловича за предоставление ценной информации при редактировании текста статьи.