Разработка программного комплекса пространственной модели стержня в геометрически нелинейной постановке в среде Microsoft Excel
Конференция: VI Международная заочная научно-практическая конференция "Научный форум: технические и физико-математические науки"
Секция: Строительство и архитектура

VI Международная заочная научно-практическая конференция "Научный форум: технические и физико-математические науки"
Разработка программного комплекса пространственной модели стержня в геометрически нелинейной постановке в среде Microsoft Excel
Development of software geometric nonlinear 3D rod model in Microsoft Excel
Alexandr Faletyonok
undergraduate of The Siberian State Automobile and Highway University – SibADI, Russia, Omsk
Sergey Makeev
doctor of Engineering Sciences, professor in The Siberian State Automobile and Highway University, SibADI, Russia, Omsk
Аннотация. В статье рассматриваются разработка программного комплекса на основе математической модели стержня в геометрически нелинейной постановки при пространственном загружении. Разрабатывается программная надстройка в среде программирования MS Visial Basic for Application для реализации последовательного нелинейного увеличения прикладываемой нагрузки. Для проверки работы программного комплекса производится расчет потери устойчивости плоской формы деформирования консольной балки, нагруженной сосредоточенной на свободном конце нагрузкой.
Abstract. The article describes development of software in Microsoft Excel based on geometric nonlinear 3D rod model. Program software is created in development environment MS Visial Basic for Application and implements nonlinear load increase. The calculation of the cantilever beam buckling is done for test the created software.
Ключевые слова: разработка программного комплекса в среде Microsoft Excel, математическая модель стержня при пространственном загружении, геометрическая нелинейность.
Keywords: development of software in Microsoft Excel, geometric nonlinear 3D rod model, the geometric nonlinearity.
Текст статьи.
Действующие строительные правила СП 16.13330.2011 «Стальные конструкции» предписывают рассчитывать стальные пространственные конструкции с учетом геометрической и физической нелинейности [1, п. 4.2.5]. В рамках данной работы ограничимся геометрической нелинейностью. Для реализации этой цели разрабатывается программный комплекс на основе математической модели стержней в геометрически нелинейной постановке, изложенной в работе В.А, Светлицкого [2].
В математической модели рассматривается две ортогональные системы координат (рис. 1):
· неподвижная декартовая система {ij} с единичными векторами ij, относительно которой определяется первоначальное положение стержня;
· подвижная декартовая система {ei} с единичными векторами ei, жестко связанной с осевой линией стержня.
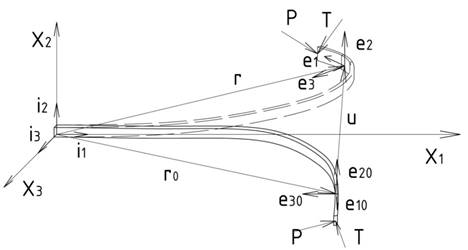
Рисунок 1. Размещение ортогональных систем координат математической модели
На рис. 1 показаны два положения стержня: положение 1 соответствует ненагруженному состоянию (естественному), под 2-ым положением изображено положение стержня в нагруженном состоянии. Под действием медленно нарастающих сил Pi и моментов Ti (в математической модели рассматривается статика), заданных различными законами, стержень деформируется из положения 1 в состояние 2.
Система нелинейных уравнений равновесия стержня в геометрически нелинейной постановке при пространственном загружении имеет вид:
![]() , (1)
, (1)
![]() , (2)
, (2)
![]() , (3)
, (3)
![]() , (4)
, (4)
![]() , (5)
, (5)
где: 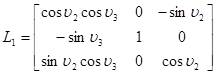 ;
;
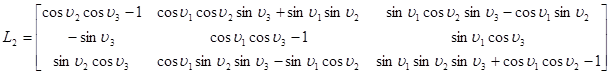
Аппроксимируя производные в функциях (1) – (5) с помощью отношения конечных разностей (а именно, левых разностей), получаем следующие функции для численного интегрирования в проекциях на связанные оси:
· для внутренних усилий:
![]() ; (6)
; (6)
![]() ; (7)
; (7)
![]() ; (8)
; (8)
Подставляя выражения кривизн (3) в уравнения моментов (4), уменьшим количество уравнений в итерационном цикле:
· -для кривизн:
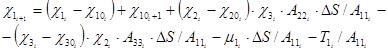 ; (9)
; (9)
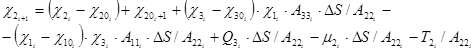 ; (10)
; (10)
 ; (11)
; (11)
· для углов поворота подвижных осей (связанных с поперечными сечениями элементов):
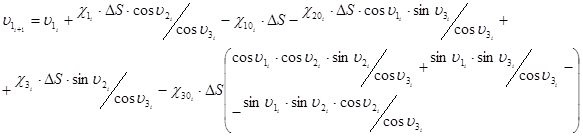 ; (12)
; (12)
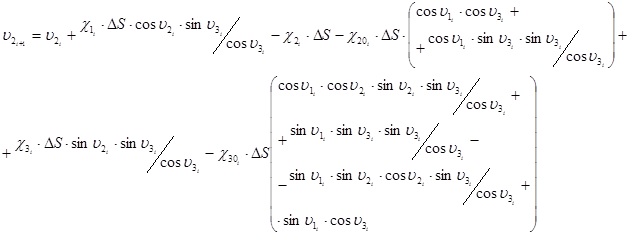 ; (13)
; (13)
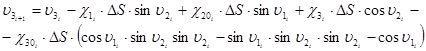 . (14)
. (14)
Для перемещений:
![]() ; (15)
; (15)
![]() ; (16)
; (16)
![]() ; (17)
; (17)
Стандартная надстройка программного комплекса Microsoft Excel «Поиск решения» позволяет определить перемещение, а также внутренние усилия от заданной определенной внешней нагрузки, т.е. на определенном этапе загружения.
Однако, для изучения поведения стержня в зависимости от увеличивающейся нагрузки существует необходимость нелинейного увеличения внешней нагрузки. Итерационный цикл нелинейного увеличения действующей нагрузки (для отслеживания деформирования стержня от увеличения нагрузки) программируется возможностями языка Microsoft Visual Basic for Application.
По результатам выполнения разработанной программы создается несколько десятков листов рабочей книги Excel отдельных этапов последовательного нелинейного увеличения внешней нагрузки вплоть до критического значения, а также до определенного процента в закритической стадии.
В результате работы программы реализуется итерационный цикл нелинейного увеличения внешней нагрузки, представленный на рис. 2.

Рисунок 2. График нелинейного увеличения внешней нагрузки в ходе итерационного цикла программной надстройки
Для проверки работы программного комплекса проводится численный эксперимент потери устойчивости плоской формы деформирования консольно защемленной балки прямоугольного поперечного сечения с размерами bxh=2х20 мм, пролетом l=500 мм.
Загружение производится постоянной нагрузкой с последовательным нелинейным увеличением интенсивности (рис. 2).
Значение критической нагрузки для консольной балки с сосредоточенной на свободном конце нагрузкой предварительно определяется по формулам строительной механики [3, ф. 6.20]:
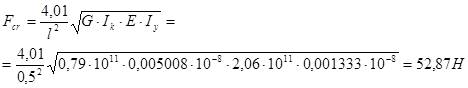 , (18)
, (18)
где: G=0,79*105 МПа – модуль сдвига прокатной стали [1, табл. Г.10];
![]() – геометрическая характеристика сечения при кручении: для стержня прямоугольного сечения [4, табл. 2.2];
– геометрическая характеристика сечения при кручении: для стержня прямоугольного сечения [4, табл. 2.2];
β=0,313 – коэффициент Сен-Венана при кручении стержней прямоугольного поперечного сечения с отношением h/b=10;
E=2,06*105 МПа – модуль упругости прокатной стали [1, табл. Г.10];
![]() – момент инерции поперечного сечения относительно вертикальной оси (относительно вектора e2 базиса, связанного с поперечным сечением).
– момент инерции поперечного сечения относительно вертикальной оси (относительно вектора e2 базиса, связанного с поперечным сечением).

Рисунок 3. Деформации свободного конца консольной балки при потере устойчивости плоской формы деформирования

Рисунок 4. Внутренние усилия в свободном конце консольной балки при потере устойчивости плоской формы деформирования
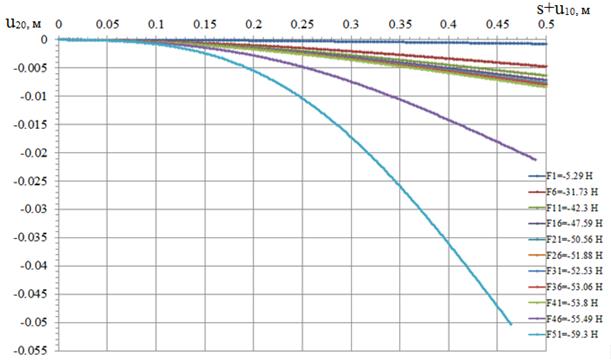
Рисунок 5. Деформирование консоли в вертикальной плоскости при последовательном увеличении нагрузки
Разработанный программный комплекс реализует математическую модель стержней в пространстве в геометрически нелинейной постановке и позволяет:
· изучать поведение отдельных прямолинейных стержней вплоть до критической нагрузки, а также в закритической стадии в геометрически нелинейной постановке (т.е. учитывает влияние фактических перемещений на перераспределение усилий) при пространственном загружении;
· изучать поведение отдельных криволинейных стержней (в виде криволинейного стержня возможно представить отдельный профиль арочной конструкции, а также элементы сложной конфигурации) вплоть до критической нагрузки, а также в закритической стадии в геометрически нелинейной постановке (т.е. учитывает влияние фактических перемещений на перераспределение усилий) при пространственном загружении;
· учитывать влияние преднапряжения стержней на их поведение при нагружении, а также на конечную несущую способность;
· учитывать фактические геометрические характеристики (т.е. дефекты и повреждения, выявленные при обследовании конструкций) и оценивать их влияние на поведение, а также конечную несущую способность при нагружении стержня пространственной нагрузкой;
· позволяет изучать поведение плоских стержневых систем (ферм), а также пространственных систем в геометрически нелинейной постановке, а также влияние преднапряжения, дефектов на поведение и, в конечном счете, на несущую способность стержневых систем.


