Методика обоснования сроков развертывания дорожно-строительных работ при переходе зимних автодорог через болота

Method of justifying the timing of the deployment of road construction works in the transition of winter roads through bogs

Аlexander Menshikov

Сandidate of Engineering science, associate professor of Higher School of Engineering, Nortern (Arctic) federal university named after M.V. Lomonosov, Russia, Arkhangelsk

 Alexander Korolev

Мaster of science of Higher School of Engineering  Nortern (Arctic) federal university named after M.V. Lomonosov, Russia, Arkhangelsk

Аннотация. При планировании дорожно-строительных работ на болотах в зимний период встает вопрос о сроке промерзания болота, когда становится возможным движение по его поверхности технологических или дорожно-строительных машин. В статье рассматривается методика определения даты начала работ на основе прочностного и теплотехнического расчетов.

Abstract. When planning road construction in marshes in winter, the question arises of the period when the swamp freezes, when it becomes possible to move cargo, technological or road-building machines along its surface. The technique for determining the starting date for work based on strength and heat engineering calculations is considered.

Ключевые слова: зимние автомобильные дороги; строительство дороги через болото; прочность основания; теплотехнический расчет.

Keywords: winter roads; road construction through the swamp; strength of the base; heat engineering calculation.

Прочность поверхности торфа под действием заданной внешней нагрузки (трелевочный трактор, бульдозер, экскаватор или многооперационные лесосечные машины) зависит от типа болота, его несущей способности. Безопасный проход и работа тяжелой техники на болоте возможны только при достаточной толщине слоя мерзлого торфа, способной выдержать нагрузки от современных машин.

Толщину слоя мерзлого торфа, допускающую движение по поверхности транспортных средств, ориентировочно можно определить по формуле [2, с.34]

                            ,                                                      (1)

где     Н_р – минимальная по условию прочности толщина слоя мерзлого торфа, см;

           Р – сила тяжести на поверхности проезжей части от транспортных средств, кН;

           С – коэффициент постели талого торфа, Н/см³. Зависит от типа болота;

           Θ – расчетная температура на поверхности проезжей части, ˚С;

           В – ширина проезжей части, см.     

В результате процессов теплообмена, происходящих на поверхности болот, формируется тепловой поток и, соответственно, температурное поле болота. Температурный режим болота зависит от метеорологических условий, составляющих теплового баланса, высоты и физических свойств снежного покрова, наличия растительного слоя на поверхности торфа.

Метеорологические элементы, особенно температура воздуха и снежный покров, в течение периода промерзания не остаются неизменными.

Температура поверхности в природных условиях является результирующей характеристикой сложного тепломассообмена покрова и толщи торфа с приземным слоем атмосферы согласно схеме на рис.1.

В реальных условиях располагают температурой приземного слоя воздуха, определяемой сетью метеостанций гидрометеослужбы. Поэтому в практике теплотехнических расчетов обычно используют связь температуры дневной поверхности с температурой воздуха и составляющими теплового баланса, из которых в зимний период учитывают радиационную поправку Δt_R, отепляющее влияние снежного покрова Δt_сн (с учетом постепенного увеличения высоты снега пропорционально понижению температуры воздуха) и наличие рас­тительного покрова Δt_рс.                         

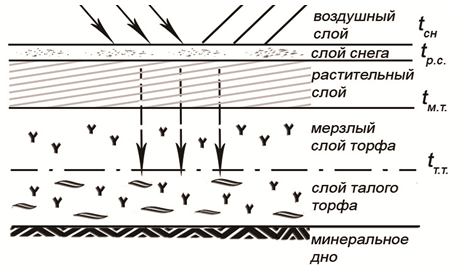
Рисунок 1. Схема тепломассообмена промерзающей залежи с атмосферой

Радиационная поправка Δt_R рассчитывается как разность между температурой по­верхности торфа, очищенной от снега и растительного покрова, и температурой воздуха на уровне 2,0 (1,5) м по формуле [3, с.2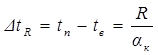2]

                                            ,                                                                                     (2)

где  t_в  – температура воздуха, ˚С;

       t_п – температура поверхности земли, ˚С;

        R – радиационный баланс земной поверхности, ккал/м²·час. Среднеширотная (для широты 62˚ РФ) сумма радиационного баланса в ноябре-декабре может быть принята по данным [3];

       α_к – коэффициент конвективного теплообмена, ккал/м²·град·час. Для поверхностей с растительным покровом и снегом α_к = 8…13,5 [4, с.74].

В метеорологических исследованиях годовой ход температуры воздуха часто представляют гармоническими функциями в виде тригонометрического полинома Фурье или частных случаев: синус- и косинус-аппроксимаций.

Снежный покров, с одной стороны, увеличивает альбедо поверхности земли, что приводит к уменьшению поглощения лучистой энергии и к понижению среднегодо­вых температур поверхности грунта. С другой стороны, снежный покров как естественный теплоизолятор предохраняет массив от теплопотерь в зим­нее время года и способствует замедлению промерзания торфа, что приводит к повышению среднегодовых темпера­тур в сравнении с t_в. График среднемноголетних данных наблюдений за высотой снежного покрова h_сн обычно аппроксимируют гладкими алгебраическими полиномами вида , где τ – порядковый номер даты в периоде.

Влияние растительного покрова на глубину сезонного промерза­ния и оттаивания и на температурный режим болот оказывается через обусловленные им изменения теплообмена между почвой и атмосфе­рой, а также через влагообмен между атмосферой и почвой. В результате среднегодовая температура воздуха на поверхности напочвенного растительного покрова (мох, травяной покров, лесная подстилка и т. п.) на 0,2…0,5 °С выше среднегодовой температуры воздуха на высоте 1,5 м [4].

Для приближенных расчетов теплового влияния снега и растительного покрова возможно использовать формулы проф. В.И. Кудрявцева [3, с.157]:

                                                                                                                       (3)

                                                                                                                            (4)

                                                                                                                    (5)

                                                                                                                    (6)

                                      ,                                                                                            (7)

                                      ,                                                                                            (8)

где  А_в, А_рс –  амплитуда годовых колебаний соответственно температуры воздуха и температуры на поверхности растительного покрова, ˚С;

     ΔА₁, ΔА₂ – разница в среднесуточных температурах воздуха на поверхности растительного покрова и под ним соответственно за холодное и теплое время года, ˚С;

       h_сн, h_рс – соответственно толщина слоя снега и толщина растительного слоя, м;

       Т – продолжительность периода, равного 1 году, час;

       τ₁, τ₂ – продолжительность периодов соответственно с отрицательными и положительными температурами воздуха, час;

       К_сн – коэффициент температуропроводности снега, м²/час;

      – коэффициенты температуропроводности растительного покрова соответственно в талом и мерзлом состоянии, м²/час.

При расчете А₁ и А₂ значения t_рс  и  t_в принимают с учетом знака.

С учетом всех поправок расчетный температурный режим поверх­ности несущей торфяной залежи на болоте определяется по формуле

                                            t₀ = t_в + Δt_R + Δt_сн+ Δt_рс.                                                                                   (9)

Слагаемые формулы (9) также принимают с учетом знаков.  

При решении задачи определения глубины промерзания решается уравнение теплового баланса с учетом условий теплообмена, тепло- и массопереноса, а также количества тепла, затрачиваемого или выделяемого в процессе фазовых переходов воды. Теоретическое решение задачи определения глубины промерзания в однородной изотропной среде, известной как «классическая задача Стефана» [3, с.53], одним из первых в 1889 г. получил в общем виде австрийский математик Й. Стефан.

На основе решения Й. Стефана А.Г. Дорофеев [1, с.13] вывел зависимость для определения времени промерзания τ (в сутках) зимней дороги на переходе через болото с открытой поверхностью, которая с учетом отепляющих факторов уточнена нами и используется для практических расчетов в виде

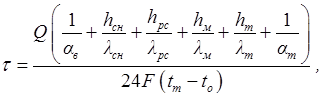                                                                                                  (10)

где  Q – количество холода, необходимого для замерзания верхнего слоя торфа до нормированной температуры -0,3 ˚С на границе раздела зон, ккал;

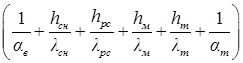– термическое сопротивление среды, м²·˚С/ккал;

α_в – коэффициент теплопередачи от воздуха к открытой поверхности торфяной залежи, ккал/(м²·˚С);

α_m – коэффициент теплопередачи от нижней границы мерзлого слоя торфяной залежи к поверхности талого слоя торфяной залежи, ккал/(м²·˚С). Определяется по формуле

                                                     α_т = λ_т/h_к.т ,                                                                                            (11)

где h_к.т – толщина слоя торфа, участвующего в конвективном теплообмене, м;

t_в – температура воздуха согласно метеорологическим данным по району, ˚С;

t_т – температура на границе раздела мерзлого и талого слоев торфа, ˚С.

       Принимается согласно СНиП 2.02.04-88 t_т=-0,3;

λ_сн – коэффициент теплопроводности снега, ккал/(м·ч·˚С). Принимается в зависимости от плотности снега в естественном состоянии;

λ_рс, λ_т, λ_м – коэффициенты теплопроводности соответственно растительного слоя, талого и мерзлого торфа, ккал/(м·ч·˚С);

h_м, h_т – изменяющиеся толщины зон соответственно мерзлого и талого торфа, м;

F – расчетная площадь теплопередачи, м², F = 1 м² [1, с.10].

По данной методике нами выполнены расчеты для районов, где имеются данные регулярных метеонаблюдений за температурой и снегонакоплением.