Исследование регулятора объединенного принципа максимума, оптимального по «минимуму расхода управления

Study of the regulator based on the combined principle of maximum, optimal control flow rate

Igor Pugachev

postgraduate Don state Technical University, Russia, Rostov– on– Don

Irina Pavlova

Candidate of Engineering Sciences, docent Don Cossack state Institute of food technology and business (branch) Federal state budgetary educational institution of higher professional education "Moscow state University of technologies and management named K. G. Razumovskiy, Russia, Rostov– on– Don

Salih Bilal Ahmed Salih

undergraduate Don state Technical University, Russia, Rostov– on– Don

«Работа выполнена по грантам РФФИ № 18-38-00937 мол_а, № 18-08-01494 А»

Аннотация. В данной работе предлагается новый метод аналитического конструирования оптимального регулятора, разработанный на основе объединенного принципе максимума. Этот метод требует решения краевой
задачи и не подрузомевает использование функции Беллмана.

Abstract. In this paper, we propose a new method of analytical design of the optimal regulator, based on the combined principle of maximum. Its application requires the solution of the boundary value problem and does not involve the use of Bellman function.

Ключевые слова: оптимальный регулятор; объединенный принцип максимума; динамическая система; краевая задача.

Keywords: optimal regulator; combined maximum principle; boundary value problem.

Введение. Для достижения эффективного функционирования современных управляющих систем в трудных уловиях эксплуатации, необходимо постоянно контролировать их параметры. Это обеспечивает своевременную корректировку управляющих воздействий для дальнейшей стабилизации исправного состояния. Параметры оптимального регулятора, высчитаваются по законам оптимального управления и минимизируют заданный функционал. Поэтому, в условиях, когда задача синтеза оптимального управления является некласической, эффективным методом является объединенный принцип максимума[1]. В случаях, когда синтез закона оптимального управления рассчитывается по критерию Летова- Калмана [2-5], или функционала обощенной работы Красовского А.А.[5]. В таких ситуациях, необходимо что бы, в законы управления были включены функции Беллмана в виде некоторой определенно- положительной формы. В известных принципах Л.С. Понтрягина, Р. Беллмана и методе Лагранжа [2-8] движение объекта записывается в виде систем дифференциальных уравнений, а условия оптимальности устанавливаются для фиксированного момента времени, то есть отыскиваются в начале программы оптимального управления. При этом решение задачи синтеза требует дополнительных гипотез.

В данной работе предлается новый метод аналитического конструирования оптимального регулятора. Для его реализации необходимо перейти от оптимизационной задачи к краевой. Краевая задача не подрузомевает использования функции Беллмана.

Постановка задачи. Необходимо синтезировать в аналитическом виде закон оптимального управления динамической системой. При условии, что движение обусловленно принципом Гамильтона- Остраградского из условия минимизации функционала:

                                                                             (1)

где     - обобщенные координаты;

 - искомые управления;

 - фиксированный момент времени,

 - число степеней свободы динамической системы.

Метод приведения от задачи синтеза оптимального управления к краевой задаче. Следует упомянуть, что в данном исследовании, разработка метода ограничена линейными уравнениями движения.

В таком случае, при использовании процедуры объединенного принципа максимума к расширенному функционалу [6-8], получаем:

,                                                                                       (2)

где     - кинетическая энергия;

          - работа обобщенных сил,

 - неопределенный множитель Лагранжа.

Исходя из этого, получаем, что первая асинхронная вариация этого функционала будет иметь вид:

.

При условии, что время  фиксировано, то из этого получается, что первое слагаемое равно нулю, а из второго слагаемого получаются тождества:

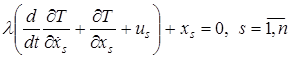,                                                                            (3)

.                                                                                           (4)

При проведении повторного синхронного варьирования уравнения(3), устанавливается связь между вариацией тректории и вариацией управления:

                                                                               (5)

В дальнейшем, после интегрирования по частям[9-14] и подстановка  из (3), и  из (4), в условие оптимальности управления, приводит задачу синтеза оптимального управления к краевой задаче для фазовых координат.

Тогда, вариационная форма уравнений краевой задачи получает вид:

                                                     (6)

Исходя из этого, для конкретных случаев задач синтеза, необходимо проводить развертываение этого уравнения. После того, как решение краевой задачи будет найдено, оптимальное управление получаем из уравнения:

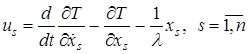.                                                                                       (7)

Пример. Процедура синтеза в аналитическом виде закона оптимального управления[8-10], который стабилизирует движение объекта  для критерия качества, принимает вид:

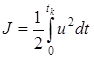.                                                                                                      (8)

При этом, движение объекта задано уравнением:

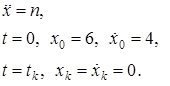                                                                                           (9)

Поэтому, в соотвествии с вариационным уравнением (6) дифференциальное уравнение двухточечной краевой задачи имеет вид:

.                                                                                                        (10)

Из этого следует, что решение принимает вид:

                                                                                       (11)

Из краевых условий (9), находится постоянные интегрирования, которые принимают вид:

                                                                          (12)

Для исключения особенностей в конечный момент времени, в отличии от известного решения, предлагается использовать обратную связь:

.                                                                                      (13)

где  - константа.

Полученные результаты расчетов, при заданных краевых условиях (9), предствлены на рисунке 1 (графиками ), на рисунке 2 (графиками ) и на рисунке 3 (фазовым портретом движения объекта).

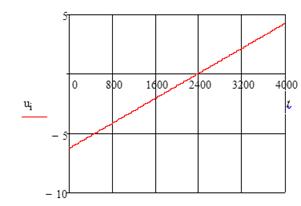
Рисунок 1. Результаты расчетов   .            Рисунок 2. Результаты расчетов

Рисунок 3. Фазовым портрет движения объекта 

Заключение. Таким образом предложенное эвристическое решение в этой работе, позволяет исключить особенность в конечный момент времени. Это является существенным достоинством предлагаемого подхода. При этом, объединенный принцип максимума является более универсальным в отношении Принципа максимума Понтрягина и решает задачу синтеза для любых Лагранжевых систем.