Применение нейронных сетей типа Adaline в качестве средства математического моделирования

APPLICATION OF ADALINE-TYPE NEURAL NETWORKS AS A MATHEMATICAL MODELING TOOL

Yevgeniy Nazarov

senior lecturer, Surgut State University, Russia, Surgut

Аннотация. В статье рассматриваются особенности алгоритма создания нейронной сети типа Adaline для её применения в качестве математической модели треморограмм кистей рук. Ключевое значение для выполнения одного из этапов упомянутого алгоритма имеют такие параметры, как скорость обучения нейронной сети рассматриваемого типа для указанной задачи и количество значений входного сигнала, используемых для определения целевого значения. Для нахождения наилучших значений упомянутых параметров были разработаны соответствующие функции, описание которых также представлено в данной статье.

Abstract. The article discusses the specifics of the algorithm for creating a neural network of the Adaline type for its application as a mathematical model of tremorograms of a hands. Parameters such as a learning rate of a neural network of the type under consideration for the specified task and a number of input signal values used to determine a target value are of key importance for performing one of the stages of the mentioned algorithm. To find the best values of these parameters, the corresponding functions were developed, the description of which is also presented in this article.

Ключевые слова: adaline; адаптивный линейный нейрон; нейронная сеть; математическая модель; аппроксимация.

Keywords: adaptive linear neuron; neural network; mathematical model; approximation.

Введение

Математические модели в соответствии с [2, с.39 – 40] «представляют собой формализованные описания объекта или системы с помощью некоторого абстрактного языка, например, в виде совокупности математических соотношений или схемы алгоритма. Различают следующие виды математического моделирования: вербальное (словесное), графические, табличные, аналитические и алгоритмические. Нередко математические модели оказываются пригодными для описания множества систем и явлений в самых различных областях науки, техники и экономики». Одним из подходов к представлению модели течения какого-либо процесса с возможностью прогнозирования его хода является использование нейронной сети. Кроме того, согласно [4, с. 43 – 44] «выполняемые сетью функции можно распределить на несколько основных групп: аппроксимации и интерполяции; распознавания и классификации образов; сжатия данных; прогнозирования; идентификации; управления; ассоциации. В каждом из названных приложений нейронная сеть играет роль универсального аппроксиматора функции от нескольких переменных, реализуя нелинейную функцию , где х – это входной вектор, y – реализация векторной функции нескольких переменных».

Исходные данные

Одним из примеров функций, описанных выше, является треморограмма кистей рук, которая представляет собой числовой вектор-столбец из 500 чисел с плавающей точкой, каждое из которых принимает значение в пределах от -2 до 2. В качестве исходных данных для построения моделей использовались наборы треморограмм кистей рук, полученные при различных уровнях нагрузки: отсутствие, постоянная, периодическая. Все наборы состоят из множества файлов, содержащих по 15 треморограмм каждый. Фрагмент описанных исходных данных представлен в таблице 1.

Таблица 1.

Фрагмент исходных данных

В качестве нейронной сети, которая могла бы наилучшим образом справиться с задачей аппроксимации рассматриваемых исходных данных и, соответственно, получения их математической модели, была выбрана нейронная сеть, образованная адаптивными линейными нейронами (сеть типа ADALINE). Основными факторами, определившими выбор в пользу упомянутой сети, были следующие:

• возможность обучения с учителем;
• минимизация отклонения выходного сигнала сети от целевого заложена в процессе обучения сети;
• достаточно простая архитектура по сравнению с другими сетями, которые могут быть использованы для решения подобных задач.

Структурная схема и варианты уравнений для расчета весовых коэффициентов адаптивного линейного нейрона представлены в работе [3, с. 32 – 34].

Алгоритм создания нейронной сети ADALINE

Для создания нейронной сети, описывающей треморограму, использовалась библиотека Neural Network Toolbox системы MATLAB. Согласно [1] для создания сети типа ADALINE необходимо выполнить следующую цепочку действий:

• Задать исходные и целевые данные;
• Подготовить данные для нейронной сети;
• Определить нейронную сеть типа ADALINE;
• Обучить созданную сеть работе с подготовленными данными.

Задание исходных и целевых данных

Поскольку создаваемая нейронная сеть по итогу должна была представлять собой математическое описание треморограмм, то в качестве исходных и целевых данных был взят один и тот же массив значений.

Подготовка данных для нейронной сети

Так как значения исходных данных были записаны в файле в виде вектор-столбца, а алгоритм обучения сети требует последовательной «подачи» данных на входы нейронной сети, то в рамках данного этапа выполнялось преобразование считанного массива значений из вектор-столбца в вектор-строку.

Создание нейронной сети типа ADALINE

Создание нейронной сети выполнялось в 2 этапа:

• задание скорости обучения и количества значений входного сигнала, используемых для определения целевого значения. Для определения оптимальных значений указанных параметров были разработаны функции и проведены серии экспериментов, результаты которых отражены в последующих пунктах данной работы;
• вызов функции, создающей сеть с заданной структурой на основании параметров из предыдущего пункта.

Обучение нейронной сети

Обучение сети согласно [1] производится следующим образом. На каждом шаге обучения на вход нейронной сети подается один элемент последовательности входных значений. При этом происходит обновление весовых коэффициентов каждого входа и отклонения суммирующей функции. В результате обновление указанных коэффициентов происходит столько раз, сколько точек данных подается на вход нейронной сети. 

Функция аппроксимации исходных данных

Для реализации алгоритма создания нейронной сети ADALINE, описанного в предыдущем пункте, была разработана функция, в результате работы которой формируется нейронная сеть, наилучшим образом аппроксимирующая заданный сигнал.  Данная функция включает в себя выполнение действий по считываю исходных данных, вычислению оптимальной скорости обучения, определению количества значений входного сигнала, используемых для определения целевого значения, созданию сети. Для более полной оценки качества аппроксимации нейронной сетью исходного набора значений, в рассматриваемую функцию дополнительно была включена реализация следующих действий:

• сохранение весовых коэффициентов и величины рассогласования выходного сигнала сети с исходными данными в массив для обработки.
• вычисление некоторых общих статистических показателей рассогласования фактического значения с целевым: минимальное и максимальное значение, среднее значение, стандартное отклонение, мода.
• при необходимости выполняется построение следующих графиков:

i.исходного и предсказанного сигнала на одной плоскости. Пример представлен на рисунке 1.

ii.рассогласования исходного и предсказанного сигналов. Пример представлен на рисунке 2.

iii.изменения скорости обучения сети для массивов данных, входящих в серию измерений. Пример представлен на рисунке 3.

iv.изменения весовых коэффициентов. Пример представлен на рисунке 4.

v.изменения коэффициента отклонения суммирующей функции. Пример представлен на рисунке 5.

• запись значения скорости обучения, весовых коэффициентов, коэффициента отклонения суммирующей функции в текстовые файлы.

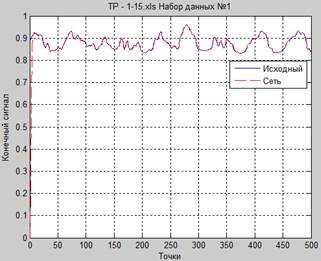
Рисунок 1. График исходного и предсказанного сигнала

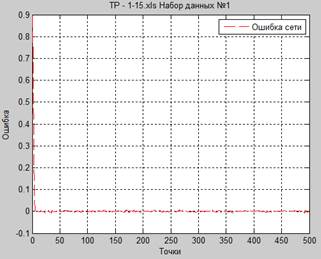
Рисунок 2. График разницы исходного и предсказанного сигналов

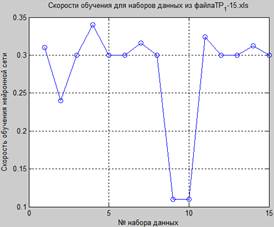
Рисунок 3. График изменения скорости обучения сети для массивов данных

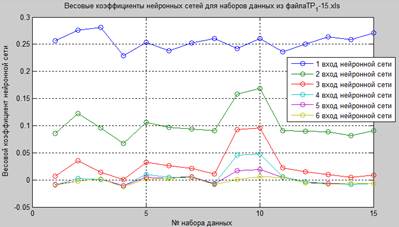
Рисунок 4. График изменения весовых коэффициентов

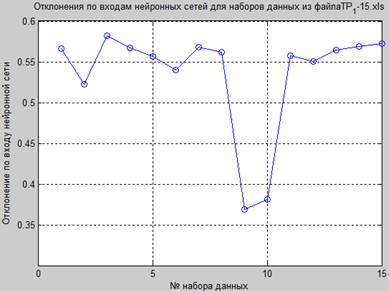
Рисунок 5. График изменения коэффициента отклонения суммирующей функции

Определение оптимальной скорости обучения нейронной сети

Очевидно, что скорость обучения нейронной сети является одним из главных факторов, оказывающих влияние на то, какое количество циклов обучения ей потребуется, чтобы свести ошибку в выходном сигнале к минимуму. Кроме того, параметр скорости обучения влияет и на точность работы сети. Например, если для него задано слишком большое значение, то это приведет к плохому качеству обучения и значительным ошибкам на выходе. Поскольку заранее неизвестно с каким набором данных предстоит работать сети, то целесообразно определять скорость динамически, т.е. в зависимости от содержания массива. Для этого перед созданием сети, непосредственно моделирующей требуемый сигнал, достаточно предварительно определить такое значение скорости обучения, при котором сеть будет обучаться максимально быстро и с минимальным ущербом для точности результата.

Вычисление коэффициента скорости обучения нейронной сети выполнялось в несколько этапов с помощью разработанной для этого функции. Здесь следует отметить, что количество этапов может быть как расширено с целью дальнейшего увеличения точности определяемого показателя, так и, наоборот, уменьшено. Суть выполняемых действий на каждом из этапов одинакова, а изменения претерпевают лишь пределы, в которых производятся вычисления:

• 1 этап: 0.001 – 0.6. Шаг перемещения по диапазону составляет 0.1.
• 2 этап: в зависимости от результатов предыдущего этапа. Например, если для коэффициента было установлено значение 0.4, то поиск выполняется в пределах 0.4 – 0.5. Шаг перемещения по диапазону составляет 0.01.
• 3 этап: в зависимости от результатов предыдущего этапа. Например, если для коэффициента было установлено значение 0.43, то поиск выполняется в пределах 0.430 – 0.440. Шаг перемещения по диапазону составляет 0.001.

Подобное вычисление скорости обучения выполнялось отдельно для каждого из наборов данных. При этом все коэффициенты для удобства дальнейшей работы сохранялись в одном массиве под соответствующими порядковыми номерами. Максимальное значение скорости обучения (0.6), обозначенное в первом этапе вычисления скорости, было установлено в ходе серии предварительных экспериментов, выходящих за рамки данной работы.

Сама же функция вычисления коэффициента скорости обучения нейронной сети в качестве входных значений получала следующий набор параметров: количество значений входного сигнала, используемых для определения целевого значения, целевой вектор (массив данных для обучения сети), левый предел диапазона для поиска коэффициента, шаг перемещения по диапазону, правый предел диапазона для поиска коэффициента. Алгоритм работы рассматриваемой функции был организован следующим образом. Сначала осуществлялось циклическое выполнение блока действий:

• Создание нейронной сети с заданным числом значений входного сигнала, используемых для определения целевого значения, и скоростью обучения.
• Преобразование целевого вектора для обучения работе с ним нейронной сети.
• Обучение нейронной сети работе с заданным целевым вектором и получение результатов обучения.
• Преобразование векторов, содержащих результат (сигнал, сформированный сетью, и расхождение его с оригиналом) к виду удобному для анализа.
• Определение моды в векторе ошибок и сохранение её для анализа.

Количество повторений перечня действий, описанного выше, определялось пределами диапазона для поиска коэффициента скорости обучения и шагом перемещения по диапазону.

Далее в функции определялось то значение скорости обучения сети, при котором мода вектора ошибок принимала величину, минимальную по модулю, что, в свою очередь, свидетельствует о наиболее точных результатах работы сети. Полученный таким образом коэффициент скорости обучения и возвращался как результат работы рассмотренной функции.

Определение оптимального количества значений входного сигнала, используемых для определения целевого значения

Для того чтобы установить оптимальное количество входных значений, требуемое для точного определения целевого сигнала нейронной сети, была проведена серия соответствующих экспериментов. В ходе экспериментов осуществлялась оценка зависимости величины рассогласования сигнала, формируемого сетью и исходного, от количества идущих подряд входных значений, используемых для предсказания целевого.

Исследование выполнялось на примере первых трех массивов данных из одного файла одного набора измерений. Большее количество массивов данных использовать для эксперимента было нецелесообразно в силу, возникающего в этом случае, избыточного количества графической информации. Кроме того, избыточное количество массивов данных не окажет существенного влияния на точность результатов, т.к. каждая сеть настраивается для работы с конкретным массивом данных индивидуально.

Для выявления зависимости точности работы сети от количества используемых значений входного сигнала посредством соответствующей функции выполнялась следующая последовательность действий:

• создание нейронных сетей с постепенным увеличением количества значений входного сигнала, используемых для предсказания целевого;
• обучение каждой из сетей на одних и тех же массивах данных;
• моделирование работы созданных сетей с этими данными;
• выявления того значения количества входных значений, при котором мода вектора ошибок принимала величину, минимальную по модулю.

Здесь необходимо дополнительно пояснить, что от эксперимента к эксперименту количество входных значений, используемых для предсказания целевого увеличивалось на 1. Максимальное величина для данного показателя первоначально была взята равной 10. В дальнейшем предполагалось увеличить значение данного параметра, но как показали результаты анализа настройки и работы нейронных сетей, этого значения оказалось достаточно.

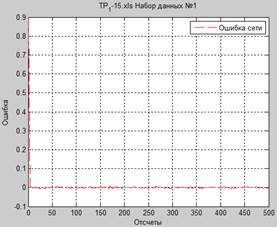
При сравнительном анализе графического представления результатов работы сети, часть из которых представлена ниже на рисунках 6, 7 и 8, существенных ошибок в работе сети при увеличении исследуемого параметра не наблюдалось. Вместе с тем с увеличением количества значений входного сигнала, используемых для предсказания целевого, происходит смещение точки начала аппроксимации сетью обрабатываемого набора данных.

а                                                                 б

в                                                                 г

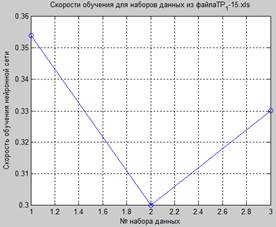
Рисунок 6. Результаты и характеристики работы сети (для 5 значений):

а – исходный и сформированный сигналы, б – отклонение сформированного сигнала от исходного, в – скорость обучения сети (для 3 массивов данных), г – весовые коэффициенты (для 3 массивов данных)

а                                                                б

в                                                                 г

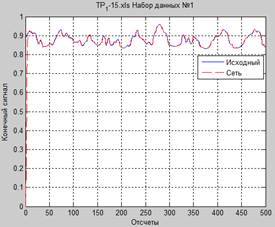
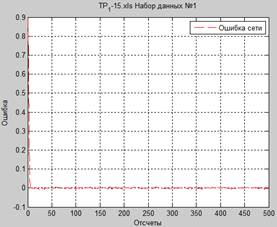
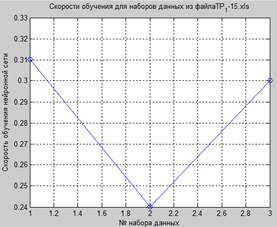
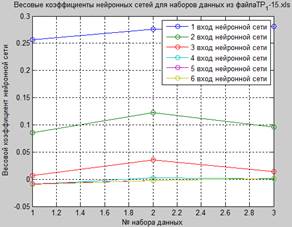
Рисунок 7. Результаты и характеристики работы сети (для 6 значений):

а – исходный и сформированный сигналы, б – отклонение сформированного сигнала от исходного, в – скорость обучения сети (для 3 массивов данных), г – весовые коэффициенты (для 3 массивов данных)

а                                                                б

в                                                                 г

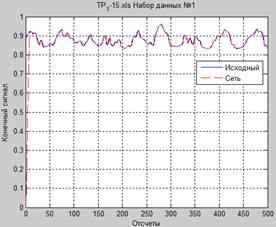
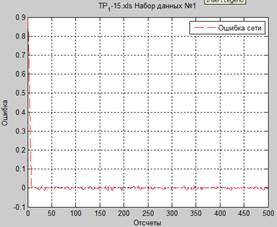
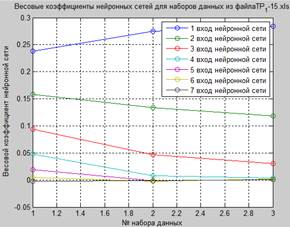
Рисунок 8. Результаты и характеристики работы сети (для 7 значений):

а – исходный и сформированный сигналы, б – отклонение сформированного сигнала от исходного, в – скорость обучения сети (для 3 массивов данных),  г – весовые коэффициенты (для 3 массивов данных)

Для каждого набора данных на протяжении большинства экспериментов с ростом количества значений исходного сигнала, используемых для определения целевого значения нейронной сетью, наблюдается снижение оптимальной скорости обучения сети, т.е. скорости с которой сети обучается быстрее всего и с минимальным значением величины ошибки. Скорость обучения и статистические показатели отклонения сигнала сети от целевого по рассматриваемым экспериментам приведены в таблицах 2, 3 и 4, а средние значения показателей – в таблице 5. Максимальные и минимальные значения параметров выделены жирным и подчеркнутым текстом, соответственно.

Таблица 2.

Скорость обучения и статистические показатели отклонения сигнала сети от целевого для массива данных №1

Таблица 3.

Скорость обучения и статистические показатели отклонения сигнала сети от целевого для массива данных №2

Таблица 4.

Скорость обучения и статистические показатели отклонения сигнала сети от целевого для массива данных №3

Таблица 5.

Средние значения скорости обучения и статистических показателей отклонения сформированного сигнала от исходного для данных из таблиц 2, 3, 4

Проанализировав значения, представленные в таблицах 2 – 5, можно сделать следующие выводы о работе сетей в случае каждого из массивов данных:

1. Набор №1

• Стабильное увеличение минимального порогового значения ошибки происходит на протяжении первых 5 экспериментов. Аномальное снижение наблюдается в 7 эксперименте. 
• Максимальное значение ошибки одинаково для всех экспериментов. Данное значение ошибки соответствует самому первому отсчету в наборе данных, что подтверждается соответствующими графиками.
• Среднее значение и стандартное отклонение значений ошибки в работе нейронной сети устойчиво увеличиваются от эксперимента к эксперименту, за исключением аномально резкого возрастания в 7 эксперименте.

2. Набор №2

• Стабильное увеличение минимального порогового значения ошибки происходит на протяжении первых 4 экспериментов.
• Максимальное значение ошибки одинаково для всех экспериментов. Данное значение ошибки соответствует самому первому отсчету в наборе данных, что подтверждается соответствующими графиками.
• Среднее значение и стандартное отклонение значений ошибки в работе нейронной сети устойчиво увеличиваются от эксперимента к эксперименту, за исключением аномально резкого возрастания в 9 эксперименте. В данном серии экспериментов сохраняется та же тенденция, что и для набора №1.

3. Набор №3

• Стабильное увеличение минимального порогового значения ошибки происходит на протяжении первых 5 экспериментов. Резкое снижение наблюдается в 9 эксперименте.
• Максимальное значение ошибки одинаково для всех экспериментов. Данное значение ошибки соответствует самому первому отсчету в наборе данных, что подтверждается соответствующими графиками.
• Среднее значение и стандартное отклонение значений ошибки в работе нейронной сети устойчиво увеличиваются от эксперимента к эксперименту, за исключением резкого возрастания в 9 эксперименте. В данной серии экспериментов сохраняется та же тенденция, что и в первых двух случаях.

В ходе проведения исследований были также определены средние значения параметров нейронной сети (скорость обучения и количество входных значений), допустимых при построении модели, описывающей тремор кистей рук. Вместе с тем их применение не гарантирует максимально точного соответствия модели исходным данным. Описанная ситуация возникает из-за того, что нейронная сеть для корректной работы в каждом конкретном случае требует, как правило, достаточно точной настройки по упомянутым параметрам и большого количества итераций обучения.

Заключение

Таким образом, обобщая результаты экспериментов, выполненных в рамках данной работы, для каждого из наборов данных, можно сделать вывод, что нейронная сеть типа Adaline позволяет получить математическую модель треморограмм высокой степени точности. Для работы с имеющимися наборами данных оптимальные значения таких ключевых параметров нейронной сети типа Adaline, как количество входных значений, используемых для предсказания целевого и скорость обучения сети в каждом конкретном случае оказались различны. По этой причине для обеспечения максимально возможной точности соответствия результата работы нейронной сети целевому вектору моделируемого сигнала упомянутые выше параметры следует подбирать индивидуально с помощью разработанных функций. В качестве опорного показателя при подборе следует использовать моду вектора ошибок сигнала сети. Соответственно, минимум указанного параметра будет являться критерием останова процесса подбора величин коэффициента скорости и количества входных значений для предсказания целевого сигнала.