МЕХАНИЧЕСКАЯ ТЕОРИЯ ДВИГАТЕЛЯ ОТТО: ВЫВОД ОСНОВНЫХ УРАВНЕНИЙ В ПЕРВОМ ПРИБЛИЖЕНИИ

 

THE MECHANICAL THEORY OF OTTO ENGINE: DERIVATION BASIC EQUATIONS IN FIRST APPROXIMATION

 

Nodir Kodirov

Independent researcher, Uzbekistan

 

Аннотация. Согласно устоявшимся научным представлениям, двигатель Отто является тепловой машиной. В статье, исходя из механики Ньютона, двигатель Отто рассматривается как механическая машина, подвод теплоты к рабочему телу которой является частным случаем подведения энергии. Даны определения коэффициенту полезного действия и выведено уравнение для его вычисления.

Abstract. According to well-established scientific concepts, Otto's engine is a heat engine. In the article, based on Newtonian mechanics, the Otto engine is considered as a mechanical machine, the supply of heat to the working fluid of which is a special case of supplying energy. The definitions of the efficiency are given and the equation for its calculation is derived.

 

Ключевые слова: Двигатель Отто, четырехтактный двигатель, теплота, коэффициент полезного действия, “Механическая теория двигателя Отто”.

Keywords: Otto engine, four-stroke engine, heat, effieciency, “The mechanical theory of Otto engine”.

 

1. Предпосылки к созданию механической теории двигателя Отто

Двигателем Отто называется четырехтактный поршневой двигатель внутреннего сгорания с внешним смесеобразованием и принудительным (искровым) зажиганием, основой конструкции которого является центральный кривошипно-шатунный механизм (далее КШМ).

Описание работы двигателя Отто имеется в любом учебнике по традиционной теории поршневых двигателей и поэтому не приводится.

 

 

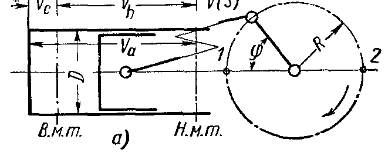
Рисунок 1. Схематичное изображение двигателя Отто [5, с. 62]

 

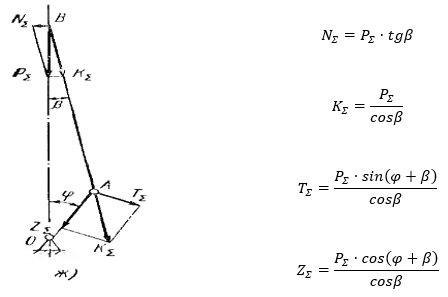
Рисунок 2. Схема действующих в КШМ сил [5, с.302]

 

где P_Σ-суммарная сила на поршне, N_Σ-боковая сила, К_Σ-продольная сила, T_Σ-тангенциальная сила, Z_Σ-радиальная сила, φ-угол поворота коленчатого вала, β-угол отклонения шатуна.

Из табл. VIII [2, с. 546] следует, что тангенциальная сила T_Σ при некоторых положениях механизма может по величине превысить суммарную силу P_Σ, что объясняется справедливостью «золотого правила» механики применительно к КШМ: «выигрываешь в силе-проигрываешь в расстоянии, выигрываешь в расстоянии-проигрываешь с силе».

В некотором диапазоне углов поворота коленчатого вала поршень проходит расстояние большее, чем путь, проходимый осью шатунной шейки коленчатого вала, именно в этом диапазоне тангенциальная сила на коленчатом валу и превышает по величине суммарную силу на поршне.

Но если «золотое правило» механики справедливо для некоторого диапазона положений КШМ, то справедлив будет и рассматриваемый ниже идеальный двигатель Отто.

2. Идеальный двигатель Отто. Положительная, отрицательная и полезная работа на коленчатом валу. Вывод формулы термического коэффициента полезного действия (далее КПД на коленчатом валу) на коленчатом валу

Допущения к рассмотрению идеального двигателя Отто:

- нет никакого трения и иных потерь;

- всякая сила считается постоянной по величине;

-коленчатый вал вращается равномерно;

-в такте расширение поршень является ведущим звеном КШМ, а в тактах выпуск, впуск и сжатие ведущим звеном КШМ является коленчатый вал.

Первый такт расширение. К поршню, находящемуся в верхней мертвой точке (далее: ВМТ), подводится энергия Q (необязательно тепловая, это может быть и механический импульс), эквивалентная работе:

где 4-количество ходов в рабочем цикле, S-ход поршня,

где R-радиус коленчатого вала. В результате поршень за счет работы силы перемещается к нижней мертвой точке (далее: НМТ) на расстояние:

 под действием силы, на что затрачивается работа:

 

от всей подведенной энергии Q. За этот ход сила на поршне поворачивает коленчатый вал на угол π, действуя на него с силой Т, что приводит к перемещению шатунной шейки на расстояние:

на что затрачивается работа:

Согласно «золотому правилу» механики, сила Т равна:

Остаток подведенной энергии Q, равный:

запасается в коленчатый вал (для простоты), что выражается некоторой силой:

Далее в трех ходах уже коленчатый вал с силой Т перемещает поршень на расстояние:

Сила Т₃ равномерно распределяется по трем тактам, отсюда:

Однако, согласно определению из элементарной физики, работа силы положительна, если она ускоряет тело, и отрицательна, если оно замедляет его [4, с. 185].

Известно, что в КШМ в первой половине хода до определенного угла ПКВ всегда поршень ускоряется, во второй половине же хода поршень замедляется. Если вычислить угол ПКВ, когда скорость поршня максимальна, то можно точно вычислить всю положительную и отрицательную работу силы на коленчатом валу, соответственно, можно вывести уравнение зависимости КПД на коленчатом валу от этого угла.

Определение 1: положительная работа силы на коленчатом валу есть работа, затрачиваемая коленчатым валом на ускорение поршня.

Определение 2: отрицательная работа силы на коленчатом валу есть работа, затрачиваемая коленчатым валом на замедление поршня.

Определение 3: полезная работа силы на коленчатом валу есть сумма по знаку положительной и отрицательной работы на коленчатом валу.

Определение 4: термический КПД на коленчатом валу есть отношение полезной работы силы на коленчатом валу к работе силы над поршнем на его перемещение во всех четырех тактах.

Некоторое отступление: если при ускорении поршня работа положительна, а при замедлении отрицательна, то можно ли говорить, что в такте расширение поршень во второй половине такта совершает отрицательную работу? Нельзя, поскольку сила на поршне в этом такте не препятствует перемещению поршня.

Обозначим угол поворота коленчатого вала, на котором скорость поршня максимальна, φ_vmax. Исходя из особенности КШМ, что максимально возможный искомый угол не может быть больше 90 град или , а при  ускорения поршня быть не может, область определения искомого угла .

Используя особенность КШМ, заключающуюся в том, что в первой половине такта до определенного угла поворота коленчатого вала поршень ускоряется-тогда работа положительна, во второй половине же такта поршень замедляется-тогда работа отрицательна. Известно, что искомый угол ПКВ находится после ВМТ в тактах расширение-впуск и до ВМТ в тактах выпуск-сжатие. Такт расширение из решения исключается, так как работа на всем протяжении такта положительна. Остаются такты выпуск, впуск и сжатие.

ВЫВОД:

1. В такте расширение вся работа силы на коленчатом валу положительна:

2. Такт выпуск. Особенностью КШМ является то, что угол ПКВ, на котором скорость поршня максимальна, равен не φmax, а , поскольку в тактах впуск и расширение поршень движется от ВМТ к НМТ, а в тактах сжатие и выпуск от НМТ к ВМТ.

Полная работа силы на коленчатом валу:

Так как, угол φmax в такте выпуск-сжатие находится до ВМТ, то положительная работа силы на коленчатом валу:

Соответственно, отрицательная работа силы на коленчатом валу:

Полезная работа в такте:

=

=

Так как:

То:

=

=

3. Такт впуск. Полная работа силы на коленчатом валу в такте впуск:

Положительная работа силы на коленчатом валу:

Отрицательная работа силы на коленчатом валу:

Полезная работа силы на коленчатом валу:

=

=

Так как:

То:

=

=

4. Такт сжатие. Результат такой же, как и для такта выпуск:

Tак как положительная работа в такте расширение:

То полезная работа в цикле

+

+=

=

Термический КПД на коленчатом валу:

  

                                                                                                   (1)

Последовательность рабочего цикла идеального двигателя Отто ясна из описания выше- расширение-выпуск-впуск-сжатие. Необходимо подчеркнуть, что полученная не учитывает механические потери, имеющие место быть в реальных двигателях.

3. Нахождение угла поворота коленчатого вала, на котором скорость поршня максимальна

Чтобы найти угол ПКВ φvmax, на котором скорость максимальна, достаточно решить уравнение 309 [5, с. 295]:

,

где λ- отношение радиуса кривошипа (коленчатого вала) к длине шатуна,

 

Решение:

Так как:

То:

Далее:

Обозначим:

Получаем квадратное уравнение:

Из квадратного уравнения выше:

Решаем и получаем два корня:

Численная проверка показала, что действительный корень только один:

Теперь:

И действительный корень уравнения:

                                                                                                   (2)

4. Применение выдвигаемой теории к реальным двигателям

Согласно термодинамики, термический КПД идеального цикла Отто не зависит ни от механики, ни от степени повышения давления, а зависит только от степени сжатия и свойства рабочего тела (показателя адиабаты k) [3, с. 239]:

                                                                                                              (3)

Определение 5: термический КПД поршня идеального двигателя Отто есть отношение работы силы над поршнем во всех четырех тактах ко всей подведенной теплоте:

                                                                                                                   (4)

Определение 6: Общий КПД идеального двигателя Отто есть произведение термического КПД поршня и термического КПД на коленчатом валу и выражает отношение работы силы на коленчатом валу во всех четырех тактах ко всей подведенной теплоте:

                                                                                              (5)

Приняв, что термический КПД идеального цикла Отто и термический КПД поршня идеального двигателя Отто суть одно и тоже, а также исходя из того, что сила на поршне есть произведение давления на площадь поршня, в табл. 1 приведен общий КПД идеального двигателя Отто применительно к реальным двигателям. Уравнение:

Таблица 1.

Общий КПД (без учета механических потерь) некоторых реальных двигателей (λ из разных источников)

№	Марка, модель	λ	ηс	ε	ηр	ηО
1.	ВАЗ-21124	0,293	0,291	10,30	0,607	0,177
2.	ВАЗ-21126	0,284	0,290	11,00	0,617	0,179
3.	ВАЗ-21129	0,284	0,290	10,45	0,609	0,177
4.	ВАЗ-21179	0,336	0,296	10,30	0,607	0,180
5.	ВАЗ-11182	0,295	0,291	10,50	0,610	0,177
6.	Honda Integra Type R	0,316	0,294	11,00	0,617	0,181

 

Так как производители легковых автомобилей не указывают эффективный удельный расход топлива, единственным достоверным источником, дающим возможность выяснить значение КПД хотя бы одного реального двигателя, является приложение 5 [1, с.88-89]. Выбираем самый неэкономичный двигатель МеМЗ-966 с эффективным удельным расходом топлива на номинальной частоте вращения коленчатого вала:

,

 Что в переводе в единицы измерения СИ составляет:

.

Вычислить же реальный общий КПД можно по уравнению [5, с.157]:

В нашем конкретном случае это:

или 20%.

Но ведь это двигатель, выпускавшийся в 70-х годах прошлого века в бывшем СССР, и даже у него с учетом механических потерь общий (в данном случае эффективный) КПД выше, чем у любого из современных двигателей без учета механических потерь, приведенных в табл.1, чего в принципе не может быть. Другими словами, термический КПД идеального цикла Отто и термический КПД поршня идеального двигателя Отто по сути разные величины.

5. Термический КПД поршня идеального двигателя Отто

Как уже сказано выше, согласно термодинамики, термический КПД идеального цикла Отто не зависит ни от механики, ни от степени повышения давления, а зависит только от степени сжатия и свойства рабочего тела (показателя адиабаты k) [3, стр. 239]:

 

 

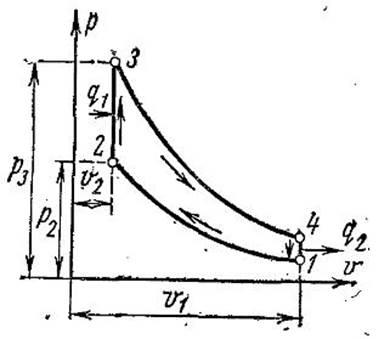
Рисунок 3. p-V-диаграмма идеального цикла Отто [3, с. 238]

 

 

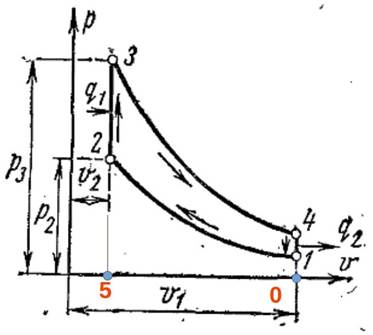
Рисунок 4. (отредактированный рис. 3)

 

 

Рисунок 5. T-S-диаграмма идеального цикла Отто [3, с. 238]

 

На p-V диаграмме (Рис.3) площадь фигуры 1-2-3-4 есть не что иное, как разность работы расширения и сжатия:

или площадь фигуры 0-5-3-4 за вычетом площади фигуры 0-5-2-1 (Рис.4), причем выражение:

есть преобразованная в механическую работу теплота, являющаяся разницей площадей фигур 6-2-3-5 и 6-1-4-5 на T-S диаграмме (Рис. 5) и соответствует площади фигуры 1-2-3-4 на p-V диаграмме (Рис.3).

Другими словами, возвращаясь к идеальному циклу Отто, теоретическая полезная работа идеального двигателя Отто выражается не разницей, а суммой площадей двух фигур: 0-5-3-4 и 0-5-2-1 (Рис.4).

Выведем формулу термического КПД поршня идеального двигателя Отто преобразованием уравнения теоретической полезной работы [3, стр. 240], но сначала нужно выяснить, можно ли получить это уравнение преобразованием располагаемых внешних (полезных) работ двух изохорных процессов 2-3 и 4-1 (Рис.3).

Располагаемая внешняя (полезная) работа изохорного процесса (Рис.3) 2-3 [1, с.80]:

Располагаемая внешняя (полезная) работа изохорного процесса (Рис.3) 4-1 [1, с.80]:

Вычитаем второе от первого и получаем:

Раскрываем скобки:

Последнее уравнение описывает фигуры 3-4-0-5 и 1-2-5-0 (рис.4), выражающие работу адиабатного расширения l_e и адиабатного сжатия l_c идеального цикла Отто. Уравнение работы изменения объема согласно определению [1, с.85] дополняется выражением :

Если уравнение теоретической полезной работы [3, стр. 240] можно получить преобразованием разницы располагаемых внешних (полезных) работ двух изохорных процессов с прибавлением выражения выше, то сумму тех же располагаемых внешних (полезных) работ двух изохорных процессов можно получить обратным приемом, удалив дополняющее выражение :

Раскрываем скобки:

Получаем:

И:

В итоге сумма фигур 3-4-0-5 и 1-2-5-0 (рис.4), выражающих работу адиабатного расширения l_e и адиабатного сжатия l_c идеального цикла Отто, описываются как разница располагаемых внешних (полезных) работ двух необычныx изохорных процессов.

Теплота процессa:

равна:

Теплота процесса:

равна:

Тогда сумма располагаемых внешних (полезных) работ двух необычных изохорных процессов 2-3 и 4-1 выражается в теплоте уравнением:

Действия выше не более чем математический приём для вычисления суммы площадей фигур 0-5-3-4 и 0-5-2-1.

Подводимая теплота q₁ неизменна:

или площадь фигуры 3-5-6-2 на T-S диаграмме (Рис.5)

Параметры характерных точек известны [3, с.238]:

, , ,

,

где k- показатель адиабаты, Λ-степень повышения давления.

Термический КПД поршня идеального двигателя Отто:

==

=

Окончательно:

                                                                                                        (6)

В идеальном двигателе Отто расширение и сжатие совершаются по адиабате k=1,4. Для расчета реальных двигателей показатель политропы n₄ вычисляется по уравнению:

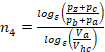
а лучше по этому:

где ε- степень сжатия, V_a- полный объем цилиндра, V_hc- объём камеры сгорания. Так как:

 

A:

То уравнения выше приводятся к виду:

                                                                                                             (7)

И:

                                                                                                            (8)

6. Дополнение уравнения термического КПД поршня

Выведенное уравнение (6) термического КПД поршня, строго говоря, неполное, поскольку не учитывает работу силы над поршнем в тактах выпуск и впуск. В термодинамике подразумевается, что эти два такта есть изобарные процессы [3, стр. 237]. На рис. 6 приведено изображение тактов выпуск (отрезок 1-6) и впуск (отрезок 6-1) на p-V-диаграмме.

 

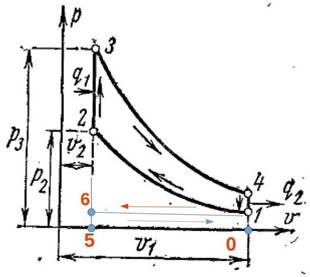
Рисунок 6. Изображение тактов выпуск и впуск на p-V диаграмме

 

Располагаемая внешняя (полезная работа) в изобарном процессе равна нулю [3, с.82], но удельная работа изменения объёма имеет смысл [3, с.82]:

Однако оба этих такта, в действительности, не являются строго изобарными. Для дополнения выведенного уравнения (6) термического КПД поршня, предлагается вычислить дважды площадь фигуры 6-1-0-5 для тактов выпуск и впуск и прибавить к уравнению (6):

или

Kоличество теплоты в двух этих тактах:

, где Т₀- температура окружающей среды, Т₁-температура рабочего тела в конце такта впуск-начале такта сжатие.

Так как подводимая теплота q₁ неизменна:

То дополнительный член уравнения (8):

Так как:

То:

Полное уравнение термического КПД поршня принимает вид:

                                                                                   (9)

Итак, термический КПД поршня идеального двигателя Отто:

- зависит от степени сжатия и свойства рабочего тела;

-зависит от степени повышения давления.

Параметры характерных точек [3, с.238]:

p₁-p_a- давление в начале такта сжатие, Т₁-Т_а- температура в начале такта сжатие, р₂-р_с- давление в конце такта сжатие, Т₂-Т_с- температура в конце такта сжатие, р₃-p_z- давление в начале такта расширение, Т₃-Т_z- температура в начале такта расширение, p₄-p_b- давление в конце такта расширение, Т₄-T_b- температура в конце такта расширение.

Уравнение общего КПД идеального двигателя Отто (без учета механических потерь) в первом приближении:

                                                           (10)

 В табл. 2 приводятся вычисленные по уравнениям (1), (8) и (10) значения общего КПД (без учета механических потерь) применительно к показанным выше реальным двигателям на номинальной частоте вращения коленчатого вала. Показатель n₄ вычислен по уравнению (8).

Температура То принимается 293 К, атмосферное давление 101325 Па, коэффициент избытка воздуха α=1. Расчет характерных точек рабочего тела по русской классической методике теплового расчета проф.-ров В.И.Гриневецкого-Е.К.Мазинга с некоторым учетом уточненной методики проф. И.И.Вибе.

Уточнение: расчет ведется без учета некоторых важных факторов, результаты могут не совпадать с реальными параметрами приведенных в табл.2 двигателей.

Таблица 2

Общий КПД (без учета механических потерь) некоторых реальных двигателей

№	Марка, модель	λ	ηс	ε	n4	Λ	Т1	ηр	ηО
1.	ВАЗ-21124	0,293	0,291	10,30	1,287	3,820	334	0,891	0,260
2.	ВАЗ-21126	0,284	0,290	11,00	1,289	3,700	332	0,926	0,269
3.	ВАЗ-21129	0,284	0,290	10,45	1,289	3,730	334	0,912	0,265
4.	ВАЗ-21179	0,336	0,296	10,30	1,291	3,730	334	0,913	0,270
5.	ВАЗ-11182	0,295	0,291	10,50	1,287	3,800	333	0,898	0,262
6.	Honda Integra Type R	0,316	0,294	11,00	1,293	3,730	333	0,931	0,273