Совместное размещение элементов числовых рядов, удовлетворяющих арифметической прогрессии, на множестве натуральных чисел

JOINT PLACEMENT OF NUMBER SERIES ELEMENTS SATISFACING ARITHMETIC PROGRESSION ON A LOT OF NATURAL NUMBERS

Aleksey Plakhov

Academy of the Federal Guard Service of the Russian Federation, Russia, Orel

Аннотация. Рассмотрены методы совместного размещения объектов на множестве ограниченных сверху натуральных чисел при различных ограничениях. Представлен метод совместного размещения элементов числовых рядов, удовлетворяющих арифметической прогрессии на множестве натуральных чисел, свободный от недостатков, присущих известным методам.

Abstract. The methods of joint placement of objects on the set of natural numbers bounded above from above under various restrictions are considered. The method of co-placement of elements of numerical series that satisfies arithmetic progression on a set of natural numbers, free from the disadvantages inherent in known methods is presented.

Ключевые слова: канал управления; арифметическая прогрессия.

Keywords: control channel; arithmetic progression.

В ряде практически важных случаев, возникающих в задачах управления сложными организационно-техническими системами, требуется решать задачу совместного размещения объектов на множестве ограниченных сверху натуральных чисел при различных ограничениях. К таким ограничениям могут относиться ограничения в виде условий, относительно мощности подмножеств чисел, формируемых на основе арифметической прогрессии.

Выбор арифметической прогрессии в качестве математической схемы генератора элементов совместно упаковываемых подмножеств обусловлен в задачах управления возможностью компактного описания числовых рядов, образующих упаковываемые подмножества, так как при значительных объемах подмножеств это позволяет снизить требования к объемам управляющих сообщений, передаваемых и хранимых в подсистемах управления [1, с. 41].

В общем случае рассматриваемая задача является многоэкстремальной оптимизационной задачей нелинейного программирования в n-мерном пространстве и имеет экспоненциальную сложность. Известные методы размещения объектов можно разделить на два противоположных класса: динамические методы сжатия свободного пространства или методы последовательного размещения объектов. Общий прием использования динамических методов заключается в размещении объектов уменьшенного размера в область установки и предполагает моделирование динамики изменения состояния объекта в целом, что значительно затрудняет решение задачи в условиях случайного характера управляющих воздействий, связанных с размещением новых множеств. Другая группа подходов, названных методами последовательного заполнения, рассматривает системы, подготовленные путем геометрических вычислений, без моделирования динамики элементов. Это определяет актуальность метода последовательного одиночного размещения для решения задачи размещения объектов. Этот метод состоит в том, что все элементы размещаются последовательно, причем ранее размещенные считаются неподвижными, то есть их параметры размещения имеют определенные фиксированные значения. Метод полного перебора практического интереса не представляет, так как количество итераций реализующего его алгоритма равно n!n, где n – число размещаемых элементов нового упаковываемого подмножества. Сравнительная характеристика метода динамического программирования и метода ветвей и границ для n объектов дает следующие величины: n2ⁿ для динамического программирования и 1.26ⁿ для метода ветвей и границ.

Таким образом, основным недостатком существующих подходов является отсутствие учета зависимости размещаемого объекта от уже размещенных объектов, что не позволяет применить указанные методы для решения рассматриваемой задачи.

Разработан метод совместного размещения элементов числовых рядов, удовлетворяющих арифметической прогрессии на множестве натуральных чисел, свободный от недостатков, присущих известным методам.

Количество возможных вариантов расположения незанятых элементов ограниченного сверху числового ряда определяется выражением

,                                                                                                      (1)

где , 

N – длина ограниченного сверху числового ряда;

l – количество свободных элементов в числовом ряду.

Возможность описания элементов упаковываемого подмножества из числа свободных арифметической прогрессией определяется теоремой Ван дер Вардена [2, с. 35], согласно которой хотя бы одно разбиение целых чисел содержит арифметическую прогрессию.

В этом случае элементы подмножеств представляются числовыми последовательностями, определяемыми выражением

,                                                                                                        (2)

где  – первый член арифметической прогрессии (первое число ряда, являющегося арифметической прогрессией);

 – смещение чисел арифметической прогрессии;

 – номер элемента арифметической прогрессии.

На количество вариантов размещения подмножеств влияет количество элементов ряда, в которых ранее не размещены элементы других подмножеств, мощность размещаемого подмножества, а также величина  – смещения (шага) арифметической прогрессии. При значительном количестве размещаемых подмножеств может применяться подход, заключающийся в формировании арифметической прогрессии  путем конкатенации  арифметических прогрессий, каждой со смещением . В таком случае арифметическая прогрессия  описывается выражением вида

                                                                                         (3)

В этом случае они представляют собой формулу КУ с перечислением элементов, описывающих размещение на множестве натуральных чисел позиций нового подмножества, а также смещения, относительно каждого элемента формулы.

Следовательно, при разработке алгоритма размещения нового подмножества в числовом ряду необходимо на основе имеющегося массива свободных элементов ряда  выбрать  чисел таким образом, чтобы: все выбранные свободные элементы ряда были меньше длины ряда m_p<N; выбранные для размещения элементы описывались формулой минимальной размерности, то есть для  .

В общем случая при , процесс размещения подмножества в числовом ряду представляет собой выделение из имеющего множества свободных позиций такого подмножества, сумма которых в рамках каждого окна  отвечала свойствам арифметической прогрессии и описывалось линейным уравнением вида

,                                                                                                     (4)

где  – сумма k элементов n-го окна

На итоговый выбор формулы размещения влияют следующие параметры: N – количество позиций, не занятых элементами других подмножеств; М – мощность размещаемого подмножества; j – счетчик числа элементов арифметической прогрессии; k – счетчик числа элементов формулы (первого окна) арифметической прогрессию.

Обобщение описанных выше процессов позволяет сформировать общую функциональную взаимосвязь процессов, определяющих структуру разработанного метода (рисунок 1).

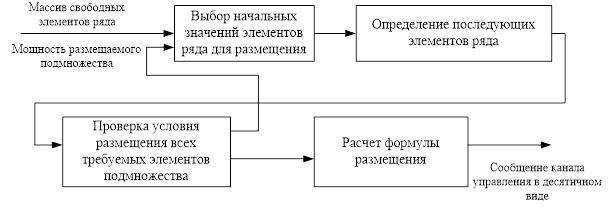
Рисунок 1.  Функциональная схема взаимосвязи процедур решения задачи размещение элементов числовых рядов, удовлетворяющих арифметической прогрессии, на множестве натуральных чисел

Известные способы выбора начальных значений (первый свободный, случайный) и объективные требования к изменяемости размещения новых подмножеств позволили сделать вывод о целесообразности случайного выбора различных чисел, определяющих арифметическую прогрессию.