Методы предварительной обработки данных ЭЭГ

Аннотация. Исходные данные записи ЭЭГ взяты из научного центра психического здоровья РАМН, которые были получены в лаборатории нейрофизиологии этого центра. Рассматривается новый метод для фильтрации сигналов ЭЭГ от артефактов на базе разложения по эмпирическим модам.

Ключевые слова: Электроэнцефалограмма, эмпирическая модовая декомпозиция, обработка электроэнцефалограмм, фурье-разложение, робастное преобразование

Предобработка сигнала проводится с целью удаления артефактов, а также нейтрализации имеющихся шумовых компонент.Артефакты по их происхождению можно разделить на две группы: физические и физиологические [1].

К физическим артефактам относятся, например, помехи от электрических полей, создаваемые устройствами передачи и эксплуатации промышленного электрического тока.

Физиологические артефакты связаны с проявлениями жизнедеятельности организма и могут иметь следующее происхождение: потенциалы, возникающие вследствие движения глаз. 

Разложение сигнала по эмпирическим модам является частью преобразования Гильберта−Хуанга и представляет собой один из современных методов частотно-временного анализа нестационарных сигналов [2].

Для корректного определения эмпирических мод и их мгновенных частот в рамках метода предлагается выполнение следующих условий:

1. Локальное среднее значение каждой эмпирической моды должно быть равно нулю.

2. Число пересечений нулевого уровня графиком каждой эмпирической моды и число локальных максимумов (или минимумов) этой моды должны совпадать или отличаться не более чем на единицу.

Процедура разложения исследуемого сигнала  по эмпирическим модам предполагает следующий алгоритм:

1.Определяется положение всех локальных максимумов и минимумов входного сигнала и значение  в этих точках.

2. С использованием значений локальных экстремумов вычисляются посредством сплайновой интерполяции верхняя и нижняя огибающие сигнала  и .

3. Расчет низкочастотной составляющей сигнала (тренда) как среднего между двумя огибающими :  

4. Разность между исходным сигналом  и средним значением огибающих  принимается за первое приближение к первой внутренней модовой функции : 

5. Для полученной функции  выполняется следующая проверка: – если отвечает двум определенным выше свойствам внутренней модовой функции, то модовая функция считается извлеченной, , заменяется разностью .

– если не отвечает двум определенным выше свойствам внутренней модовой функции, то  заменяется на , повторяются шаги 1–5, и вычисляется второе приближение к первой внутренней модовой функции 

В результате декомпозиции сигнал  может быть записан следующим образом: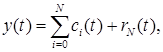 

где   – число внутренних мод;  - окончательный остаток;   – внутренние моды, ортогональные друг другу.

Разложения по первым пяти эмпирическим модам проиллюстрировано на рисунке, также данный рисунок содержит отфильтрованный сигнал.

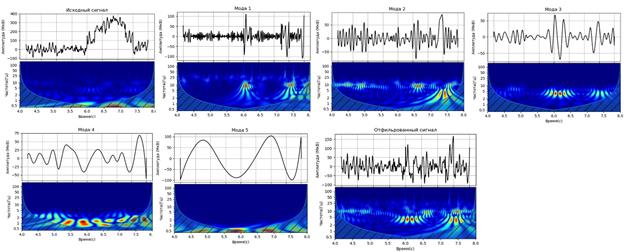
Рисунок. Пример разложения по эмпирическим мода

Описанный выше метод эмпирической модовой декомпозиции представляется перспективным для проблем, связанных с нестационарностью и нелинейностью сигналов, например, в случаях, когда сигнал не может быть адекватно представлен совокупностью гармонических функций.