Применение теории вероятности и математической статистики в экономике

APPLICATION OF THE THEORY OF PROBABILITY AND MATHEMATICAL STATISTICS IN ECONOMY

Angelina Zhivoglazova

Student, Socio-economic Institute SSTU named after Gagarina Yu. A., Russia, Saratov

Аннотация. Статья посвящена вопросам практического применения теории вероятности и математической статистики к экономическим вопросам. В статье рассмотрены основные понятия теории вероятности: событие, вероятность, случайные величины и закон их распределения. Представленные примеры решения задач демонстрируют использование инструментов теории вероятности и статистики для различных отраслей экономики.

Abstract. The article is devoted to the issues of practical application of the theory of probability and mathematical statistics to economic issues. The article discusses the basic concepts of the theory of probability: event, probability, random variables and their distribution law. The presented examples of problem solving demonstrate the use of tools of the theory of probability and statistics for various sectors of the economy.

Ключевые слова: Событие, теория вероятностей, математическая статистика, вероятность события, формула Бернулли, неравенство Маркова, математическое ожидание.

Keywords: Event, probability theory, mathematical statistics, event probability, Bernoulli formula, Markov inequality, mathematical expectation.

В современном мире в связи с растущими потребностями населения возникает необходимость расширения рынка товаров и услуг, что, в свою очередь, обуславливает развитие экономики в целом.

Экономика- это наука, которая изучает, как люди используют имеющиеся ограниченные ресурсы для удовлетворения своих неограниченных потребностей в жизненных благах [1].

Между тем, экономика, несмотря на длительное свое существование, не способна прогнозировать изменения, происходящие в обществе. В этих ситуациях безусловным подспорьем является использование методов эконометрики, в частности, теории вероятности и математической статистики.

Правила теории вероятности и математической статистики распространяется на весь финансовый рынок, поскольку его деятельность не является закономерной, ее результаты довольно сложно просчитать и предугадать, однако это возможно сделать, если выразить данные финансовые события через призму терминов моделей вероятностно- статистического анализа [2].

Использование вероятностной модели позволяет трансформировать реальные экономические события в математическую схему статистических данных, которая позволит произвести вычисления и получить конкретный результат.

Таким образом, теория вероятности и математическая статистика позволяет учесть факторы, способные влиять на явления и события, исход которых предсказать сложно.

Вероятность Р появления события оценивается в диапазоне от 0 до 1, причем при Р=0 появление события считается невозможным, а при Р=1- достоверным, произошедшим в любом случае при данных условиях.

В свою очередь, события делятся на независимые, не влияющие друг на друга, и зависимые, в случае, когда их наступление взаимосвязано.

Рассмотрим задачу с независимыми событиями: в городском соревновании по строительству за получение гранта борются две строительные компании. Вероятность победы первой компании равна 0,8, а вероятность победы второй- 0,7. Найти вероятность того, что грант получит только одна компания.

Решение:

Введем обозначения: А- событие, заключающееся в том, что победила 1 компания; В- событие, заключающееся в том, что победила 2 компания; А₁- событие, при котором 1 компания победила, а вторая - проиграла; В₂- событие, при котором2 компания победила, а первая-проиграла.

Р(А)= 0,8

Р(В)= 0,7

Р(А₁) = Р(А)∙(1-Р(В)) = 0,8∙0,3 =0,24

Р(В₁) =Р(В)∙(1-Р(А)) = 0,7∙0,2= 0,14 

Искомая вероятность события определяется как сумма вероятностей Р(А₁) и Р(В₁).

Р(А₁+В₁) = 0,24+0,14= 0,38

Ответ: 0,38

В экономических задачах не редко используется схема независимых испытаний, вероятность выпадения которых одинакова и не зависит от количества повторов.

Для решения таких задач используется формула Бернулли [3]:

, где q=1-p

- вероятность того, что событие А наступит m раз при n независимых испытаниях.

Рассмотрим задачу: каждый пятый клиент банка осуществляет полное снятие вложенной суммы со своего счета. Какова вероятность, что трое клиентов снимут вложенную сумму, если в банке находятся 7 человек.

Решение:

Введем обозначения:  n= 7;   m=3;   р=;   q=1-р=1-= 

Тогда,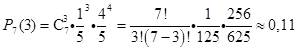 

Ответ: Р

Для решения задач отклонения определенной величины от ее среднего значения используют неравенство Маркова [4]:

, где М(х)- математическое ожидание.

Задача: Оценить среднюю сумму денег, которую клиент снимает с банкомата при условии, что вероятность снятия 10000 рублей менее 0,4.

Решение:

Введем обозначения: α=10000, р=0,4

Полагая, что М(х)=р∙α, получим: М(х)=10000∙0,4=4000

Ответ: средняя сумма денег, снимаемая в банкомате, составляет 4000 рублей.

Рассмотренные решения экономических задач демонстрируют тесное переплетение экономики и математических наук, в частности теории вероятностей и математической статистики.