Современные требования к уроку математики
Журнал: Научный журнал «Студенческий форум» выпуск №42(135)
Рубрика: Физико-математические науки

Научный журнал «Студенческий форум» выпуск №42(135)
Современные требования к уроку математики
Аннотация. В статье определяется применение современных требований по ФГОС на уроках математики.
Ключевые слова: современные требования, ФГОС, цилиндр.
Современный урок математики по своему содержанию и структуре представляет весьма сложную организационную форму педагогического процесса. Сложность его обусловлена большим разнообразием тех задач и целей, которые решаются на каждом уроке в отдельности и на совокупности уроков по данной теме.
Современная жизнь предъявляет сегодня человеку жёсткие требования – это высокое качество образования, коммуникабельность, целеустремлённость, креативность, качества Лидера, а самое главное – умение ориентироваться в большом потоке информации.
В новых Стандартах сформулированы требования к сегодняшнему учителю[1]:
Во - первых, это профессионал, который
- демонстрирует универсальные и предметные способы действий;
- инициирует действия учащихся;
- консультирует и изменяет их действия;
- находит методы подключения в работу любого учащегося;
- создаёт обстоятельства для приобретения учащимися жизненного опыта.
Во - вторых, это учитель, использующий развивающие технологии.
В - третьих, современный учитель располагает информативной компетентностью.
Требования к современному уроку [2]:
- Подобранный урок в отлично оборудованном кабинете вынужден иметь хорошее начало и хорошее окончание;
- Учитель обязан запланировать свою деятельность и деятельность учащихся, отчетливо сконструировать тему, цель, задачи урока;
- Урок должен являться проблематичным и развивающим: преподаватель сам нацеливается на сотрудничество с учащимися и умеет направлять учащихся на сотрудничество с преподавателем и одноклассниками;
- Учитель организует проблематичные и поисковые ситуации, вызывает деятельность учащихся;
- Вывод осуществляют сами учащиеся;
- Минимум репродукции и максимум творчества и сотворчества;
- Время сбережение и здоровье сбережение;
- В центре внимания урока - дети;
- Учет степени и возможностей учащихся, в котором предусмотрены такие аспекты, как профиль класса, тяга учащихся, настроение детей;
- Умение показывать методическое искусство учителя;
- Планирование обратной связи;
- Урок должен быть добрым.
Необходимо обратить внимание и на принципы педагогической техники:
1. Свобода выбора (в каждом обучающем или управляющем деянии учащемуся
предоставляется право выбора);
2. Открытости (не исключино давать знания, однако и показывать их границы, сталкивать учащегося с проблемами, ответы которых лежат за пределами исследуемого курса);
3. Деятельности (освоение учениками знаний, умений, навыков преимущественно в форме деятельности, ученик должен уметь использовать свои знания);
4. Идеальности (максимально извлекать возможности, знания, интересы самих учеников );
5. Обратной связи (регулярно контролировать процесс преподавания с помощью развитой системы приемов обратной связи).
Реализация этой точки зрения присутствует в следующем уроке.
Конспект урока по геометрии в 11 классе по теме «Цилиндр»
Тип урока: открытие новых знаний
Цели урока:
1. Сформировать у учащихся знания о теле вращения – цилиндр (определение, элементы цилиндра, сечение цилиндра, формулы площади боковой и полной поверхности цилиндра);
2. Продолжить формирование логических и графических умений;
3. Развитие познавательного интереса через творческую активность, исследовательскую деятельность на основе умения делать обобщения по данным, полученным в результате исследования.
4. Развивать пространственные представления на примере тела вращения.
Задачи урока:
1. Познакомить учащихся с новым видом тела вращения – цилиндром;
2. Сформировать умение решать задачи на нахождение элементов цилиндра;
3. Расширить знания о геометрии.
4. Воспитание ответственного отношения к учебному труду, воли и настойчивости для достижения конечных результатов при изучении темы;
5. Воспитание интереса к математике, как науки.
6. Развитие навыков самоконтроля;
Ход урока
1. Организационный момент
Приветствие обучающихся. Проверка готовности к уроку.
2. Актуализация знаний
С этим геометрическим телом человек знаком давно. Этому способствовали виды стволов деревьев, из которых со временем начали изготавливать балки для строительства жилищ, мостов и других сооружений. Ещё 3–4 тысячи лет назад люди научились украшать храмы и дворцы высокими колоннами, для чего из каменных глыб вытёсывали это. Древний термин названия этого происходит от греческого слова “килиндро” – вращаю, катаю. “Килиндрос” – свиток, валик. Евклид, указывая на способ образования этого, говорит, что если прямоугольник, вращающийся около одной из сторон, снова вернётся в то же самое положение, из которого он начал двигаться, то описанная фигура и будет этим геометрическим телом.
Как вы думаете, о чём идёт речь?
(Учащиеся предлагают варианты ответов)
Вот и поговорим сегодня о геометрическом теле, о цилиндре.
3. Изучение нового материала
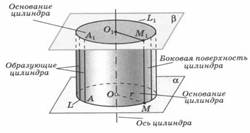
Рисунок 1. Цилиндр
Рассмотрим две параллельные плоскости α и β и окружность L с центром О радиуса r, расположенную в плоскости α. (рисунок на доске). Через каждую точку окружности L проведем прямую, перпендикулярную к плоскости α. Отрезки этих прямых, заключенные между плоскостями α и β, образуют цилиндрическую поверхность.
Сами отрезки называются образующими цилиндрической поверхности.
Тело, ограниченное цилиндрической поверхностью и двумя кругами с границами L и ![]() , называется цилиндром.
, называется цилиндром.
Цилиндрическая поверхность называется боковой поверхностью цилиндра, а круги – основанием цилиндра.
Образующие цилиндрической поверхности называются образующими цилиндра, прямая ![]() – осью цилиндра.
– осью цилиндра.
Длина образующей называется высотой цилиндра, а радиус основания – радиусом цилиндра.
Данный рисунок перечертите себе в тетрадь правильно обозначьте все элементы цилиндра.
Цилиндр может быть получен вращением прямоугольника вокруг одной из его сторон. На рисунке изображен цилиндр, полученный вращением прямоугольника ABCD вокруг стороны AB. При этом боковая поверхность цилиндра образуется вращением стороны CD, а основания – вращением сторон BC и AD.
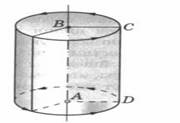
Рисунок 2. Сечение цилиндра
Рассмотрим сечения цилиндра различными плоскостями. Если секущая плоскость проходит через ось цилиндра, то сечение представляет собой прямоугольник, две стороны которого – образующие, а две другие – диаметры оснований цилиндра. Такое сечение называется осевым.
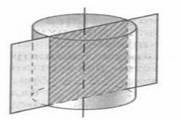
Рисунок 3. Сечение цилиндра
Если секущая плоскость перпендикулярна к оси цилиндра то сечение является кругом.
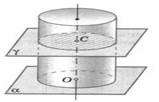
Рисунок 4. Сечение цилиндра
Данные рисунки перечертите себе в тетрадь. На практике встречаются фигуры которые имеют формы более сложных цилиндров.
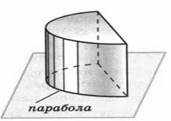
Рисунок 5. Цилиндр, в основании которого фигура, ограниченная параболой и отрезком
На рисунке изображен цилиндр, в основании которого фигура, ограниченная параболой и отрезком.
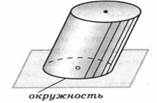
Рисунок 6. Цилиндр, у которого основания – круги, но образующие не перпендикулярны основаниям
На рисунке изображен цилиндр, у которого основания – круги, но образующие не перпендикулярны основаниям.
Но мы в курсе геометрии будем рассматривать, только такие цилиндры, которые изучили на сегодняшнем уроке, их называют прямыми круговыми цилиндрами.
На рисунке, а изображен цилиндр. Представим себе, что боковую поверхность цилиндра разрезали по образующей AB и развернули таким образом, чтобы все образующие лежали в некоторой плоскости a(рис., б). В результате в плоскости a получается прямоугольник ![]() . Этот прямоугольник называется разверткой боковой поверхности цилиндра. Основание
. Этот прямоугольник называется разверткой боковой поверхности цилиндра. Основание ![]() – развертка окружности основания, а высота AB- образующей цилиндра, поэтому
– развертка окружности основания, а высота AB- образующей цилиндра, поэтому ![]() ,
,![]() , где r – радиус цилиндра, h – высота цилиндра.
, где r – радиус цилиндра, h – высота цилиндра.
За площадь боковой поверхности цилиндра принимается площадь ее развертки.

Рисунок 7. Цилиндр, прямоугольник
Так как площадь прямоугольника ![]() равна
равна ![]() , то для вычисления площади
, то для вычисления площади ![]() боковой поверхности цилиндра радиуса r и высота h получается формула
боковой поверхности цилиндра радиуса r и высота h получается формула
![]()
Итак, площадь боковой поверхности цилиндра равна произведению длины окружности основания на высоту цилиндра.
Площадью полной поверхности цилиндра называется сумма площадей боковой поверхности и двух основания. Так как площадь каждого основания равна ![]() , то для вычисления площади
, то для вычисления площади ![]() полной поверхности цилиндра получаем формулу
полной поверхности цилиндра получаем формулу
![]()
4. Закрепление нового материала
Ученики видят список задач для классной работы. По желанию учащиеся имеют возможность решать с опережением на оценку.
№1 (523), №2 (525), №3 (527).
Самостоятельная работа
Вариант 1.
№1. Длина окружности основания цилиндра равна 3. Площадь боковой поверхности равна 6. Найдите высоту цилиндра.
№2. Высота цилиндра 16 см. На расстоянии 6 см от оси цилиндра проведено сечение. Параллельные оси цилиндра и имеющее форму квадрата. Найти радиус цилиндра.
№3 Диагональ осевого сечения цилиндра равна 8 дм и составляет с образующей угол 60°. Найдите площадь полной поверхности цилиндра.
Вариант 2.
№1. Длина окружности основания цилиндра равна 1. Площадь боковой поверхности равна 4. Найдите высоту цилиндра.
№2. Радиус основания цилиндра 10 см, ось цилиндра 6 см. Площадь сечения цилиндра плоскостью, параллельной оси цилиндра 96 см2. Найти расстояние от оси цилиндра до секущей плоскости.
№3 Диагональ осевого сечения цилиндра равна 8![]() дм и образует с плоскостью основания цилиндра угол 45°. Найдите площадь полной поверхности цилиндра.
дм и образует с плоскостью основания цилиндра угол 45°. Найдите площадь полной поверхности цилиндра.
1. Подведение итогов урока
2. Домашнее задание
Повторить стр.130-132, гл. 1, п.59-60, №530, № 537.
3. Выставление оценок за работу на уроке
4. Рефлексия учебной деятельности
Ребята давай оценим нашу работу на уроке.
Какова цель нашего урока? Достигли ли мы цели?
Продолжи фразу:
|
1. На уроке я работал 2. Своей работой на уроке я 3. За урок я 4. Материал урока мне был
5. Домашнее задание мне кажется |
активно / пассивно доволен / не доволен не устал / устал понятен / не понятен легким / трудным интересным / неинтересным |

