Клеточные автоматы и игра "Жизнь"

Клеточные автоматы – это дискретные динамические системы, поведение которых может определятся некоторым набором правил.

Клеточный автомат представляет собой равномерную и n – мерную сетку, где каждая из клеток может принимать некоторое состояние, например, 1 или 0. Время в клеточных автоматах является величиной дискретной, то есть она существует от такта к такту. В зависимости от заданного набора правил и начальных состояний, клетка на каждом такте меняет свое состояние. Правила должны одинаково применятся сразу ко всем клеткам автомата. Также правилом может регулироваться и совокупность окружающих клеток, называемых окрестностью.

Существует большое количество окрестностей, но особой популярностью пользуются два вида – окрестность Мура (r = 8) и окрестность фон Неймана (r = 4) (рисунок 1), где r – это множество клеток. 

Рисунок 1. Окрестности фон Неймана (слева) и Мура (справа)

Существует огромное количество правил перехода клеток из одного состояния в другое, следовательно, существует огромное множество различных разновидностей клеточных автоматов.

Рассмотрим одну из самых известных клеточных автоматов - игру «Жизнь», разработанную британским математиком Джоном Конвеем в 1970 году.

«Жизнь» придерживается следующих правил:

1. Каждая клетка некоторого n – мерного пространства способно находится в двух состояниях: в «живом» (заполненная) или «мертвом» (пустая).
2. Клеточный автомат использует окрестность Мура, следовательно, каждая клетка имеет 8 «соседей».
3. На каждом шаге игры, состояние всех клеток изменяется исходя из состояний его окрестностей.
4. Клетка «выживает», если соседних клеток две или три.
5. Клетка «умирает», если соседних клеток меньше двух или больше трех.
6. Клетка «рождается», если рядом находятся ровно три клетки.
7. Игра начинается, после распределения игроком «живых» клеток.

Несмотря на всю простоту правил, данный клеточный автомат способен генерировать самые разнообразные фигуры и строить сложные системы из этих фигур.

В ходе наблюдений, была разработана классификация фигур, возникающих в данном клеточном автомате:

1. Устойчивые фигуры - это фигуры, которые не изменяют свою форму.
2. Осцилляторы (периодические фигуры) – это фигуры, формы которых повторяются через некоторое количество шагов (рисунок 2).

Рисунок 2. Осциллятор пульсар

3. Двигающиеся фигуры – это фигуры, формы которых повторяются, но с некоторым смещением. Самой известной подобной фигурой является планер (рисунок 3).
4. Ружья – это фигуры, создающие движущиеся фигуры.
5. Паровозы – это двигающиеся фигуры, оставляющие за собой следы в виде фигур.

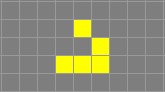
Рисунок 3. Планер (глайдер)

Существует большое количество разновидностей и модификаций данного клеточного автомата. Одним из них является «Жизнь без смерти». Особенностью данной модификации является отсутствие «смерти» клеток, то есть клетка «рождается», если рядом находятся ровно три клетки, но выживает при любом количестве соседних клеток. Данная особенность приводит к появлению уникальных структур и узоров.

Клеточные автоматы имеют широкий диапазон применения. Они используются при моделировании физических, химических и биологических процессов. Также клеточные автоматы применяются в криптографии, теории алгоритмов, теории вероятностей и статистике.