Частотная и байесовская интерпретация вероятности

Вероятность наступления некоторого события A, в классическом понимании – это отношение благоприятных исходов (m), к числу всех возможных (n) и выражается формулой (1):

Классическая интерпретация вероятности, изначально возникшая в результате анализа азартных игр, унаследовала их основную черту – равновозможность исходов. Из-за этой черты классическая вероятность имеет ограниченную область применения, так как в реальной жизни не всегда удается проверить соблюдение условия равновозможности. Еще одним недостатком является сложность представления результата испытания в виде совокупности элементарных событий. Эти проблемы решает частотная (статистическая) интерпретация вероятности. 

Частотная вероятность некоторого события A определяется через относительную частоту (W) его наступлений при большом числе испытаний и выражается формулой (2):

где m – количество реализованных событий, а n – общее число проведенных испытаний.

Частотное определение вероятности требует проведения какого-либо испытания, в отличии от основанной на умозаключениях классической вероятности. В случае проведения серии испытаний в одинаковых условиях, их относительная частота будет колебаться вокруг определенного значения. Это важное свойство называется статистической устойчивостью.

Из-за более высокой точности, в сравнении с классической вероятностью, частотную вероятность считают общепринятой и часто используют в статистике. Но несмотря на всеобщее использование, она также не лишена недостатков.

Одним из недостатков является неоднозначность результатов и их противоречивость при повторно проводимых испытаниях. Но главной проблемой частотной вероятности является невозможность его применения к единичным и уникальным событиям, так как понятие частотной вероятности относится не к конкретному событию, а к классу подобных событий.

Для решения данной проблемы была придумана байесовская интерпретация вероятности. Байесовскую интерпретацию используют тогда, когда при оценке вероятности не удается провести серию испытаний. Например, при определении вероятности уничтожения человеческой цивилизации ядерным взрывом. Вероятность этого события невозможно вычислить с помощью частотного подхода, так как подобных событий ещё не случалось.

В байесовской интерпретации, вероятность наступления события является атрибутом субъективного и неполного знания о нём, в отличии от частотной интерпретации, где вероятность – объективный атрибут мира.

В байесовском подходе выделяют два термина: априорное и апостериорное знание. Априорное знание – это знание о некотором событии, которое было получено до испытания, а апостериорное знание – это знание, следующая за испытанием. Задачей байесовского подхода является переход от априорного к апостериорному знанию, в ходе получения некоторого наблюдения. Байесовский подход выражается формулой Байеса (3):

где  – это апостериорная вероятность,  – функция правдоподобия (модель для данных), а  - априорная вероятность.

Для иллюстрации задач, решаемых байесовским подходом рассмотрим следующий пример.

Допустим, у нас имеются наблюдения за тем, какого цвета бабочку мы поймали. Обозначим их через y_i:

y₁ – желтая, y₂ – красная, y₃ – желтая.

Далее предположим следующую модель для данных:

y_i – независимы и одинаково распределены

Таблица 1.

Закон распределения

Для реализации байесовского подхода нам требуется априорное распределение на неизвестный параметр p:

Теперь нам нужно посчитать апостериорную вероятность, то есть априорную функцию плотности при условии известных y₁, y₂, y₃ 

Выразим формулу Байеса из формулы условной вероятности:

Нас интересует только зависимость от p, поэтому всё что не зависит от p будет константой:

Берем из модели вероятности и перемножаем их. Полученное выражение умножим на априорную функцию плотности. Получим:

Так как мы нашли апостериорную функцию плотности с точностью до константы, найдем константу. Для этого проинтегрируем выражение :

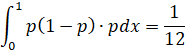
Поскольку интеграл функции плотности вероятности равен 1, помножим  на 12. Получим апостериорную функцию: