ИСТОРИЯ РАЗВИТИЯ ВЕЛИЧИН

«Геометрия происходит от слова «geo» – земля, «metria» – мерить. Геометрия – это наука о свойствах геометрических фигур. Одна из самых древнейших отраслей математики – это геометрия. Геометрические тела были известны задолго до того, как были выведены математические принципы» [1, с. 1].

Понятие величины одно из основных понятий в математике. Его смысл подвергался ряду обобщений в период развития математики.

Задатки геометрических знаний, связанных с измерением площадей, теряются в глубине тысячелетий.

Еще 4-5 тыс. лет назад вавилоняне умели определять площадь прямоугольника и трапеции в квадратных единицах. Квадрат издавна служил эталоном при измерении площадей благодаря многим своим замечательным свойствам: равные стороны, равные и прямые углы, симметричность и общее совершенство формы. Квадраты легко строить, ими можно заполнить плоскость без пробелов (в Древнем Китае мерой площади был прямоугольник).

Древние египтяне 4000 лет назад пользовались почти теми же приемами, что и мы, для измерения площади прямоугольника, треугольника и трапеции: основание треугольника делилось пополам и умножалось на высоту; для трапеции же сумма параллельных сторон делилась пополам и умножалась на высоту. Для вычисления площади S четырехугольника со сторонами а, b, с, d  применялась формула:

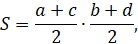
т. е. умножались полусуммы противоположных сторон. Эта формула верна только для прямоугольника. С ее помощью можно вычислить приближенно площадь таких четырехугольников, у которых углы близки к прямым.

Различные геометрические фигуры, такие как точка, прямая, кривые и ломаные, треугольники и многоугольники, встречаются в самых древних, дошедших до нас, памятниках культуры – каменных плитах, керамических сосудах, клинописных табличках, египетских папирусах.

Евклид в «Началах» даёт определения многим геометрическим понятиям, например: «Линия-длина без ширины», «Прямая линия - такая, которая одинаково расположена по отношению к своим точкам». Эти определения простейших понятий весьма расплывчаты. В современной геометрии их считают основными не подлежащими определению.

Понятие угла на протяжении веков не оставалось без изменений, оно обобщалось и расширялось под влиянием запросов практики и науки. Градусная система измерения углов, в которой за единицу принят угол, равный части угла, соответствующего полному обороту одной стороны угла около его вершины, восходит к III - II тысячелетиям до н. э., к периоду возникновения шестидесятеричной системы счисления в вавилонской математике.

Возникновение геометрии связано с различными измерительными работами, необходимыми в земледелии и строительстве, то есть с практической деятельностью людей. В дальнейшем геометрия сформировалась как самостоятельная наука – теория, которая изучает свойства геометрических фигур, не принимая во внимание другие их признаки (их природу, материал, массу, цвет и т. д.) [1, с. 1].

«В египетских папирусах и на вавилонских плитках даны задачи на определение площади треугольника. Это подтверждает, что понятия об угле и треугольнике возникли в глубокой древности и зародились они в связи с практическими потребностями, вероятно в связи со строительством примитивных жилищ. Прямой угол, связанный с образом естественно растущего растения (вертикаль) и других стоящих предметов, – одно из геометрических понятий. Даже в простейших сооружениях прямой угол выступает как самостоятельная фигура, а не элемент других фигур – прямоугольника, квадрата и пр.» [3, с. 113]

Нашим далёким предкам требовалось измерять длины не только при строительстве жилищ, но и при изготовлении различных орудий труда, а также на охоте, рыбной ловле, при обработке земли, посадке растений и пр.

Вначале для измерения длины (так же как и при счёте) люди пользовались руками, пальцами. Например, чтобы измерить длину стрелы, её сравнивали с длиной руки от локтевого сустава до конца среднего пальца, в результате появилась единица длины – локоть.

Этой единицей многие народы пользовались на протяжении тысячелетий. Расстояние, на котором надо было вбить в землю колья при постройке хижины, человек измерял шагами или длиной ступни своей ноги. Отсюда произошла единица длины, которую в одних местностях называли лапоть, в других фут [3, с. 61].

Три основные древнерусские меры длины носят названия частей тела. Меньшая мера - малая пядь - является расстоянием между раздвинутыми большим и указательным пальцами и соответствует примерно 19 см; большая пядь - расстояние между большим пальцем и мизинцем около 22-23 см (отсюда название икон, имеющих в ширину 19 или 23 см,-«пядницы»). Большая часть кирпичей ХII века имеют ширину также пядь в 19 см. Локоть есть расстояние от локтевого сочленения до концов вытянутых пальцев и соответствует двум большим пядям; и эта единица измерения имела свой вариант - локоть со сжатыми пальцами, размером в две малые пяди. Такова обычная ширина холста, чрезвычайно устойчивая и повсеместная, идущая из глубокой древности.

«Единица сажень расстояние от ступни до конца вытянутой вверх руки (примерно 215 см) при росте человека 170-172 см. Величина другого вида этой единицы измерения, так называемой простой сажени, определена историками при помощи надписи на Тмутараканском камне, содержащей сведения о промере ширины Керченского пролива. Результат этого интересного измерения «по леду от Тмутороканя до Корчева» (Керчи), произведенного в 1068 г., выразился в 14 000 сажен. Величину простой сажени определяют отсюда в 150—158 см. Она составляет расстояние между большими пальцами рук человека среднего роста, вытянутых в стороны. При последовательном делении ее на 4 и на 8 получаются известные уже нам малые локоть и пядь. По-видимому, простая сажень предшествовала обыкновенной, трехаршинной» [4, с. 13-14].

Для измерения объёмов зерна, муки и других сыпучих веществ, а также жидкостей в старину употребляли различные по размерам и названиям сосуды, причем емкость их точно не была определена.

На Руси также употреблялась мера для измерения объёмов, но применялись и другие единицы: бочка, или кадь (40 ведер), ведро. Десятую долю ведра составлял штоф, а сотую часть ведра называли чаркой.

С введением метрической системы мер за единицу жидкостей и сыпучих тел принят литр и декалитр. О более древних единицах объёма до нас сведения не дошли [3, с. 66].

«В России метрическую систему мер начали вводить с конца ХІХ в. Большая заслуга в её распространении принадлежит великому русскому химику Дмитрию Ивановичу Менделееву» [2, с. 27].

Таким образом, геометрия как наука всегда была важна для человека. За несколько наших столетий геометрия развивалась в Китае, Греции, Египте и Вавилоне. С помощью геометрии и мы сейчас изучаем задачи, для решения которых в древности потребовалось бы много сил и времени.