Математическая модель аэродромного взлета беспилотного летательного аппарата со стартовым ускорителем.

Для сокращения разбега БЛА грунтовых аэродромов предлагается использовать стартовый ускоритель на основе твердотопливного ракетного двигателя.

Для средних и тяжелых БЛА длина разбега по ВПП за счет их значительного взлетного веса может представлять достаточно большую величину порядка тысячи метров.

Кроме этого, длина разбега БЛА существенно зависит от состояния ВПП. Неудовлетворительное состояние полосы (снег, наледь, мягкий грунт и т.п.) также значительно увеличивает длину разбега БЛА.

Для резкого сокращения времени взлета, в том числе времени и длины его разбега по ВПП, можно использовать положительный опыт 60-70-х годов прошлого века, когда истребители фронтовой авиации для взлета с грунтовых аэродромов оснащались твердотопливными стартовыми ускорителями (стартовыми двигателями). Такие двигатели обеспечивали значительный прирост силы тяги и сбрасывались после выгорания их зарядов.

В существующей литературе математического описание такого вида старта нет, поэтому тема данной работы является актуальной и практически ценной для развития беспилотной технике.

В настоящее время имеется опыт использования стартовых двигателей (ускорителей) на БЛА ТУ-243 «Рейс» и БЛА «Дань-М», осуществляющих взлет с мобильных пусковых установок.

В качестве стартового ускорителя обычно используется твердотопливный стартовый двигатель (СД), подвешиваемый под фюзеляж БЛА и отбрасываемый после сгорания его заряда [1].

 Математическая модель взлета БЛА со стартовым ускорителем включает в себя 3 под модели, которые описывает следующие этапы взлета:

1.  Движение БЛА по ВПП под действием сил тяги СД и маршевого двигателя (МД) БЛА.

2.  Движение БЛА в воздухе после отрыва от ВПП при работающих СД и МД.

3.  Полет БЛА после сброса СД под действием силы тяги МД.

При моделировании движения БЛА на этих этапах будем считать его материальной точкой переменной массы m(t) и описывать движение ЦМ БЛА в вертикальной плоскости взлета в каждый момент времени t с помощью значений скорости V(t), угла наклона траектории q(t) и координат x(t), y(t) в заданной стартовой системе координат. В приведенных ниже моделях этим характеристикам присвоены индексы с номером рассматриваемого этапа взлета БЛА.

Другой особенностью предлагаемых моделей является использование в них максимального значения силы тяги МД и заданного угла атаки БЛА.

Модель движения БЛА по ВПП аэродрома

Основную роль на первом этапе взлета БЛА играет СД, который имеет тягу Р_сд и сопло, повернутое относительно строительной оси БЛА на угол j_сд. Этот угол и размещение СД выбираются таким образом, чтобы вектор силы тяги Р_сд проходил через ЦМ БЛА.

На Рис. 1 показаны составляющие силы Р_сд, которые учитываются на этапах 1 и 2 взлета БЛА.

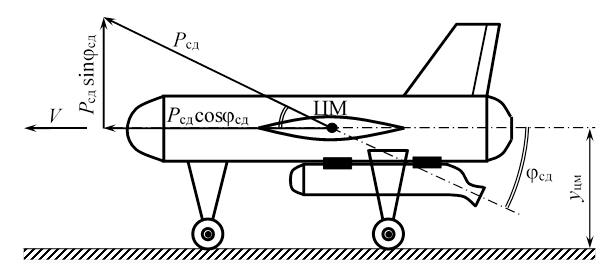
Рисунок 1.

Стартовый двигатель имеет следующие основные характеристики [1]: m_кор – масса корпуса СД (кг); m_зар – масса заряда СД (кг); m – массовая скорость горения заряда (кг/с); t – время работы СД (с).

Тогда масса объекта «БЛА+СД» будет изменяться во времени по следующему закону:

,                                                         (1)

где: т – масса БЛА.

Движение БЛА на интервале времени [0, t₁] будем описывать системой дифференциальных уравнений вида:

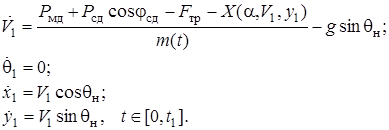                                       (2)

Здесь Р_мд – максимальное значение силы тяги маршевого двигателя БЛА (Н); х₁ = х₁(t), y₁ = y₁(t) – координаты ЦМ БЛА в момент времени t (м); F_тр = F_тр(t) – суммарное значение силы трения шасси БЛА в момент времени t(H); X(a,V₁,y₁) – сила лобового сопротивления БЛА при угле атаки a, движущегося со скоростью V₁ на высоте у₁.

Сила трения F_тр при условии, что все колеса шасси БЛА изготовлены из одного материала, вычисляется как:

F_тр = f N,                                        (3)

где: f – коэффициент трения скольжения колес шасси по ВПП (табл. 1) [2].

Таблица 1.

Из [1] следует, что N(t) = N_пер(t) + N_осн(t) реакции БЛА будет равна:

.                         (4)

Вычисляя силу тяжести как:

G(t) = m(t)g

и подставляя выражение (4) в формулу (3), получим:

,                         (5)

где: текущее значение массы m(t) вычисляется по формуле (1).

Входящая в первое уравнение системы (2) сила лобового сопротивления X(a,V₁,y₁) представляется выражением вида:

X(a,V₁,y₁) = 0,5c_x(a,V₁,y₁)r(y₁)V₁²S.                                                             (6)

Здесь c_x(a,V₁,y₁) – коэффициент лобового сопротивления при значении угла атаки БЛА, равном a (рад.); r(y₁) – плотность воздуха на высоте y₁; S – площадь крыла БЛА.

Зависимость коэффициента c_x от своих аргументов имеет вид [1]:

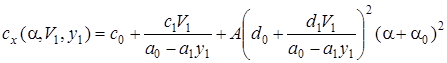,                          (7)

где: с₀, с₁, d₀, d₁, a₀, a₁ – эмпирические коэффициенты; А – коэффициент, зависящий от геометрических характеристик крыла БЛА; a₀ – балансировочный угол атаки БЛА.

В выражениях (4) и (5) через Y(a,V₂,y₂) обозначена подъемная сила БЛА, действующая при угле атаки a, при его скорости V₂ на высоте полета y₂.

Эта сила вычисляется как:

Y(a,V₂,y₂) = 0,5c_y(a,V₂,y₂)r(y₂)V₂²S.                                                             (8)

где коэффициент подъемной силы с_у определяется по следующей формуле [1]:

.                                                          (9)

Для получения зависимости плотности воздуха от высоты полета БЛА предлагается использовать следующую приближенную формулу вида [1]:

.                                                                             (10)

Здесь r₀ – плотность воздуха на уровне Земли: k – эмпирический коэффициент.

Система уравнений (2) после подстановки в нее выражений (1), (5) – (10) интегрируется на интервале времени [0, t₁] при начальных условиях:

V₁(0) = 0; q₁(0) = 0; x₁(0) = 0; y₁(0) = y_цм,                                                  (11)

где: y_цм – высота ЦМ БЛА при его предстартовом размещении на направляющих МПУ (см. Рис. 1).

Момент времени t₁ завершения этапа 1 взлета БЛА определяется из условия:

R(t₁) £ 0.                                                                                                     (12)

При достижении в процессе решения задачи (2), (11) условия (12) фиксируются полученные значения V₁(t₁), x₁(t₁), y₁(t₁), которые будут использованы при моделировании этапа 2 взлета БЛА.

Модель полета БЛА после отрыва от ВПП

На этапе 2 взлета БЛА реализуется его полет на интервале времени [t₁,t] под действием сил тяги МД и СД. Математическая модель движения БЛА на этом этапе имеет вид:

                                     (13)

Конкретизация правых частей первых двух уравнений системы (13) осуществляется с использованием выражений (1), (6)-(10). С учетом этого дифференциальные уравнения (13) интегрируются на фиксированном интервале времени [t₁,t] при следующих начальных условиях:

V₂(t₁) = V₁(t₁); q₂(t₁) = 0; x₂(t₁) = x₁(t₁); y₂(t₁) = y₁(t₁),                                   (14)

обеспечивающих связь этапов 1 и 2 взлета БЛА.

Полученные при этом значения скорости V₂(t), угла наклона траектории q₂(t) и координаты x₂(t),y₂(t) ЦМ БЛА в момент времени t окончания работы СД используются в качестве начальных условий при моделировании заключительного этапа 3 взлета БЛА.

Модель полета БЛА после сброса стартового двигателя

Данный этап взлета БЛА осуществляется на интервале времени [t, t₃] до достижения им, как и выше (см. Разд. 3.2), условий вида:

V₃(t₃) ³V_min; y₃(t₃) ³h_min.                                                                              (15)

Модель движения БЛА на этапе 3 имеет вид:

                                                         (16)

Начальные условия для этой системы уравнений записываются как:

V₃(t) = V₂(t); q₃(t) = q₂(t); x₃(t) = x₂(t); y₃(t₁) = y₂(t).                                 (17)

Момент времени t₃ завершения этого этапа взлета БЛА определяется в процессе решения задачи (16), (17) текущим значением переменной t, при котором выполняются условия (15).

Из результатов проведенного моделирования следует, что время аэродромного взлета БЛА при использовании стартового ускорителя будет равно:

t_взл = t₃.                                                                                                       (18)

В настоящее время разработка комплекса программ «Взлет» для моделирования предполагаемого взлета БЛА с различных видов взлетно-посадочных полос и различных температуры окружающего воздуха.