ПРИМЕНЕНИЕ РЕГРЕССИОННОГО АНАЛИЗА ДЛЯ ВЫЯВЛЕНИЯ ФАКТОРОВ, ВЛИЯЮЩИХ НА ВАЛОВЫЙ РЕГИОНАЛЬНЫЙ ПРОДУКТ
Журнал: Научный журнал «Студенческий форум» выпуск №15(238)
Рубрика: Физико-математические науки

Научный журнал «Студенческий форум» выпуск №15(238)
ПРИМЕНЕНИЕ РЕГРЕССИОННОГО АНАЛИЗА ДЛЯ ВЫЯВЛЕНИЯ ФАКТОРОВ, ВЛИЯЮЩИХ НА ВАЛОВЫЙ РЕГИОНАЛЬНЫЙ ПРОДУКТ
Аннотация. ВВП - это сумма стоимости всех конечных товаров и услуг, произведенных внутри страны за определенный период времени (обычно за год), за вычетом стоимости импорта. ВРП широко используется для измерения экономической активности и сравнения экономических показателей между разными регионами страны. В статье рассматривается применение регрессионного анализа для выявления влияния социально-экономических показателей на численность населения.
Ключевые слова: регрессионный анализ, ВРП.
Измерение ВРП в регионах является важным инструментом для оценки экономической активности и процветания страны. Вот несколько причин, по которым измерение ВРП важно для:
Определение экономического роста региона. Сравнение экономических показателей регионов. Оценка уровня жизни. Планирование бюджета регионов.
Целью работы является исследование показателя валовый региональный продукт и факторов, оказывающих на него влияние, при помощи методов статистического анализа. Для лучшего выявления факторов была выбрана пошаговая регрессия с исключением.
Для проведения анализа выбрано 79 регионов РФ. Выявлен ряд важных показателей, которые влияют на численность населения.
Ниже представлены данные, которые содержат сведения о регионах по следующим показателям:
y - Валовой региональный продукт, млн руб.
x1 - Площадь территории тыс.кв.м.
x2- Численность населения на начало года., тыс. человек
x3- Среднегодовая численность занятых, тыс. человек
x4 - Среднедушевые денежные доходы (в месяц), руб.
x5 - Потребительские расходы в среднем на душу населения (в месяц), руб.
x6- Среднемесячная номинальная начисленная заработная плата работников организаций, руб.
х7 - Инвестиции в основной капитал, млн руб.
х8 - Основные фонды в экономике (по полной учетной стоимости; на конец года),млн руб.
х9 – Продукция сельского хозяйства - всего, млн руб.
х10 – Ввод в действие жилых домов тыс. кв.м общей площади жилых помещений
х11 – Оборот розничной торговли, млн руб.
х12 - Сальдированный финансовый результат (прибыль минус убыток) деятельности организаций, млн руб.
В связи с небольшим количеством наблюдений – 79, для проведения анализа использовался метод моделирования измеряемых данных и исследования их свойств.
Регрессионный анализ - широко применяемый статистический метод, используемый для исследования взаимосвязи между зависимыми и объясняющими переменными. Он также является общим термином для различных методов анализа данных в качественном исследовании, используемых для моделирования и анализа множества переменных. В регрессионном анализе зависимая переменная является предиктором, а независимая переменная - результатом. Основная задача - выявить факторы, оказывающие наибольшее влияние на зависимую переменную.
Построение регрессионной модели осуществляется при помощи программы «Statistica». Необходимо построить корреляционную матрицу, описывающую зависимости между рассматриваемыми факторами, оценить эти зависимости, а также произвести регрессионный анализ вышеописанных факторов.
Проверим коллинеарность факторов, построив матрицу парных коэффициентов:
Таблица 1.
Матрица парных коэффициентов корреляции
|
|
Y1 |
X1 |
X3 |
X5 |
X6 |
X7 |
X8 |
X9 |
X11 |
X12 |
|
Y1 |
1,00 |
0,36 |
0,75 |
0,44 |
0,27 |
0,98 |
0,97 |
0,33 |
0,70 |
0,92 |
|
X1 |
0,36 |
1,00 |
0,09 |
0,33 |
0,50 |
0,37 |
0,25 |
-0,13 |
0,05 |
0,50 |
|
X3 |
0,75 |
0,09 |
1,00 |
0,37 |
-0,01 |
0,71 |
0,80 |
0,66 |
0,95 |
0,55 |
|
X5 |
0,44 |
0,33 |
0,37 |
1,00 |
0,71 |
0,44 |
0,46 |
0,17 |
0,45 |
0,32 |
|
X6 |
0,27 |
0,50 |
-0,01 |
0,71 |
1,00 |
0,29 |
0,24 |
-0,26 |
0,04 |
0,29 |
|
X7 |
0,98 |
0,37 |
0,71 |
0,44 |
0,29 |
1,00 |
0,95 |
0,30 |
0,67 |
0,91 |
|
X8 |
0,97 |
0,25 |
0,80 |
0,46 |
0,24 |
0,95 |
1,00 |
0,37 |
0,80 |
0,84 |
|
X9 |
0,33 |
-0,13 |
0,66 |
0,17 |
-0,26 |
0,30 |
0,37 |
1,00 |
0,59 |
0,18 |
|
X11 |
0,70 |
0,05 |
0,95 |
0,45 |
0,04 |
0,67 |
0,80 |
0,59 |
1,00 |
0,48 |
|
X12 |
0,92 |
0,50 |
0,55 |
0,32 |
0,29 |
0,91 |
0,84 |
0,18 |
0,48 |
1,00 |
Из матрицы видно, что коэффициент корреляции между «Валовой региональный продукт, млн руб.» (Y) и «Инвестиции в основной капитал, млн руб.» (X7) равен 0,98, «Валовой региональный продукт, млн руб.» (Y) и «Основные фонды в экономике (по полной учетной стоимости; на конец года),млн руб.» (Х8) равен 0,96 и «Валовой региональный продукт, млн руб.» (Y) и «Сальдированный финансовый результат (прибыль минус убыток) деятельности организаций, млн руб.» (Х12) равен 0,92, что больше 0,8, данный факт говорит о тесной линейной зависимости. Также в данной модели коллинеарность присутствует между (X2) «Численность населения на начало года., тыс. человек» и (X3) «Среднегодовая численность занятых, тыс. человек», (Х2) и (Х10) «Ввод в действие жилых домов тыс. кв.м общей площади жилых помещений», (Х2) «Численность населения на начало года., тыс. человек» и (Х11) «Оборот розничной торговли, млн руб.», (X3) «Среднегодовая численность занятых, тыс. человек» и (Х10) «Ввод в действие жилых домов тыс. кв.м общей площади жилых помещений», (X3) «Среднегодовая численность занятых, тыс. человек» и (Х11) «Оборот розничной торговли, млн руб.», (Х4) «Среднедушевые денежные доходы (в месяц), руб.» и (Х5) «Потребительские расходы в среднем на душу населения (в месяц), руб.), (Х4) «Среднедушевые денежные доходы (в месяц), руб.» и (Х6) «Среднемесячная номинальная начисленная заработная плата работников организаций, руб.», (Х7) «Инвестиции в основной капитал, млн руб.» и (Х8) «Основные фонды в экономике (по полной учетной стоимости; на конец года),млн руб.», (Х7) «Инвестиции в основной капитал, млн руб.» и (Х12) «Сальдированный финансовый результат (прибыль минус убыток) деятельности организаций, млн руб.», (Х8) «Основные фонды в экономике (по полной учетной стоимости; на конец года),млн руб.» и (Х12) «Сальдированный финансовый результат (прибыль минус убыток) деятельности организаций, млн руб.», (Х10) ) «Ввод в действие жилых домов тыс. кв.м общей площади жилых помещений» и (Х11) «Оборот розничной торговли, млн руб.». Коллинеарные факторы не стоит одновременно включать в модель, поэтому исключаем факторы X2, Х4 и Х10 из модели. После исключения коллинеарных факторов строим матрицу.
Таблица 2.
Матрица парных коэффициентов корреляции после исключения коллинеарных факторов
|
|
Y1 |
X1 |
X3 |
X5 |
X6 |
X7 |
X8 |
X9 |
X11 |
X12 |
|
Y1 |
1,00 |
0,36 |
0,75 |
0,44 |
0,27 |
0,98 |
0,97 |
0,33 |
0,70 |
0,92 |
|
X1 |
0,36 |
1,00 |
0,09 |
0,33 |
0,50 |
0,37 |
0,25 |
-0,13 |
0,05 |
0,50 |
|
X3 |
0,75 |
0,09 |
1,00 |
0,37 |
-0,01 |
0,71 |
0,80 |
0,66 |
0,95 |
0,55 |
|
X5 |
0,44 |
0,33 |
0,37 |
1,00 |
0,71 |
0,44 |
0,46 |
0,17 |
0,45 |
0,32 |
|
X6 |
0,27 |
0,50 |
-0,01 |
0,71 |
1,00 |
0,29 |
0,24 |
-0,26 |
0,04 |
0,29 |
|
X7 |
0,98 |
0,37 |
0,71 |
0,44 |
0,29 |
1,00 |
0,95 |
0,30 |
0,67 |
0,91 |
|
X8 |
0,97 |
0,25 |
0,80 |
0,46 |
0,24 |
0,95 |
1,00 |
0,37 |
0,80 |
0,84 |
|
X9 |
0,33 |
-0,13 |
0,66 |
0,17 |
-0,26 |
0,30 |
0,37 |
1,00 |
0,59 |
0,18 |
|
X11 |
0,70 |
0,05 |
0,95 |
0,45 |
0,04 |
0,67 |
0,80 |
0,59 |
1,00 |
0,48 |
|
X12 |
0,92 |
0,50 |
0,55 |
0,32 |
0,29 |
0,91 |
0,84 |
0,18 |
0,48 |
1,00 |
Далее строим уравнение регрессии. Для этого выбираем процедуру оценивания «Пошаговая с исключением» на каждом шаге.
Результаты множественной регрессии на шаге 4 представлены на таблицу 2. В модели остаются факторы (X3) «Среднегодовая численность занятых, тыс. человек», (Х7) «Инвестиции в основной капитал, млн руб.», (Х8) «Основные фонды в экономике (по полной учетной стоимости; на конец года),млн руб.», (Х11) «Оборот розничной торговли, млн руб.» и (Х12) «Сальдированный финансовый результат (прибыль минус убыток) деятельности организаций, млн руб.».
Построим уравнение регрессии по полученным факторам.
Таблица 3.
Регрессия
|
|
БЕТА |
Ст.Ош. БЕТА |
B |
Ст.Ош. В |
t(73) |
p-знач. |
|
Св.член |
|
|
-28805,736 |
25723,75 |
-1,11981 |
0,266465 |
|
X3 |
0,236335 |
0,044842 |
427,899 |
81,19 |
5,27036 |
0,000001 |
|
X7 |
0,326458 |
0,055528 |
1,364 |
0,23 |
5,87915 |
0,000000 |
|
X8 |
0,403261 |
0,060718 |
0,097 |
0,01 |
6,64151 |
0,000000 |
|
X11 |
-0,182998 |
0,050614 |
-0,551 |
0,15 |
-3,61552 |
0,000548 |
|
X12 |
0,247982 |
0,033243 |
0,957 |
0,13 |
7,45972 |
0,000000 |
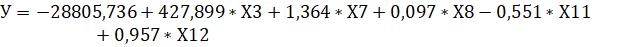
Связь высокая, так как множественный R равен 0,9941. Доля дисперсии объясненной регрессией (R2) составляет 98%. F-Статистика равна 1245,7.
В результате регрессионного анализа выяснилось:
1. Если «Среднегодовая численность занятых, тыс. человек» (Х3) увеличится на 1 тыс. чел., то «Валовой региональный продукт, млн руб.» (Y) увеличится на 427,899 млн. руб. при прочих неизменных факторах;
2. Если «Инвестиции в основной капитал, млн руб.» (X7) увеличатся на 1 млн.руб., то «Валовой региональный продукт, млн руб.» (Y) увеличится на 1,364 млн.руб. при прочих неизменных факторах.
3. Если «Основные фонды в экономике (по полной учетной стоимости; на конец года),млн руб.» (Х8) увеличатся на 1 млн.руб., то «Валовой региональный продукт, млн руб.» (Y) увеличится на 0,097 млн.руб. при прочих неизменных факторах.
4. Если «Оборот розничной торговли, млн руб.» (Х11) увеличатся на 1 млн. руб., то «Валовой региональный продукт, млн руб.» (Y) уменьшится на 0,551 млн.руб. при прочих неизменных факторах.
5. Если «Сальдированный финансовый результат (прибыль минус убыток) деятельности организаций, млн руб.» (Х12) увеличатся на 1 млн.руб., то «Валовой региональный продукт, млн руб.» (Y) увеличится на 0,957 млн.руб. при прочих неизменных факторах.

