ОПТИМАЛЬНОЕ РЕШЕНИЕ ОДНОЙ ЭКОНОМИЧЕСКОЙ ЗАДАЧИ ЕГЭ

Нами был предложен метод решения одной экономической задачи из сборника задач ЕГЭ 2023 года под редакцией И. В. Ященко [1, с. 34]. В 2021 году по архивным данным в резервный день ЕГЭ по математике профильного уровня была дана следующая задача.

Задача №17. (Резерв ЕГЭ-2021)

15 декабря 2024 года планируется взять кредит в банке на 31 месяц. Условия его возврата таковы:

‐ 1‐го числа каждого месяца долг возрастает на 2 % по сравнению с концом предыдущего месяца;

‐ с 2‐го по 14‐е число каждого месяца необходимо выплатить часть долга;

‐ 15‐го числа каждого месяца с 1‐го по 30‐й (с января 2025 года по июнь 2027 года включительно) долг должен быть на одну и ту же сумму меньше долга на 15‐е число предыдущего месяца;

‐ 15 июня 2027 года долг составит 100 тысяч рублей;

‐ 15 июля 2027 года кредит должен быть полностью погашен.

Какую сумму планируется взять в кредит, если общая сумма выплат после полного его погашения составит 555 тысяч рублей?

Для решения задачи из сборника ЕГЭ 2023 [2, с. 35] мы использовали математическую модель: «ОБЩАЯ СУММА ВЫПЛАТ = ДОЛГ (КРЕДИТ) + СУММА ПРОЦЕНТОВ», данная модель работает и для решения вышеизложенной задачи. Рассмотрим решение этой задачи.

Для удобства сумму кредита обозначим через .

Тогда долги по месяцам распределятся следующим образом:

, , …, , .

Легко заметить, что эта последовательность удовлетворяет условию задачи.

Выпишем начисленные проценты по месяцам:

, ), …, , .

Найдем сумму процентов, начисленных по месяцам:

.

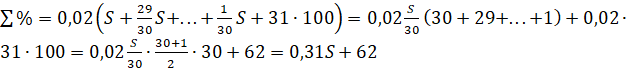Тогда на основании нашей модели получим: ,

,

, откуда  (тыс. рублей).

Ответ:  (тыс. рублей).

Эта же модель работает и для решения задач с другими неизвестными параметрами.

Задача №17.

15 декабря 2024 года планируется взять кредит в банке на сумму 400 тысяч рублей на 31 месяц. Условия его возврата таковы:

‐ 1‐го числа каждого месяца долг возрастает на % по сравнению с концом предыдущего месяца;

‐ с 2‐го по 14‐е число каждого месяца необходимо выплатить часть долга;

‐ 15‐го числа каждого месяца с 1‐го по 30‐й (с января 2025 года по июнь 2027 года включительно) долг должен быть на одну и ту же сумму меньше долга на 15‐е число предыдущего месяца;

‐ 15 июня 2027 года долг составит 100 тысяч рублей;

‐ 15 июля 2027 года кредит должен быть полностью погашен.

Найдите , если известно, что общая сумма выплат после полного его погашения составит 555 тысяч рублей?

Решение.

Для удобства кредит запишем в виде .

Тогда долги по месяцам распределятся след образом:

, , …, , .

Выпишем начисленные проценты по месяцам:

, ), …, , .

Найдем сумму процентов, начисленных по месяцам:

.

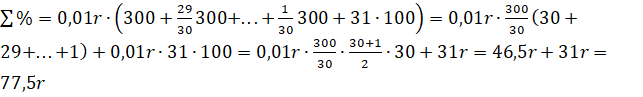Тогда на основании нашей модели: ,

,

,

.

Ответ: 2%.

Безусловно, решение экономических задач такого типа ученики, студенты и учителя могут найти и на просторах интернета, но предложенная нами модель привлекательна своей универсальностью и простотой в понимании.