Криптографиялық талдаудағы параллель есептеулер
Журнал: Научный журнал «Студенческий форум» выпуск №15(151)
Рубрика: Технические науки

Научный журнал «Студенческий форум» выпуск №15(151)
Криптографиялық талдаудағы параллель есептеулер
Аннотация. Мақалада қазіргі заманғы ақпараттық қауіпсіздіктің криптографиялық жүйелерін талдау уақытын қысқарту үшін үлестірілген мультипроцессорлық есептеулерді қолдану мәселелері қарастырылған. Блоктық шифрлау алгоритмдерін дифференциалды криптоанализ және асимметриялық криптожүйелердің дискретті логарифмдік әдістері сияқты талдау әдістері қарастырылған. Симметриялық және асимметриялық шифрлау алгоритмдерін талдаудың параллель алгоритмдерін іске асыру негізінде алынған тәжірибелік мәліметтер келтірілген.
Түйін сөздер: Криптография; криптоанализ; факторизация әдістері; өрісті елеуіш; параллельді ыдырау; Гауссты жою; құпия кілт; блоктық шифр; беріктік; үлестірілген көппроцессорлы есептеу.
Ақпаратты қорғаудың барлық дерлік бағдарламалық-аппараттық әдістері криптографиямен тығыз байланысты. Криптография көптеген ғасырлар бойы болғанына қарамастан, біз оны қазір білетін және қолданатын формада бірнеше онжылдықтарға барады. Қазіргі заманғы криптографияның дамуындағы басты (бірақ жалғыз емес) бағыт күшті шифрлау алгоритмдерін құру болып табылады деп айтуға болады. Барлық қолданыстағы шифрлар құру принципі бойынша және құпия кілтті қолдану арқылы симметриялы және асимметриялы болып бөлінеді. Жобалау кезеңінде жасалған кез-келген шифрлау алгоритмі оның әлсіз жақтарын және бұзу мүмкіндігін анықтау үшін мұқият талданады. Қолданылған шифрдың беріктігін бағалау үшін тиімді талдау алгоритмдері болуы қажет.
Бүгінгі таңда симметриялы блоктық шифрларды талдаудың әртүрлі тәсілдеріне негізделген бірнеше түрлі әдістері бар. Талдаудың ең танымал әдістеріне, мысалы, сызықтық талдау әдісі, дифференциалды талдау әдісі, мүмкін емес дифференциалдар әдісі, бумеранг шабуылы, алгебралық талдау әдісі, слайдты шабуыл әдісі жатады.
Асимметриялық криптожүйелер үшін әртүрлі әдістер де бар. Олардың ішінде ең танымал әдістер - Гельфонд әдісі, «алып өгей-сәби қадамы», кездейсоқ ағашта кездесу әдісі, негізді кеңейту әдісі, сандық өрістер әдісі, Ферма әдісі, жалғасқан фракциялар әдісі, квадратты елеу әдісі және т.б. Алайда, егер симметриялы криптожүйелерді талдауда әр түрлі әдістер линиялау, жұп мәтіндерді қарастыру, артық анықталған теңдеулер жүйесін құрастыру сияқты әр түрлі тәсілдерді қолданса, онда асимметриялық криптожүйелерді талдауда барлық әдістер азаяды екі есепті әр түрлі тәсілмен шешуге - дискретті логарифмге және үлкен сандарды көбейтуге арналған есеп.
Қуатты есептеу ресурстарының пайда болуымен қазіргі заманғы криптожүйелерді талдау міндеті таза теориялықтан практикалыққа айналды. Сонымен бірге, жоғарыда аталған көптеген әдістер параллелизацияға мүмкіндік береді, демек, олар тиісті есептеу құралдарының көмегімен бірнеше есе жылдам жұмыс істей алады. Әр түрлі криптожүйелерді талдауда өнімділігін арттыру тәсілдерінің бірі - талдау процесін жеделдету және нәтижеге тезірек жету үшін үлестірілген мультипроцессорлық есептеуді қолдану (DMP). RMB қолдану симметриялы блоктық шифрларды криптоанализдеу кезінде де, қазіргі асимметриялық криптожүйелерді талдау әдістерін қолдану кезінде де мүмкін. Таратылған есептеуді қолдану кластерлік жүйелерге арналған заманауи қолданбалы пакеттерге негізделуі мүмкін. Бұл жұмыста біз Message Passing Interface (MPI) стандартын қолдануға негізделген іске асыруды қарастырамыз.MPI оның көп платформасы, ыңғайлы интерфейсі, икемді конфигурациясы және бір компьютерден екіншісіне оңай тасымалдануы үшін таңдалған. Хабарлама жіберу моделіндегі параллель программа дегеніміз - бір уақытта өңделетін қарапайым дәйекті бағдарламалардың жиынтығы. Әдетте, осы кезекті бағдарламалардың әрқайсысы өзінің жеке процессорында орындалады және өзіндік, жергілікті жадыға қол жеткізе алады [1]. Есептеуді ұйымдастырудың айқын артықшылығы - бұл бір процессорлық жүйеде бағдарлама жазу және оны жөндеу мүмкіндігі. Есептеу жылдамдығын арттыру үшін бірдей конфигурациясы бар және жоғары жылдамдықты байланыс желісі арқылы байланысқан компьютерлерді қолдану қажет екенін ескеру қажет.
RMB көмегімен шифрлау алгоритмдерін тестілеуге арналған бағдарламаларды жасау кезінде тексерілген алгоритмде қолданылған раунд саны және шабуылды сәтті жүзеге асыру үшін қажетті мәліметтер мөлшері сияқты ерекшеліктерді ескеру қажет. Әдетте, криптаналитикалық шабуылдар екі кезеңде жүреді. Бірінші кезеңде алгоритм параметрлерін алғашқы өңдеу және барлық деректерді талдауға дайындау орындалады, оны әдетте негізгі процессор деп аталатын бір процессор орындайды. Екінші кезең алгоритмді тікелей талдаудан тұрады, ол көп жағдайда зерттелетін алгоритмді пайдаланып деректерді шифрлау үшін қолданылатын құпия кілтті табуға дейін барады. Сонымен бірге жоғарыда аталған кезеңдерді орындайтын бағдарлама бөліктерінің дұрыс және білікті өзара байланысы ұйымдастырылуы керек. Сонымен қатар, бағдарлама есептеулерде кез-келген процессор санын пайдалануға мүмкіндік беруі керек, әзірленген алгоритмді қолданғанда талдау үшін мәліметтер біркелкі бөлінуі керек.
Бұл мақалада біз RMB көмегімен түрлі криптографиялық алгоритмдерді зерттеу бойынша көпжылдық жұмыстарды қорытындылауға тырысамыз.
1. Симметриялық шифрлау алгоритмдерін талдау.
1.1. Дифференциалды талдау әдісі туралы қысқаша ақпарат. Дифференциалды криптоанализ әдісі алғаш рет 90-шы жылдардың басында ұсынылды. өткен ғасырда DES шифрлау алгоритмін талдау үшін Э.Бихам және А.Шамир [2, 3]. Жалпы, блоктық шифрлау алгоритмдерінің дифференциалды анализі келесі негізгі пункттерге дейін азаяды:
- Шифрлеу алгоритмінің максималды ықтималдылық сипаттамаларын табу. Сипаттамаларды іздеу шифрлау алгоритміне кіретін сызықтық емес криптографиялық примитивтердің дифференциалды қасиеттеріне негізделген.
- Табылған сипаттамаларды қолдана отырып, мәтіндердің дұрыс жұптарын іздеу.
- Мәтіндердің дұрыс жұптарын талдау және құпия шифрлау кілтінің мүмкін мәндері бойынша статистиканы жинақтау.
Бірінші қадамда алгоритмдердің көпшілігінің ең жақсы сипаттамаларын табу бір рет орындалады және ол теориялық тапсырма болып табылады. Сипаттамалардың мәні толығымен шифрлау алгоритмінің құрылымына және қолданылған криптографиялық примитивтерге байланысты. Алгоритмдерде тұрақты емес элементтері бар жағдай ғана басқаша. Бұл алгоритмдерге, мысалы, шифрлау алгоритмі ГОСТ 28147-89 кіреді, ол үшін ауыстырудың S-блоктарын ерікті түрде таңдауға болады. Мұндай алгоритмдер үшін таңдалған S-өрістерінің дифференциалды қасиеттеріне сүйене отырып, сипаттамаларды іздеуді әр басынан бастау керек. Талдау процесін автоматтандыру үшін ағаш іздеу алгоритмі негізінде ең жақсы сипаттамаларды табудың алгоритмін жасауға болады. Мұндай алгоритмдер үшін параллельді модельдерді сипаттамаларды іздеуді жылдамдату үшін пайдалануға болады.
Талдаудың екінші кезеңі кез-келген шифрлау алгоритмі үшін есептік сенімді тапсырма болып табылады, оның тіркелген немесе бекітілмеген элементтері маңызды емес. Талдау мәтіндердің дұрыс жұбы екенін, яғни құпия шифрлау кілтін табу үшін әрі қарай талдау үшін қолдануға болатын мәтіндер жұбын анықтау үшін көптеген жұп мәтіндерді тексеруден тұрады. Бұл қадам талдау уақытын қысқарту үшін параллельді есептеулер түрінде оңай ұсынылуы мүмкін және болуы керек.
Соңғы қадамды орындау оңай және екінші кезеңге қарағанда есептеуді азырақ қажет етеді. Оны дәйекті алгоритм ретінде жеке-жеке жүзеге асыруға болады немесе дұрыс мәтін жұптарын табудың параллель алгоритмдеріне қосуға болады. Екінші жағдайда, мәтіндердің дұрыс жұбы табылған кезде оны құпия кілттің мүмкін болатын мәні туралы статистиканы жинақтап бірден талдауға болады.
1.2. DES алгоритмінің дифференциалды криптоанализі. Э.Бихам және А.Шамир ұсынған әдістер мен тәсілдердің негізінде [2, 3] құпия шифрлау кілтін табу үшін DES шифрлау алгоритмін талдаудың егжей-тегжейлі бағдарламалық бағдарланған дәйекті және параллель алгоритмдер тобы жасалды. Осы алгоритмдер туралы толығырақ ақпаратты [6] табуға болады.
DES дифференциалды криптоанализін жүргізудің жасалған алгоритмдері негізінде RMB көмегімен шифрлаудың кез келген санын талдауға мүмкіндік беретін бағдарлама іске асырылды. Бұл бағдарлама Microsoft Visual C ++ 6.0 бағдарламалау ортасында мультипроцессорлық есептеу үшін қолданылатын MPICH 1.2.5 пакетінің талаптарына байланысты жасалған. Осы бағдарламаның көмегімен DES шифрының 6 раунын ең ықтимал дифференциалдарды қолдану арқылы талдау алгоритмі тексерілді. Тәжірибелік мәліметтер көрсеткендей, DES алгоритмін 6 раундты талдау әрқашан дұрыс нәтиже береді. 2 процессорлы жүйеде (жиілігі 2,67 ГГц жиілікте) талдау уақыты орташа есеппен 7,5 минутты, 16 процессорлы жүйеде 56 секундты құрайды. Құпия кілттің әртүрлі мәндеріне тексеру жүргізілді. N-процессор жүйесіндегі құпия кілттің әр түрлі мәндерін талдау уақыты орташа есеппен 3-5 секундқа ерекшеленді, бұл қолданылатын амалдық жүйеге және мәліметтерді беру ортасына байланысты және есептеудегі табиғи қателік уақыт.
Жүргізілген екінші сынақ - 2,67, 2,67 ГГц процессорлары бар 2, 3, 4 және 5 процессорлық жүйелердегі 8, 10, 12, 14 және 16 айналымнан тұратын DES алгоритмін толық талдау. Тәжірибе нәтижелері кестеде көрсетілген. 1. Әр эксперимент (әсіресе аз мөлшерде қолданылатын процессорлармен) өте ұзақ процесс болғандықтан, эксперименттер K_L = 2882400171, K_R = 3455036365 құпия кілтінің бір мәні үшін жүргізілді. Үстелден. 1, есептеулерге қатысатын процессорлар санының артуымен, талдау уақытының үдеуінің сызықтық өсуі байқалады. Суретте көрсетілген графиктен де осыны байқауға болады. 1. Бұл график кестеге сәйкес салынған. 1. Абциссада процессорлардың саны, ал ординатада анализге кеткен уақыт көрсетіледі.
1,41 ГГц жиіліктегі 16 процессорлық кластер үшін DES алгоритмінің 16 айналымнан тұратын уақыты 24 сағат 13 минутты құрады.
Кесте 1.
DES шифрлау алгоритмін талдау нәтижелері
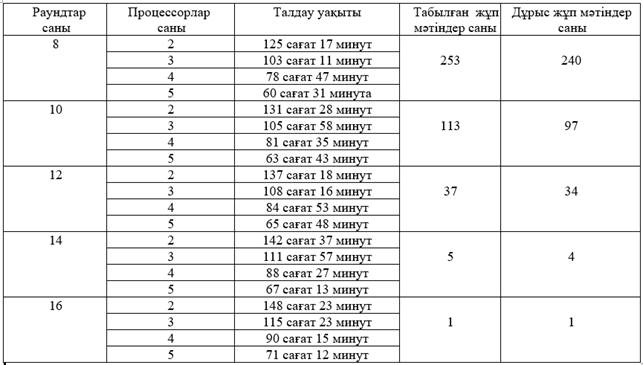
1.3. ГОСТ 28147-89 алгоритмін дифференциалды талдау. ГОСТ алгоритмінің айрықша ерекшелігі - оның құрамына тұрақты емес ауыстыру блоктарының болуы, олар әр уақытта әр түрлі болуы мүмкін. Осыған байланысты, ГОСТ алгоритмі үшін максималды ықтималдықтармен сипаттамаларды іздеу үшін дифференциалды криптоанализдің бірінші кезеңі басталуы керек. Біздің жұмысымыздың нәтижесінде максималды ықтималдықтармен сипаттамаларды табудың параллель алгоритмін жасадық. Бұл алгоритм туралы толық мәліметтерді [6, 7] табуға болады.
Жұмыс нәтижесінде дамыған параллель алгоритм негізінде екі бағдарлама іске асырылды: біреуі статикалық деректерді тарату, екіншісі динамикалық қолдану. Екі бағдарлама да 16 процессорлық кластердің көмегімен сыналды (1,41 ГГц процессор жиілігі). Сынақ эксперименттері кезінде есептеу жылдамдығы әртүрлі бастапқы шарттар бойынша өлшенді: есептеулерге қатысқан процессорлар саны, шифрлау дөңгелектерінің саны және шекті ықтималдылықтың бастапқы мәні. Нақты уақыт режимінде ГОСТ 28147-89 8-раундтық шифрлау алгоритмінің нәтижелерін алуға болатын. Бұл жағдайда әрбір дөңгелек алгоритм үшін (мұндағы n ≤ 8) шекті ықтималдықтың екі түрлі бастапқы мәндері үшін уақыт өлшенді: 0-ге тең және 0-ден өзгеше.

Сурет 1. DES алгоритмінің n-айналымдарын талдау уақыты
Деректердің статикалық таралуы бар бағдарламаның эксперименттік нәтижелері суретте көрсетілген графиктерде жинақталған. 2. Процесс # 0 жалпы бағдарламаның жалпы жұмыс уақытын көрсетеді. Егер оны есептеу уақытының өсуін қалған процестермен салыстыратын болсақ, онда шифрлаудың 5 айналымына дейін, мүмкін шығыс мәліметтерінің көлемі барлық кейінгісі сияқты күрт өспейтіні белгілі болады, бұл графикте көрсетілген . Графиктер 7-ші және 8-ші раундтағы шифрлау алгоритмінің нүктелерін көрсетпейді, өйткені оларды есептеу уақыты 2, 3, 4, 5 және 6 айналымдарға қарағанда әлдеқайда көп. Сондықтан, егер алынған мәліметтерді бірге ұсынатын болсақ, дөңгелектер саны 7-ден кем болатын алгоритмдер үшін шифрлау есептеу жылдамдығының өзгеру динамикасын көрмейміз. 2-де әр түрлі процестерге арналған 5 айналымға дейін (атап айтқанда, 4, 6 және басқалары үшін) есептеу уақыты әрдайым шифрлау дөңгелектері санының артуымен өсе бермейтінін, ал кейбір жағдайларда тіпті айтарлықтай төмендейтіндігін көрсетеді. Бұл бірнеше факторларға байланысты, атап айтқанда: шифрлау дөңгелектері санының артуымен есептеулердің салыстырмалы түрде аз өсуімен, тарату ортасындағы қателіктермен, шекті ықтималдықтардың процессорлармен алмасу ерекшеліктерімен. Тәжірибелер көрсеткендей, ең қарқынды процессорлық алмасу есептеудің алғашқы 15 секундында жүреді (бұл 5 раундтық алгоритмге дейінгі есептеу уақытын ғана қамтиды). Кейіннен айырбас процестердің біреуі шекті мәннен асып кету ықтималдығын тапқан кезде тек анда-санда жүреді. 7 айналымнан асатын шифрлау алгоритмін талдау кезінде мұндай секірулер байқалмайды.
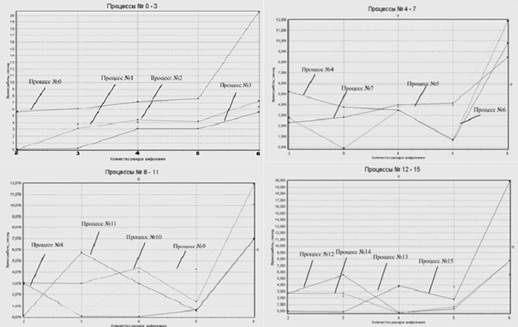
Сурет 2. Деректерді статикалық тарату бағдарламасы бойынша эксперименттердің нәтижелері
Бағдарламаның нәтижесі максималды ықтималдыққа ие бір немесе бірнеше жұп кіріс және шығыс ықтималдығы болып табылады. Бекітілген алмастыру блоктары бар 7-дөңгелек алгоритм үшін p = 1.591252e-008 ықтималдығымен осындай бір ғана жұп табылды.
Мәліметтердің динамикалық таралуы бар бағдарлама үшін n-7 шифрлау алгоритмінің жұмыс жылдамдығы статикалық үлестірімге қарағанда сәл жақсы болып шықты (2-кестеде 6-дөңгелек алгоритмге арналған эксперименттік мәліметтер келтірілген). Сонымен қатар, барлық процессорлар бірдей жүктемені алды, және сәйкесінше, шамамен бірдей жұмыс уақыты, статикалық алгоритмнен айырмашылығы, мұнда кейбір процестер басқаларына қарағанда жылдамырақ қарастырылды. Алайда, жеті айналыммен жұмыс уақыты статикалық үлестіріліммен бағдарламаның жұмыс уақытынан едәуір асып түседі. Бұл барлық процессорлардың жүктемесі бірдей болғанына қарамастан. Бір қарағанда, мұндай оқиғаның мүмкін еместігі қарапайым түсіндіріледі: статикалық үлестіріммен талдау процестері әртүрлі диапазондардан мәндер алады. Осы мәндердің бірі мүмкін болатын максимумға өте жақын ықтималдығы бар кіріс-шығыс айырмашылық жұбын бірден дерлік анықтауға мүмкіндік береді. Процессораралық байланыстың арқасында бұл ықтималдық мәні барлық процестер үшін шекті мәнге айналады. Демек, одан әрі талдау айқын нашар жұптардан бас тарту арқылы жүзеге асырылады, яғни ықтималдығы ағымдағы шекті мәннен төмен. Мәліметтерді динамикалық тарату кезінде ықтималдықтың мұндай жақсы мәні бірден анықталмайды, сондықтан процестер бүкіл ағаштың бойында қайталануы керек, бұл талдау процесін едәуір баяулатады.
Осыған сүйене отырып, жасалынған алгоритмдерді қолданудың тиімділігі тек қолданылатын процессорлар санына және шифрлау айналымдарының санына ғана емес, сонымен қатар талдау мәліметтерін тарату әдісіне байланысты деген қорытынды жасауға болады. Мүмкіндікке неғұрлым жақын болатын ықтималдығы неғұрлым тез табылса, соғұрлым тезірек талдау жасалады. Әр түрлі алмастыру блоктарының дифференциалды криптоанализде әр түрлі мағынаға ие болатындығын есте ұстаған жөн, сондықтан алмастыру блоктарының әр түрлі жиынтығы үшін әр түрлі кіріс ықтималдығы шифрлау айналымдарынан өту кезінде ең жақсы ықтималдық береді.
Кесте 2.
Мәліметтерді динамикалық таратумен алгоритмге арналған тәжірибелік деректер
|
Процесстер нөмірі |
1 |
2 |
3 |
4 |
|
Талданған мәндер саны |
6 |
5 |
7 |
4 |
|
Жұмыс уақыты, секунд |
10,63264 |
10,78271 |
11,09175 |
11,96433 |
|
Процесстер нөмірі |
5 |
6 |
7 |
8 |
|
Талданған мәндер саны |
5 |
13 |
6 |
10 |
|
Жұмыс уақыты, секунд |
10,27041 |
11,53331 |
11,40407 |
10,84244 |
|
Процесстер нөмірі |
9 |
10 |
11 |
12 |
|
Талданған мәндер саны |
7 |
4 |
11 |
6 |
|
Жұмыс уақыты, секунд |
10,75531 |
10,13938 |
10,22375 |
10,93916 |
|
Процесстер нөмірі |
13 |
14 |
15 |
16 |
|
Талданған мәндер саны |
6 |
10 |
8 |
11 |
|
Жұмыс уақыты, секунд |
10,65408 |
14,16819 |
10,77713 |
13,83076 |
Кесте 3.
Бағдарламаның басқа процессорлардағы жұмысының уақыт көрсеткіштері
|
Процесстер саны |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
Статикалық таралуы |
54,2 |
57,1 |
30,8 |
36,6 |
24,4 |
24,6 |
24,7 |
20,8 |
|
Динамикалық таралуы |
63,6 |
40,7 |
27,2 |
22,9 |
21,2 |
20,2 |
19,9 |
17,6 |
|
Процесстер саны |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
|
|
Статикалық таралуы |
22,06 |
18,5 |
15,5 |
18,4 |
19,8 |
18,8 |
18,8 |
|
|
Динамикалық таралуы |
15,5 |
16,5 |
18,1 |
15,6 |
17,3 |
13,4 |
14,3 |
|
Кесте 3 процессорлардың басқа санын қолдана отырып 0 ықтималдылық шегі бар 6-дөңгелек шифрлау алгоритмі үшін алынған деректерді көрсетеді. Түсінікті болу үшін, осы тәжірибелердің мәліметтері 3-суреттегі график түрінде берілген. 3-суретте әрдайым көп процессорлардың саны есептеу уақытының азаюына әкелмейтіні көрсетілген. Алайда, статикалық деректерді тарату көмегімен талдау үшін 16 процессорды қолданған кезде, есептеу процессі екі процессорлық жүйеде жасалған есептеулермен салыстырғанда 2,88 есе, динамикалық көмегімен - 4,4 есе қысқарады. Мәліметтерді динамикалық таратумен есептеулер үшін 3-суреттегі графика үдеудің сызықтық өсуі бар екенін көрсетеді. 8 немесе одан аз процессорларды қолдана отырып есептеу үшін тиімділік мәні 1,2-ден 0,8-ге дейін болады.
2. Асимметриялық криптожүйелерді талдау.
2.1. Дискретті логарифм есебін базисті кеңейту әдісімен шешу. Fp* тобындағы дискретті логарифмді есептеудің негізгі ыдырау әдісі осы топтың бүтін сандар сақинасының Z* жартылай тобына енуіне негізделген. Осы жартылай топтардың гомоморфизмінің анықтамасы бойынша Z сақинасындағы AB = C теңдігі AB ≡ C (mod p) білдіреді, Ax = B теңдігі мен Ay ≡ B (mod p) сәйкестігінен x ≡ y шығады. (mod r), мұндағы r - А элементі құрған топтың негізгі тәртібі [8, 9].
Дискретті логарифм есебін шешуге арналған ыдырау негізінің әдісінде үш негізгі кезеңді ажыратуға болады: ыдырау негізін құру, Гаусс әдісіне негізделген нөлдік емес көрсеткіштерді жою және алынған салыстыруды шешу. 1 және 2 кезеңдер есептеу жағынан күрделі, сондықтан олардың орындалуын тездету үшін D-тегіс дәрежелерді табудың параллель алгоритмі (елеу) және ыдырау негізінің элементтеріндегі нөлдік емес көрсеткіштерді жою үшін параллель Гаусс алгоритмі жасалды. 4-суретте алгоритмнің бірінші және екінші кезеңдерін параллельдеу тиімділігін көрсететін тәжірибелер нәтижелерін ұсынады.
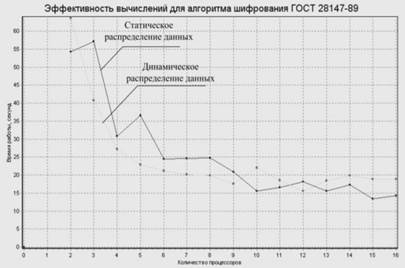
Сурет 3. Есептеу уақытының қолданылатын процессорлар санына тәуелділігі
Жасалған алгоритмдер негізінде жүзеге асырылған бағдарламалық жасақтаманы қолдану арқылы тәжірибелер SFedU (20 Intel Xeon 2,33 ГГц есептеуіш ядролары, 10 ГБ жедел жады, Gigabit Ethernet тарату ортасы) ақпараттық технологиялар қауіпсіздігі департаментінің кластерінде жүргізілді. ).
Осы графиктерді құру үшін логарифм 70 екілік цифрдан тұратын жай сан құрған топтан табылды. Негіз өлшемі 800 болды. Графиктер есептеулердің бірінші кезеңі параллелизацияға өте жақсы әсер ететіндігін көрсетеді, екінші кезеңде өнімділіктің жоғарылауы соншалықты үлкен емес. Шындығында, процестердің саны 10-нан асып кеткендіктен, өнімділіктің төмендеуі байқалады. Бұл матрица бөлімдерін параллель өңдеу есебінен өнімділіктен гөрі анықтамалық жолды процестерге ауыстыру үстеме шығыстарының басым болуына байланысты. Негіздің өлшемін кішірейту арқылы елеудің күрделілігін арттыру есебінен матрицаның өлшемін және екінші кезеңді аяқтау уақытын қысқартуға болады. Сондай-ақ, нәтиже деректерді берудің неғұрлым тиімді ортасын қолдану арқылы берілуі керек, мысалы, InfiniBand.
2.2. Дискретті логарифм есебін өрісті елеу әдісі арқылы шешу. Дискретті логарифмді есептеудің жалпы елеуіштік өріс әдісін Гордон ұсынған және Вебер жасаған [8, 9]. Әдіс алгебралық бүтін сандар сақиналарында ыдыраудың негізгі идеалдарға бірегейлігін қолданады. Қысқаша сандық өрістер әдісі арқылы дискретті логарифмді іздеуді келесі кезеңдерге дейін қысқартуға болады: ыдырау негізін құру, ыдырау негізін елеу, экспоненттер матрицасын Гаусс әдісі негізінде түрлендіру және алынған салыстыруды шешу. 2 және 3 кезеңдері есептеу жағынан күрделі, сондықтан олардың орындалуын тездету үшін D-тегіс сандарды табудың параллель алгоритмі (елеу) және параллель Гаусс алгоритмі жасалды. Осы алгоритмдер туралы толығырақ ақпаратты [10–11] табуға болады.
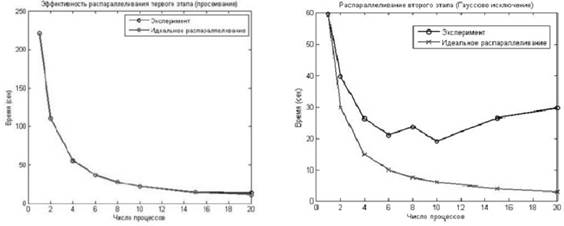
Сурет 4. Бірінші және екінші кезеңдердің параллелизациясы
Зерттеу барысында әзірленген алгоритмдер C++ тілінде OpenMPI (процессаралық байланысты қамтамасыз ету үшін), NTL және GMP (ерікті ұзындықтағы бүтін сандармен жұмыс жасау) тегін кітапханаларын қолдана отырып жүзеге асырылды. 5-суретте көрсетілген графиктер есептеу уақытының мультипроцессорлы компьютерлік жүйеде процессорлар санына тәуелділігін көрсетеді. Тәжірибе 20 Intel Xeon 2.6GHz процессор ядроларынан, 10 ГБ жедел жадыдан, Gigabit Ethernet тасымалдағышынан тұратын кластерде жүргізілді.
Ыдыраудың базалық әдісін қолдана отырып, салыстырмалы тестілеу көрсеткендей, салыстырмалы түрде аз модуль өлшемдері үшін (70-75 бит) ыдырау базалық әдісі тезірек електенеді. Өрісті елеуіштің іске асырылу уақыты негіздің мөлшеріне байланысты, бірақ оның минималды өлшемімен ол базалық кеңейту әдісін енгізу уақытынан асып түседі. Матрицалық түрлендіруге кететін уақыт екі іске асыру үшін де бірдей болады. Бұл теориялық нәтижелерге сәйкес келеді, оған сәйкес сандық өрісті елеу әдісі модульдің жеткілікті үлкен өлшемдері үшін базаны кеңейту әдісіне қарағанда жылдамырақ жұмыс істей бастайды.
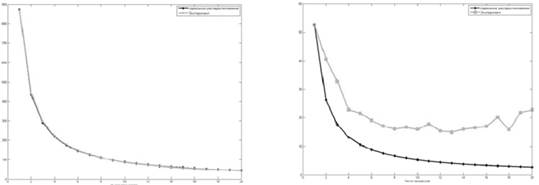
Сурет 5. Матрицалық ыдырау және түрлендірудің бірінші (сол жақ) және екінші (оң) кезеңдерін параллельдеу кезінде өнімділіктің өсуі

