Группы подстановок

Теория групп начала оформляться в качестве самостоятельного раздела математики в конце восемнадцатого века. Многие работы по теории групп посвящены исследованию класса групп, называемых группами подстановок (или группами перестановок). Группы подстановок особенно интересны тем, что с их помощью можно получить конкретные представления всех конечных групп.

Множество взаимно однозначных отображений множества из  элементов на себя составляет группу отображений. Отображение — это записанные в виде двух строк, заключенных в скобки, где элементы из области определения стоят в верхней строке, а элементы из области значений — в нижней. Такие отображения называют подстановками, а группы, элементами которых являются подстановки - группами подстановок [3].

Решение задач по теме «Группы подстановок»

1) Составить таблицу умножения в группе ; Каков порядок группы  

2) Найдите порядок каждого элемента этой группы?

3) Какие подгруппы есть в данной группе

4) Разложите эту группу по подгруппе четных подстановок.

Решения:

1) Пусть – группа всех подстановок третьей степени, т.е.

,

где

,    ,   ,

,    ,   .

Вычисляя попарные произведения этих элементов, получаем для данной группы следующую таблицу:

Таблица 1.

Попарные произведения

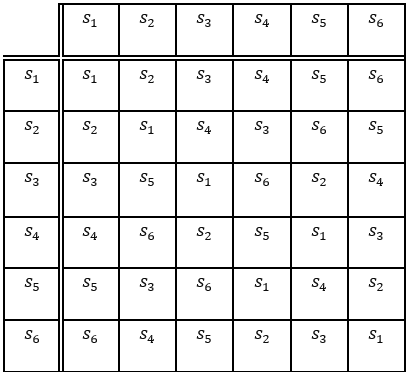
Так как в группе 6 элементов, то порядок  равен 6.

2)  – порядок элемента , если  и  – наименьшее число, для которого это выполняется [1].

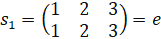
Следовательно , значит, порядок ,

, значит, порядок ,

, значит порядок ,

, значит, порядок ,

, значит, порядок ,

, значит, порядок .

3)Множество  является подгруппой группы .

4) Составим правый и левый смежные классы элемента  по подгруппе :

,

.

Таким образом левый и правый классы элемента  не совпадают. Составляя теперь правые смежные классы всех элементов группы  получим:

,  , 

, , .

Отсюда очевидно, что различных правых смежных классов оказалось только три:

, , 

поскольку классы некоторых различных элементов, например  и , совпадают (эти элементы входят в один и тот же класс).

Группа имеет следующую нормальную подгруппу : . Это подгруппа четных подстановок [2].

Вычисления, аналогичные вычислениям примера 1, показывают, что найдутся только два различных правых класса:

 и .

Правый из них является правым смежным классом для каждого из элементов подгруппы , второй – для всякого другого элемента группы .