ОПРЕДЕЛЕНИЕ ЛИЧНОЙ ПОГРЕШНОСТИ ИЗМЕРЕНИЙ
Журнал: Научный журнал «Студенческий форум» выпуск №2(181)
Рубрика: Технические науки

Научный журнал «Студенческий форум» выпуск №2(181)
ОПРЕДЕЛЕНИЕ ЛИЧНОЙ ПОГРЕШНОСТИ ИЗМЕРЕНИЙ
В статье будет рассмотрен пример определения личной погрешности измерении проводимых штангенциркулем и микрометром. Статья поможет научиться правильно выполнять измерения предложенными средствами и оценивать личную погрешность.
Основные характеристики случайной величины:
1) Среднее арифметическое
![]()
Где i - нормативный номер измерения; n - число измерений; xi- результат отдельного измерения.
2) Отклонение от среднего (погрешность измерения).
![]() =
= ![]() -
-![]()
При правильном расчете ![]()
Δ=xизм-Q (Qд)
3) Среднее квадратичное отклонение
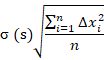
В некоторых вычислениях используют несмещенную оценку среднего квадратичного отклонения.
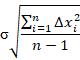
4) Дисперсия
![]()
![]()
5) Доверительная погрешность
Δx=t*σ
t=φ(q,f)
g=100-P, %; g=1-P
Где - P=95% (0,95) – нормальный; P=99% (0,99) – повышенный; P=90% (0,90) – пониженный.
f=n-1
Где - t-коэффициент Стьюдента; q-уровень значимости; f-число степеней свободы; P-доверительная вероятность (уровень надежности).
6) Минимальное число измерений
![]() 2
2
![]()
Для нахождения их, поставим для себя следующие цели:
1) Изучить устройство предложенных средств измерений.
2) Выполнить измерение толщины детали 10 раз в одной точке.
3) Рассчитать основные характеристики случайных величин (используя обычную оценку среднего квадратичного отклонения и дисперсия для двух уровней значимости q=5% и 1%, t=2,26 (q=5%, f=9), t=3,25 (q=1%, f=9)).
Рассмотрим устройство штангенциркуля, оно представлено на рисунке 1
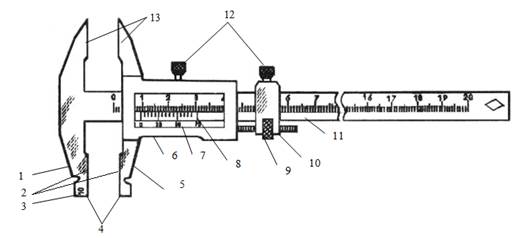
Рисунок 1. Устройство штангенциркуля: 1 – неподвижная губка, 2 - мерительные поверхности для измерения наружных размеров, 3 - маркировка ширины губок для измерения внутренних размеров, 4 - мерительные поверхности для измерения внутренних размеров, 5 – подвижная губка, 6 – рамка, 7 – нониус, 8 – основная шкала, 9 – гайка и винт для точной установки губок, 10 – движок, 11 – штанга, 12 – зажимные финты, 13- острозаточенные губки для разметки.
Для определения личной погрешности мной было взята одна деталь и произведено 10 измерений в одном и том же месте. Измерения происходили при помощи штангенциркули и микрометра. Результаты занесены в таблицу 1 и 2 соответственно.
Таблица 1
Результаты измерений штангенциркулем
|
i |
xi, мм |
Δxi, мм |
|
|
1 |
23.55 |
0.01 |
0 |
|
2 |
24.1 |
0.56 |
0.134 |
|
3 |
23.45 |
-0.09 |
0.0081 |
|
4 |
23.4 |
-0.14 |
0.0196 |
|
5 |
23.45 |
-0.09 |
0.0081 |
|
6 |
23.4 |
-0.14 |
0.0196 |
|
7 |
23.55 |
0.01 |
0 |
|
8 |
23.55 |
0.01 |
0 |
|
9 |
23.45 |
-0.09 |
0.0081 |
|
10 |
23.5 |
-0.04 |
0.0016 |
|
|
Σ=235.4 |
Σ→0 Σ=0 |
Σ=0,379 |
![]() =23,54
=23,54
σ=0,195
σ2=0.0379
Δx1=2,26*0,195=0,441
Δx2=3,25*0,195=0,634
nmin1=0,441/0,1=4.412=19.448
nmin2=0,634/0,1=6.342=40.196
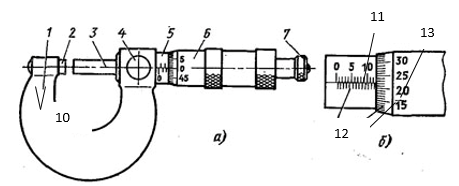
Рисунок 2. Устройство микрометра: 1 - скоба, 2 – пятка, 3 – шпиндель, 4 – стопор, 5 – стебель, 6 – барабан, 7 – трещетка, 8 – миллиметровые деления основной шкалы, 9 – круговой нониус (лимб), 10 – мерительные поверхности, 11 – крепежный винт, 12 – отсчетная линия, 13 – пулимиллиметровые деления основной шкалы.
Таблица 2
Результаты измерений микрометром
|
i |
xi, мм |
Δxi, мм |
|
|
1 |
23.27 |
-0.02 |
0.0004 |
|
2 |
23.29 |
0 |
0 |
|
3 |
23.26 |
-0.03 |
0.0009 |
|
4 |
23.29 |
0 |
0 |
|
5 |
23.26 |
-0.03 |
0.0009 |
|
6 |
23.32 |
0.03 |
0.0009 |
|
7 |
23.28 |
-0.01 |
0.0001 |
|
8 |
23.29 |
0 |
0 |
|
9 |
23.29 |
0 |
0 |
|
1 |
23.35 |
0.06 |
0.0036 |
|
|
Σ=232.9 |
Σ→0 Σ=0 |
Σ=0,0068 |
![]() =23.29 ; σ=0,026; σ2=0,00068;
=23.29 ; σ=0,026; σ2=0,00068;
Δx1=2,26*0,026=0,0587; Δx2=3,25*0,026=0,0845
nmin1=(0,0587/0,05)2=1.378 ; nmin2=(0,0845/0,05)2=2.856
Из выше изложенного можно сделать следующие выводы изучили устройство штангенциркуля и микрометра, измерила толщины деталей 10 раз в одном месте, и рассчитали основные характеристики. По результатам расчетов видно, что измерения сделанные микрометром более точны, в отличие от штангенциркуля.

