ВЗАИМОСВЯЗЬ МАКСИМАЛЬНЫХ ПРОГИБОВ И СОБСТВЕННЫХ ЧАСТОТ КОЛЕБАНИЙ ТРЕУГОЛЬНЫХ СОСТАВНЫХ МНОГОСЛОЙНЫХ ПЛАСТИН С КОМБИНИРОВАННЫМИ УСЛОВИЯМИ ОПИРАНИЯ ПО КОНТУРУ

Были рассмотрены составные пластины треугольного с прямым углом очертания в плане. Опоры по контуру плиты располагались в узлах конечных элементов конструкции, при этом граничные условия слоёв были однородными. В работе рассмотрены комбинированные условия опирания по контуру (жжж, жжш, жшш, шшш).

Численные исследования составных двухслойных пластин на податливых связях проводились методом конечных элементов. В ходе численных исследований определение прогибов и частот колебаний проводилось в программном комплексе «ЛИРА САПР». В качестве модели исследования была выбрана треугольная двухслойная составная пластина. Каждый слой был разбит сеткой 40×40 на конечные элементы (КЭ); таким образом, размер каждого конечного элемента составил 100×100 мм.

Толщина пластин задавалась различной: толщина нижней пластины принята постоянной 10 мм, толщина верхней принималась равной 4…10 мм с шагом 1 мм, 12 и 15 мм. Пластины связаны между собой поперечными  связями (препятствующими сближению и отдалению слоёв) и связями сдвига.

Рисунок 1. Общий вид расчетной модели в ЛИРА САПР

Таблица 2.1.

Численные исследование составных двухслойных квадратных пластин с комбинированными граничными условиями

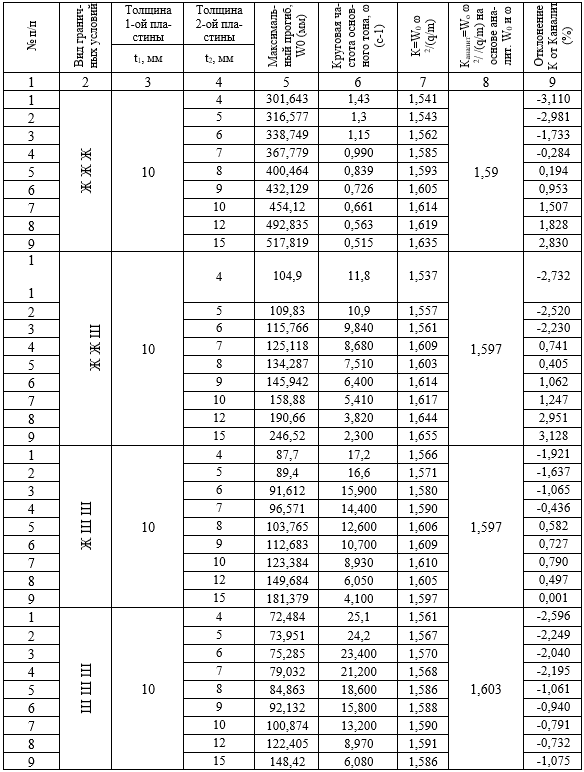
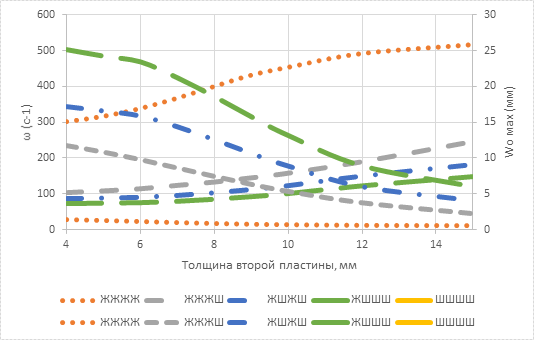
Рисунок 2. Взаимосвязь максимальных прогибов и частот собственных колебаний от отношения толщин двухслойной пластины

Анализ полученных результатов показывает, что независимо от отношения толщин слоев фундаментальная зависимость выполняется с точностью от +3,128 до -3,110% для двухслойной пластины с комбинированными граничными условиями.