ПРИМЕНЕНИЕ И АНАЛИЗ АЛГОРИТМОВ БЕЗ ПОТЕРЬ ДЛЯ СЖАТИЯ ИЗОБРАЖЕНИЙ
Секция: Технические науки

LXVII Студенческая международная научно-практическая конференция «Технические и математические науки. Студенческий научный форум»
ПРИМЕНЕНИЕ И АНАЛИЗ АЛГОРИТМОВ БЕЗ ПОТЕРЬ ДЛЯ СЖАТИЯ ИЗОБРАЖЕНИЙ
В современном мире цифровых технологий, где объемы данных растут с каждым днем, вопрос эффективного хранения и передачи информации становится все более актуальным. Особенно это касается изображений, которые занимают значительную часть интернет-трафика. Алгоритмы сжатия изображений без потерь играют ключевую роль в решении этой проблемы, позволяя уменьшить размер файлов, сохраняя при этом их первоначальное качество.
Уменьшенный файл, созданный в процессе сжатия, называется сжатым файлом и используется для восстановления изображения, что приводит к получению разжатого изображения. Отношение оригинального (несжатого файла) к сжатому файлу называется коэффициентом сжатия.
Формула для расчета коэффициента сжатия (CR) выглядит следующим образом:
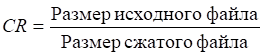 (1)
(1)
Сжатие изображений без потерь имеет широкое применение, например, в архивировании медицинских или деловых документов, цифровой радиографии, где любая потеря информации в оригинальном изображении может привести к неправильному диагнозу. Другие применения сжатия без потерь включают сжатие изображений для систем видеонаблюдения, хранение и передачу тепловых изображений, полученных наноспутниками, а также применение в дистанционном зондировании, таком как мониторинг лесных пожаров и определение влажности почвы [1].
Основные методы сжатия изображений без потерь включают следующие техники:
- Run-Length Encoding (RLE) – это простой метод сжатия данных, в котором мы разбиваем исходный файл на сегменты из одинаковых символов, каждый сегмент заменяется парой вида (символ, количество повторений) [4]. Широко применяется для сжатия изображений, текстовых данных и других последовательностей символов.
Принцип работы RLE заключается в следующем:
- идентификация серий: алгоритм проходит по последовательности символов и идентифицирует повторяющиеся серии символов. Серия — это последовательность одинаковых символов, идущих один за другим;
- кодирование серий: повторяющиеся серии заменяются кодами, состоящими из двух частей: символа и количества повторений. Например, серия из 5 символов "A" будет заменена кодом "A5". Если символ не повторяется, он остается без изменений. Таким образом, последовательность "AAABBBCCC" может быть закодирована как "A3B3C3";
- декодирование данных: при декодировании данные восстанавливаются обратно в исходную последовательность символов. Алгоритм проходит по закодированной последовательности, определяет коды серий и восстанавливает повторяющиеся символы в соответствии с указанным количеством повторений.
Преимущества RLE заключаются в его простоте и эффективности для изображений с большими областями одного цвета или повторяющихся паттернов. Он не требует сложных вычислений или большого объема памяти для кодирования и декодирования. Однако, RLE неэффективен для сложных изображений с высокой степенью детализации или случайных паттернов, где повторения редки или отсутствуют.
- Huffman Coding: Алгоритм Хаффмана – это метод сжатия данных, который использует принципы кодирования переменной длины для представления символов. Это кодирование известно как алгоритм энтропийного кодирования [2]. В контексте сжатия изображений, алгоритм Хаффмана может быть использован для уменьшения размера файла изображения без потери качества, то есть это сжатие без потерь. Алгоритм Хаффмана для сжатия изображений работает по следующему сценарию:
- анализ частоты: алгоритм начинается с анализа частоты встречаемости каждого символа (в случае изображений, это могут быть значения пикселей) в исходных данных;
- построение дерева Хаффмана: на основе частот, строится дерево Хаффмана. Листья дерева представляют символы исходных данных, а вес каждого листа соответствует частоте символа. Затем выбираются два узла с наименьшими весами и создается новый узел, вес которого равен сумме весов этих двух узлов. Этот процесс повторяется, пока не будет построено полное дерево.
На рисунке 1 представлен псевдокод алгоритма Хаффмана для построения дерева Хаффмана на основе заданного алфавита и их частоты появления.
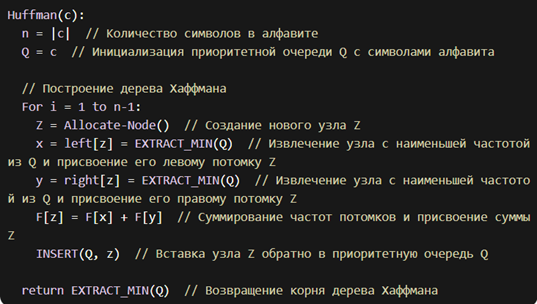
Рисунок 1. Псевдокод алгоритма Хаффмана для построения дерева Хаффмана
- кодирование: каждому символу присваивается уникальный код Хаффмана, который соответствует пути от корня дерева до листа, представляющего этот символ. Символы, которые встречаются чаще, получают более короткие коды, а редкие символы – более длинные коды;
- сжатие: используя полученные коды Хаффмана, исходные данные перекодируются в последовательность битов, что приводит к уменьшению общего размера данных;
- декодирование: для восстановления исходных данных из сжатого формата, используется дерево Хаффмана. Последовательность битов сжатого файла интерпретируется с помощью дерева, чтобы определить соответствующие символы.
Этот алгоритм широко используется во многих областях, включая сжатие JPEG-изображений и других графических объектов. Он позволяет значительно уменьшить размер файлов, сохраняя при этом их первоначальное качество. Это делает его очень полезным для хранения и передачи данных.
- Алгоритм Lempel-Ziv-Welch (LZW) – это универсальный алгоритм сжатия данных без потерь, основанная на использовании словаря [3], созданный Абрахамом Лемпелем, Якобом Зивом и Терри Велчем. Он был опубликован Велчем в 1984 году как улучшенная реализация алгоритма LZ78, опубликованного Лемпелем и Зивом в 1978 году. Алгоритм прост в реализации и может обеспечить очень высокую пропускную способность в аппаратных реализациях. Принцип работы алгоритма LZW:
- инициализация словаря: алгоритм начинается с инициализации словаря, который содержит все возможные односимвольные последовательности.
- чтение входных данных: алгоритм читает входные данные и ищет наиболее длинную строку, которая уже есть в словаре.
- вывод кода: когда найдена такая строка, алгоритм выводит код, соответствующий этой строке, и добавляет новую строку (найденную строку плюс следующий символ) в словарь.
- повторение процесса: этот процесс повторяется до тех пор, пока не будут прочитаны все входные данные.
- декодирование: для восстановления исходных данных из сжатого формата используется словарь, который строится декодером параллельно с кодированием.
Алгоритм LZW широко используется в формате изображений GIF и, опционально, в PDF и TIFF2. Он также является алгоритмом, используемым в утилите сжатия файлов Unix compress1. Основная идея алгоритма заключается в использовании повторяющихся шаблонов для экономии места при хранении данных. LZW является одним из основных методов сжатия данных общего назначения благодаря своей простоте и универсальности.
- Алгоритм Deflate – это алгоритм сжатия данных без потерь, который использует комбинацию двух других алгоритмов: LZ77 и кодирования Хаффмана. Он был разработан Филом Кацем для архиватора PKZIP и определён в спецификации RFC 19511. Работа алгоритма Deflate заключается в следующих этапах:
- сжатие LZ77: на первом этапе алгоритм ищет повторяющиеся последовательности в исходных данных и заменяет их ссылками на предыдущие вхождения этих последовательностей. Это позволяет уменьшить размер данных за счёт использования указателей на повторяющиеся фрагменты.
- кодирование Хаффмана: на втором этапе алгоритм применяет кодирование Хаффмана для дальнейшего сжатия данных. Символы, которые встречаются чаще, кодируются более короткими кодами, а редкие символы – более длинными.
- формат потока данных: поток данных Deflate состоит из серии блоков, каждый из которых начинается с трёхбитового заголовка. Заголовок указывает, является ли блок последним, и каким методом были закодированы данные (не закодированы, статический Хаффман или динамический Хаффман).
- декомпрессия: для восстановления исходных данных из сжатого формата используется обратный процесс декомпрессии, который интерпретирует сжатые данные с помощью построенных таблиц кодирования.
Алгоритм Deflate используется во многих форматах и протоколах, включая ZIP, gzip, PNG и другие. Он обеспечивает хорошее соотношение степени сжатия и скорости работы, что делает его популярным выбором для сжатия данных. Deflate считается свободным от патентов, что также способствовало его широкому распространению.
В целом, каждый из этих алгоритмов может быть использован для сжатия изображений без потерь, в зависимости от требований к сжатию данных. Выбор конкретного алгоритма зависит от многих факторов, таких как тип изображения, требования к качеству, скорость сжатия и объем памяти. Использование этих алгоритмов может значительно уменьшить размер файлов изображений, что уменьшает время передачи данных и уменьшает затраты на хранение данных.





