ИССЛЕДОВАНИЕ УКЛОНЕНИЯ ОТВЕСНОЙ ЛИНИИ НА ТЕРРИТОРИИ АСТРОНОМИЧЕСКОЙ ОБСЕРВАТОРИИ ИМЕНИ ЭНГЕЛЬГАРДТА

Уклонение отвесной линии

УОЛ (Уклонение Отвесной Линии)– угол между реальным направлением отвесной линии и нормалью к референц- эллипсоиду. Эта величина имеет две составляющие: в плоскости меридиана север- юг (ξ) и в плоскости первого вертикала восток- запад (η).

                                                                                                 (1),

α- геодезический азимут. [1]

Так как линейный базис обсерватории имени Энгельгардта расположен вдоль линии меридиана, можно найти только меридиональную составляющую (север- юг) уклонения отвесной линии.

                                                                                                           (2)

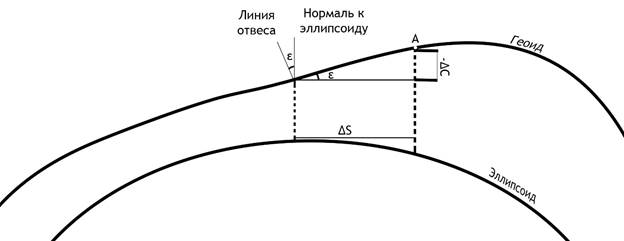
Рисунок 1. УОЛ и высота геоида

На рис.1 видно, что 

                                                                                                               (3).

∆S- горизонтальное проложение.

Через формулы 3 и 4 получаем:

                                                                                                        (4);

                                                                                                            (5).

То есть для того, чтобы посчитать меридиональную составляющую уклонения отвесной линии, необходимо знать разность высотных аномалий пары точек, горизонтальное проложение и азимут с пункта, на который ведется расчет этой величины.

Для расчета меридиональной составляющей уклонения отвесной линии использовались данные геометрического и спутникового нивелирования, а также дальномерные измерения, выполненные в период с 2012 по 2019 гг.

В качестве результата расчетов на рис.2 представлена динамика изменения уклонения отвесной линии на одном из пунктов линейного базиса.

Рисунок 2. Динамика ξ пункта 1

Оценка точности расчета меридиональной составляющей уклонения отвесной линии

Известно, что квадрат среднеквадратической ошибки (СКО) некоторой функции, например, трех аргументов вычисляется по формуле:

Для функции

                                                                                                         (6)

квадрат СКО равен

                                                                             (7)

Дифференцируя исходную формулу (6) для вычисления составляющей УОЛ в меридиане, имеем:

                                                                                                      (8)

                                                                                       (9)

Далее переходим к СКО составляющей УОЛ в меридиане:

                                                                                          (10)

 Так как   

                                                                                                          (11)

в итоге получаем в секундах дуги: 

                                                                                             (12).

По результатам оценки точности можно сделать вывод о том, что расстояние между пунктами существенно влияет на СКО, а именно, чем меньше горизонтальное проложение, тем выше ошибка. На этом основании, было принято следующее решение: для расчета ξ на конкретном не использовать данные, полученные на соседних или близлежащих пилонах.

В качестве итога можно сказать следующее:

• Постоянство ежегодных приращений ξ в течение нескольких лет на пунктах 1, 2, 3, 4 свидетельствует о возможном наличии общей волны наклона квазигеоида;
• Положение поверхности квазигеоида является более устойчивой его характеристикой, нежели наклон. По этой причине, изменение наклона обладает преимущественной геодинамической информативностью по сравнению с аномалией высоты.