ХЛОР ҚОСПАСЫНЫҢ СУДА ТАРАЛУЫН MAPLE ҚОЛДАНБАЛЫ ПАКЕТ НЕГІЗІНДЕ МАТЕМАТИКАЛЫҚ МОДЕЛЬДЕУ

Түйіндеме. Қазіргі уақытта білім беруде MathCAD, Maple, MАTLАB Mathematica және т.б. типті математикалық модельдерді құруға арналған бағдарламалық орталар кеңінен қолданылады. Осы аталған бағдарламалық орталарда хлор примесінің суда таралуын модельдеу шешімдері Maple бағдарламасын қолдана отырып графикалық әдіспен қарастырылады.

Аннотация. В настоящее время в образовании широко используются программные среды для построения математических моделей типа MathCAD, Maple, MАTLАB Mathematica и др. Решения по моделированию распределения хлора в воде в указанных программных средах рассматриваются графическим методом с использованием программы Maple.

Кілт сөздер. Математикалық пакеттер, модельдеу, бағдарлама, Maple.

Қазіргі таңда ғылым мен техниканың қарқынды дамуы жүріп жатқандықтан, біз жаңа технологияларды және  әртүрлі тиімді бағдарламаларды меңгеруіміз қажет.

ХХ ғасырдағы ғылыми техникалық революцияның нәтижесінде модельдеу әрекеттері қарқынды дами бастады. Жаңа компьютерлік жүйелердің пайда болу нәтижесінде модельдеудің жаңа құрушы программалары қалыптаса бастады.

Физика, математика және информатика бағыты бойынша білім алатын студенттер үшін математикалық немесе компьютерлік модельдеу әрекеттері меңгеру маңызды орын алады. ХХ ғасырдың 50 жылдары амалдарды электронды түрде орындайтын программаларды физика, математика, информатика мамандары кеңінен пайдалана бастады. Негізінен бұл әдіспен жауабы жоқ күрделі есептерді немесе аналитикалық жауабы жоқ есептердің шешілу жолдарын қарастырды. Тарихи фактілерге сүйенер болсақ, 1955 жылы Лос-Аламостың математик мамандары Энрико Фермиге тапсырма берген болатын. Аталмыш тапсырма 3 талапқа сай келу керек болды. Бірінші, талап аталмыш программаның информатиктердің қызығушылығын ояту мәселесі; екінші, талап аналитикалық шешімі болмауын қадағалау; үшінші, талап сол уақыттағы ЭЕМ - ге бәсеке тудыру.

Модельдеу – бір объектінің қасиеттерін зерттеу әдісі, зерттеуге қолайлырақ және бірінші объектімен белгілі бір сәйкестікте болатын басқа объектінің қасиеттерін зерттеу болып саналды. Модельдеу кезінде зерттеу объектінің өзімен емес, модель деп аталатын оның алмастырғышымен тәжірибе жасайды. Математикалық модельдеу – сыртқы орта әрекеттерінің математикалық белгілер арқылы берілуін айтамыз. Математикалық модельлерді дұрым меңгеру үшн ең әуелі сыртқы және ішкі ортаның әсерлерін игеруіміз маңызды рөл атқарады. Математикалық символдар мен белгілеулер жүйелерінің көмегімен өрнектелген және қарастырылатын объектінің кейбір қасиеттерін қамтып көрсететін осындай ұғымдар мен қатынастар жиынтығы қарастырылатын объект математикалық модель деп аталады.

Математикалық модельдеу арқылы жұмыс жасап отырған ғалым не студент зерттеліп жатқан объектіні және математикалық модельдеудің барлық қырларын біліп отыру қажет.

Математикалық модельдеу де 3-ке бөлінеді.

1. Аналитикалық модельдеу – нақты объектінің формализациясы мен оның шешімдерінің аналитикалық функцияларын анықтау.

2. Сандық модельдеу – математикалық модельдің аналитикалық шешімі болмаған жағдайда қолданылады. Берілген теңдеудің шешімін табу үшін итерационалды әдістер пайдаланылады.

3. Имитациялық модельдеу – күрделі жүйелер мен процестерді шешу барысында модель-имитатор енгізу. Әдетте экономикалық, өндірістік, экологиялық және басқа да процестерде қолданылады.

Осы математикалық модельдеудің хлор қоспасының суда таралуын қарастырайық.

Мәселелнің қойылуы. Хлор примесінің суда таралуын модельдеу қарастырайық.

                                                                                      (1)

Шешу әдісі.Тейлор қатарынада бірінші теңдікті ашамыз:

                                                                                        (2)

Теңдеудегі  бұл айырымдық сұлбасы, ал қалған  «туындын жуықтау қателігі» деп аталады.

Екінші теңдікті ашамыз:

                                                                                (3)

Үшінші теңдікті ашамыз:

                                                                                    (4)

Тейлор қатарына жайылған теңдеуді жинақтаймыз:

                                                              (5)

Теңдеуді шешу ұшін сандық әдістердің «Айдау әдісін» қолданамыз. Бұл жерде (5) теңдеуді түрлендіріп төмендегі түрге келтіреміз.

                                                                                                            (6)

Симмертриялық формуланы қолдана отырып "артқа" бойынша, сандық формуласын қолдана отырып, теңдеудің орына (j+1) тордың қабаты үшін (1) келесі айырмашылық теңдеуі болады.

                                                                                             (7)

                                                                                     (8)

Мұндағы:

Шекаралық шарттарды аламыз:

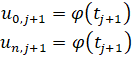                                                                                                          (9)

(8)-(9) жүйесін қуыу әдісімен шешетін боламыз.

                                                                                        (10)

Демек:

                                                                                  (11)

(11) өрнегін (8) формулаға алмастыра отырып.Осы түрге келтіреміз:

                                                                                        (12)

                                                                                      (13)

                                                                                                  (14)

                                                                                       (15)

I=1 кезінде, формулалардан:

                                                                                   (16)

                                                                                     (17)

Осы жерден шекаралық шарттарды қолдана отырып, біз аламыз:

                                                                                               (18)

(17) және (18) формулалары бірдей болуы керек болғандықтан, оларды салыстыра отырып, мына түрде аламыз:

                                                                                      (19)

                                                                               (20)

                                                                             (21)

Белгілеулер кірітеміз:

                                                                                                             (22)

                                                                                                        (23)

                                                                                                           (24)

                                                                                                           (25)

Белгілеулер кірітеміз, яғни:

                                                                                       (26)

Сонымен қатар (1) тендеудің және (26) тендеудің жалпы шешімі төмендегі көріністе болады:

Мaple қолданбалы пакет программа орталығындағы алынған негізгі шешімдер:

Сурет 1. Хлор қоспасының суда таралуын Maple қолданбалы пакет негізінде математикалық модельдеу

Алынған нәтижеге талдау.Бұл жердегі Maple бағдарламасына толығырақ тоқталып өтсек. MAPLE – көпшілік пайдаланушыларға арналған компьютерлік математикалық жүйе. Көпке дейін оны компьютерлік алгебра деп келді, себебі бұл бағларлама таңбалық есептеулерді, түрлендірулерді жүзеге мінсіз асырып келді. Алайда бұл атау аталмыш жүйенің қолданылу аясын тарылтып келді, шын мәнінде бұл жұйе басқа да командаларды, соның ішінде таңбалық, сандық есептерді ғана емес, басқа да визуалды графикалық электрондық құжаттарды жылдам әрі тиімді орындай алады.

Қорытынды.Дербес компьютерде жұмыс жасау арқылы математикадан көптеген есептерді шешу және автоматтандыру арқылы жеңілдетуге болады.Соңғы жылдардағы математика саласындағы  есептерді шешуде және математиканы оқытуда қолданылатын компьютерлік бағдарламалар дамуда. Математикалық есептерді шешу барысында Maple, MatLAB, Mathematica, MathCAD тәрізді  бағдарламаларды қолдана аламыз. Математиканы оқытуда компьютерлік бағдарламаларды қолдану маңыздылығына келетін болсақ символды турде алу, графигін сызып көрсету, анмациялық графиктарды салу тағыда басқалар болып табылады.