ОСНОВНЫЕ ЭТАПЫ МАТЕМАТИЧЕСКОГО МОДЕЛИРОВАНИЯ

Математическое моделирование – это исследование явлений, процессов, систем или объектов путем построения и изучения их моделей и использования последних для определения или уточнения характеристик и рациональных способов построения вновь конструируемых технологических процессов, систем и объектов. [2, с. 10]

Процесс моделирования в самом общем виде состоит из трех стадий перехода:

− формализация (переход от реального объекта к модели),

− моделирование (изучение, исследование и преобразование модели),

− интерпретация (перевод результатов моделирования из виртуальной, модельной области в реальную область).

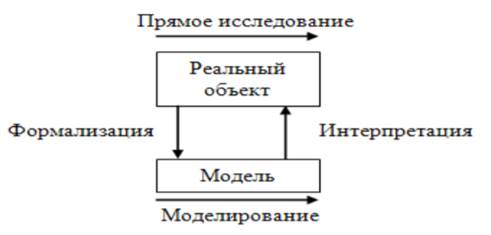
Рисунок 1. Основные стадии математического моделирования

1-я стадия (формализации) включает:

1) формирование предмета и цели исследования;

2) выделение элементов, соответствующих цели исследования, и их наиболее важных характеристик;

3) вербальное (словесное) описание взаимосвязей между элементами;

4) на этом этапе проводятся, статистические опросы, ставятся цели, используются планы, генерируются и подвергаются экспертизе идеи. Для генерации идей используются такие методы, как морфологический анализ, генетические алгоритмы, алгоритм изобретений, мозговой штурм, и др.

5) функциональное моделирование, т.е. введение символических обозначений для характеристик, установление общих закономерностей и количественных зависимостей. При функциональном моделировании для классификации элементов используются кластерный или многофакторный анализ, для установления общих закономерностей и зависимостей используются дисперсионный и корреляционный анализ;

6) выбор типа математической модели (алгебраическая линейная или нелинейная, дифференциальная и т.д.), вида модели (структуры, таблицы, векторы, матрицы, размерности и т.д.), приемов и методов моделирования (какие преобразования используются, например, Чебышева, Лапласа, симплексный, разностный и т.д.), формирование взаимосвязей между элементами с использованием математического аппарата.

2-я стадия (моделирования) включает:

1) проведение расчетов;

2) решение задачи анализа (исследование) – получение ответов на вопросы «что?, где?, когда?, почему?, что будет, если?». На этом этапе определяются характеристики системы, дополнительные условия, коэффициенты, прогнозные значения, исследуются устойчивость, чувствительность, управляемость и т.д.;

3) решение задачи синтеза (оптимизации). На этом этапе вносятся вид целевого показателя, независимые переменные, ограничения, возмущения, выбирается метод синтеза (вид программирования), определяются системные характеристики (показатели эффективности, область решений, наилучшие решения и параметры и т.д.).

3-я стадия включает реализацию способов интерпретации (истолкование, объяснение, перевод на более понятный естественный язык):

1) визуализация моделей и результатов моделирования, т.е. графическое отображение, использование блок-схем (чертежей, электрических схем, логических схем, графиков, таблиц, манипуляторов) [1, с. 21];

2) создание интерактивных моделей (позволяющих менять условия, параметры «на ходу» и наблюдать изменение модели);

3) статистические выводы, сглаживание и фильтрация результатов, создание программы действий, и т.д.

Процесс моделирования цикличен и имеет спиралевидный характер, то есть возможность возвращения с каждого этапа на более ранний этап при обнаружении ошибки. На рисунке 2 [1, с. 22] представлены основные этапы построения модели.

Рисунок 2. Этапы построения математической модели

Первые этапы решают менее формализованные задачи, последующие — все более формальные. Соответственно, методы первых этапов менее формализованы, а методы последующих – более формальные, мощные. Это означает, что самые трудные и ответственные этапы – первые, где требуется больше интуитивных решений. Ошибка на более ранних этапах больше сказывается на дальнейших решениях, возвращаться и переделывать приходится гораздо больше, чем на последних этапах. Поэтому к первым этапам проявляется повышенное внимание. Поскольку формальные методы легко автоматизируются, то последние этапы (4 – 7) поддержаны программными продуктами и легко доступны конечным пользователям. В сложных системах модель лишь частично отражает реальный процесс, поэтому необходима проверка степени соответствия (адекватности) модели и реального процесса. Проверка и корректировка модели, а также реализация найденного решения на практике выполняются на 5-м и 7-м этапах. Проверку производят сравнением предсказанного поведения с фактическим. Корректировка может потребовать дополнительных исследований объекта, уточнения структуры модели, изменения переменных. Тогда этапы моделирования повторяются, пока не будет достигнуто удовлетворительное соответствие между выходами объекта и модели. При этом цикл имеет вид спирали модернизации модели – с каждым повтором модель становится лучше, более детальной, а уровень ее описания – точнее.